Определение и снижение гидравлического сопротивления имеет большое значение при фильтрации жидкости в пористой среде. В статье делается попытка определения гидравлического сопротивления в слоисто-неоднородных пластах.
Ключевые слова: гидравлическое сопротивление, слоисто-неоднородный, фильтрация жидкости, среднее значение, проницаемость.
The determination and reduction of hydraulic resistance is of great importance when filtering a fluid in a porous medium. The article attempts to determine the hydraulic resistance in layered heterogeneous formations.
Key words: hydraulic resistance, layered heterogeneous, fluid filtration, average value, permeability.
Пористая среда называется неоднородной, если ее фильтрационные характеристики — проницаемость и пористость — различны в разных областях.
Однако часто изменение проницаемости по пласту носит столь хаотичный характер, что значительные области пласта можно считать в среднем однородно проницаемыми. Характеристики фильтрационных потоков в таких пластах с большой точностью отвечают характеристикам потоков, установленных в предыдущем параграфе для строго однородных пластов.
Но нередко встречаются такие пласты, значительные области которых сильно отличаются друг от друга по фильтрационным характеристикам. Это так называемые макро неоднородные пласты, параметры которых существенно влияют на характеристики фильтрационных потоков.
В пластах — коллекторах нефти и газа выделяют следующие основные виды макронеоднородности.
Слоистая неоднородность, когда пласт разделяется по толщине на несколько слоев, в каждом из которых проницаемость в среднем постоянна, но отлична от проницаемости соседних слоев. Такие пласты называют также неоднородными по толщине. Вследствие малости кривизны границы раздела между слоями с различными проницаемостями считают обычно плоскими. Таким образом, в модели слоистой пористой среды предполагается, что проницаемость изменяется только по толщине пласта и является кусочно-постоянной функцией вертикальной координаты. При этом можно считать, что пропластки разделены непроницаемыми границами (случай гидравлически изолированных слоев), либо учитывать перетоки между слоями с различными проницаемостями (случай гидродинамически сообщающихся пропластков).
В первом случае возможен расчет фильтрационных характеристик по одномерным моделям течения. Во втором случае точный учет перетоков флюида между пропластками требует решения двумерных задач фильтрации.
Предположим что, установившийся плоскорадиальный приток несжимаемой жидкости по закону Дарси направлен к гидродинамической совершенной скважине радиуса ![]() в слоисто-неоднородном пласте, состоящей из двух пропластков с разными толщинами и проницаемостями. При этом на контуре питания
в слоисто-неоднородном пласте, состоящей из двух пропластков с разными толщинами и проницаемостями. При этом на контуре питания ![]() и на забое скважины
и на забое скважины ![]() поддерживаются постоянными давления
поддерживаются постоянными давления ![]() и
и ![]() .
.
В каждом пропластке при его постоянной толщине ![]() и проницаемости
и проницаемости ![]()
![]() будет плоскорадиальное движение, а закон распределения давления в каждом из них описывается [1;2] уравнением:
будет плоскорадиальное движение, а закон распределения давления в каждом из них описывается [1;2] уравнением:
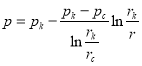 (1)
(1)
Скорость фильтрации пропорциональная проницаемости, будет в каждом пропластке иметь свое значение:
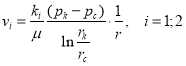 (2)
(2)
Как известно в пластовых условиях число Рейнольдса определяется формулой ![]() . Тогда
. Тогда ![]() . Учитывая формулы
. Учитывая формулы ![]() , эффективный диаметр
, эффективный диаметр ![]() и формулу (2) для гидравлического сопротивления получаем следующие формулы:
и формулу (2) для гидравлического сопротивления получаем следующие формулы:
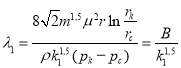 (3)
(3)
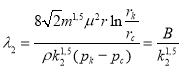 (4)
(4)
где 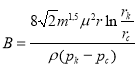 (5)
(5)
Дебит потока ![]() можно определить как сумму дебитов в отдельных пропластках,
можно определить как сумму дебитов в отдельных пропластках, ![]() .
.
Здесь
![]() ,
, ![]() (6)
(6)
где
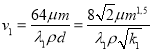 (7)
(7)
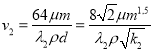 (8)
(8)
Тогда ![]() (9)
(9)
Среднее значение проницаемости пласта ![]() можно определить из равенства дебитов в реально неоднородных и эквиваленто однородном пластах:
можно определить из равенства дебитов в реально неоднородных и эквиваленто однородном пластах:
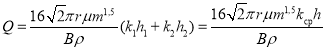 (10)
(10)
где ![]()
Из (10) получаем известную [1] формулу:
![]() (11)
(11)
А теперь определив
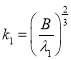 ,
, 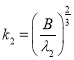 ,
, 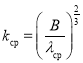
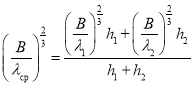
или 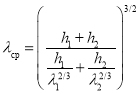 (12)
(12)
Если в формулу (2) подставим ![]() то получим
то получим ![]() , что и следовало ожидать.
, что и следовало ожидать.
Таким образом, мы получили формулы для гидравлических сопротивлений в слоисто-неоднородных пластах.
Литература:
- Подземная гидравлика. Учебник для вузов./ К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов.-М.:Недра, 1986–303 с.
- Чарный И. А. Подземная гидрогазодинамика. М.: Гостоптехиздат, 1963.







