В статье рассматривается расчет параметров чувствительного элемента упругого подвеса микромеханического гироскопа.Приводятся расчетные формулы для нахождения собственных часто в режиме движения и в режиме чувствительности.
Ключевые слова: микромеханический гироскоп, чувствительный элемент, упругий подвес, собственная частота, жесткость.
В начале XXI века основными критериями, которым должны отвечать современные устройства, стали мобильность, универсальность, компактность малая стоимость, но при этом важными остаются такие показатели как, энергопотребление, время готовности, диапазон измерений, точность. На рынки гражданской микроэлектроники наиболее востребованными становятся «умные» устройства, в которых свое применения находят микромеханические датчики. Следует отметить, что и в военной промышленности все чаще ведутся разговоры об «умном» оружие. И если уже несколько десятилетий военная техника оснащается сложными и дорогими навигационными системами, то сегодня речь идет о малогабаритных системах. В соответствии с новым трендом разработка микромеханические гироскопы (ММГ) являются перспективным направлением.
ММГ представляет собой объёмные многослойные микроструктуры, изготовленные из кристаллического материала, рабочие процессы в которых поддерживаются электроникой, выполненной по планарной технологии на одном или нескольких из слоев микроструктуры. Наиболее распространенными являются ММГ, работающие по принципу вибрационного гироскопа. Область применения данных гироскопов определяется классом точности. Столь малые размеры, которые составляют порядка нескольких миллиметров приводят к появлению определенных проблем, которые затрудняют повышение их точностных характеристик, а также накладывают ограничения на возможность использования в некоторых областях техники, работающих в жестких условиях.
Таким образом в настоящее время уделяется большое внимание проблеме совершенствования ММГ, изготовленных по кремневой технологии МЭМС. Рассмотрим последовательность расчета параметров чувствительного элемента (ЧЭ) ММГ RR-типа для эффективного функционирования в навигационных устройствах. Возможности технологий позволяют получать габариты датчиков RR -типа в плане 3.5 х 3.5 мм. В то же время существуют приемлемые размеры (ЧЭ) ММГ RR-типа, диаметр ротора которого может составлять до 20 мм. При этом предъявляются более высокие требования к их характеристикам. Толщина ротора обычно не более 60 мкм. При изготовлении таких чувствительных элементов (ЧЭ) необходимо использовать технологии фотолитографии и травления. Нами рассматривается возможность формирования ЧЭ толщиной, равной 40 мкм. Большая толщина ЧЭ вместе с большим диаметром увеличивают момент Кориолисовых сил. Данные обстоятельства способствуют повышению точности измерительного устройства [1].
Для проведения расчета создадим ЧЭ ММГ RR-типа который представлен на рис.1.
Конфигурация ЧМ гироскопа, включает в себя ротор 1, недеформируемые 4 и деформируемые 2,3 элементы подвеса, с анкером 5 и окошками 6 для установки ДМ и ДУ вытравленные в кремниевой пластине. С помощью анкера ЧЭ соединен с подложкой (основанием), а основание соединено c верхний крышкой на которой расположены электроды емкостного преобразователя перемещений, а также статорные элементы гребенчатой структуры электростатического привода (на рисунке 4 не показаны). Последние совмещено с роторными структурами, расположенными на роторе, создают вибрационный вращающий момент вокруг оси Z. Две пары упругих элементов 2 обеспечивают соединение ротора с недеформируемыми элементами 4, которые предполагаются абсолютно жесткими, а две пары упругих элементов 3 осуществляют соединение элементов подвеса 4 с анкером 5.
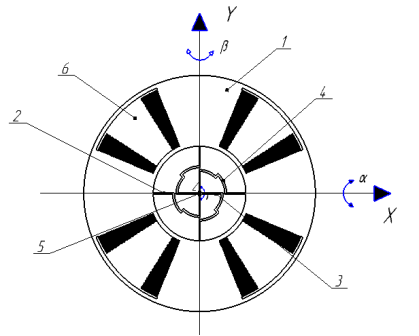
Рис. 1. Чувствительный элемент ММГ RR-типа: 1-ротор; 2,3- деформируемые элементы подвеса; 4- недеформируемые элементы подвеса; 5- анкер; 6- окошки для установки ДМ и ДУ
При повороте ротора вокруг оси X все упругие элементы, расположенные вдоль нее, работают на кручение, а размещенные вдоль оси Y, это так называемый режим чувствительности РЧ. При повороте вдоль оси Y элементы функционируют аналогично. При развороте ротора вокруг оси Z все упругие элементы подвергаются деформации изгиба, режим движения РД.
При появлении переносных угловых скоростей (корпуса) 
и 
, которые для гироскопа являются прецессией режим РЧ, возникает, переменны момент сил инерции Кориолиса, вызывающие колебания ротора по перекрестным осям. На рис. 2 приведена схема подвеса ЧЭ.
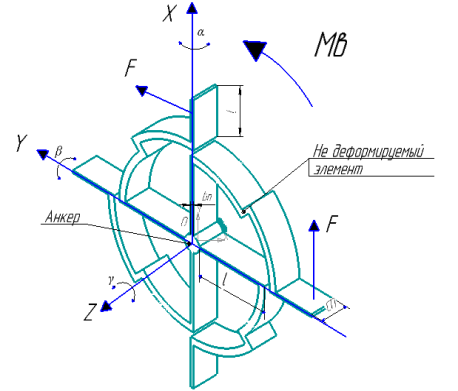
Рис. 2. Упругий подвес чувствительного элемента
Для определения параметров ЧЭ рассмотрим зависимость кинетического момента от размера ротора. Формула определения кинетического момента для ММГ RR-типа [2]:
(1)
где 
— момент инерции ротора, 
— амплитуда колебаний,
— собственная частота.
Полагаем, что ЧЭ выполнен из кремния со следующими параметрами:
Исходя из размеров ЧЭ ММГ по данным в работе [1], примем диаметр ротора до 10 мм, а толщину 40 мкм.
Получены следующие результаты зависимости кинетического момента от геометрических параметров ротора, которые представлены на рис 3.
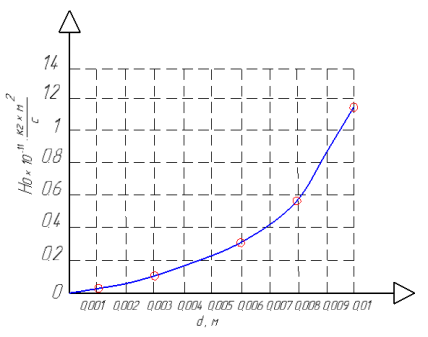
Рис. 3. Зависимость кинетического момента от геометрических параметров ротора
Из рис. 3 следует: увеличение размеров ЧЭ ММГ приводит к увеличению кинетического момента. Кроме того, зависимость имеет нелинейный характер.
Для расчета упругого подвеса приведенного на рис. 2 примем толщину упругого подвеса 
исходя из толщины ротора. Ширину будем выбирать в пределах 0,008–0,03 мм, исходя из жесткости упругих подвесов. Длиной упругих подвесов будем варьировать от половины диаметра ротора для обеспечения приближения к минимальной границе частоты собственных колебаний ротора в диапазоне ω = 3 кГц (данное значение берется из условия работы привода) [3].
Необходимую жесткость для создания частоты первичных колебаний можно выразить из формулы [2]:
(2)
где — момент инерции ротора; ω — собственная частота колебаний ротора; 
Для диаметра ЧЭ в 3 мм момент инерции ротора будет равен
(расчет был произведен в программе SolidWorks)
Далее варьируем геометрическими размерами упругого подвеса для достижения желаемой жесткости. Для рис. 2 можно считать, что при работе гироскопа деформируются только упругие элементы длиной l, которых в подвесе 8 штук. Для PД по координате γ можно принять схему заделки концов упругих элементов и нагружения, как на рис. 4.
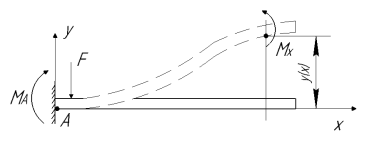
Рис. 4. Схема нагружения и деформации упругого элемента
Таким образом, полагая, что внутренние концы торсионов имеют жесткую связь с анкером, а силы приложены к наружным концам, которые «свободны» за счет вращательного движения ротора. ЧЭ гироскопа совершает колебания по координате γ (режим движения РД) и все упругие элементы подвеса работают на изгиб. Когда торсионы находятся внутри ротора, как на рис.5 и перемещение конца находится на расстоянии R от центра вращения, жесткость на изгиб каждого элемента относительно оси Z можно вычислить по формуле [4].
(3)
где 
– модуль сдвига кремния; l — длина торсиона;N — количество изгибов торсиона (N=1); R- радиус от центра до конца упругого элемента;
Имея в виду, что 
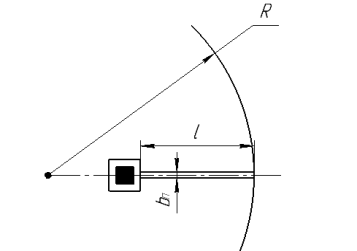
Рис. 5. Расчетная схема жесткости на изгиб относительно оси Z
Для последовательного соединения двух упругих элементов их жесткость равна 
, а так как пар, работающих параллельно, в подвесе 4 шт., то суммарная жесткость подвеса РД 
.Частота собственных колебаний определяется по формуле (2).
В режиме чувствительности (РЧ) в общем случи при колебании ротора по координате α или β упругие элементы вдоль одной оси подвергаются деформации кручения (рис.6), а подругой — деформации изгиба (рис.4). Предполагая, что каждая торсионная балка является прямой с постоянным поперечным сечением, и конструкционный материал является однородным и изотропным; жесткость на кручение каждой балки длиной l может быть определена по формуле (4) [4].
(4)
где S — площадь поперечного сечения; G — модуль сдвига кремния;
l — длина торсиона
Для балки с прямоугольным поперечным сечением шириной 
и толщиной 
учитывая, что 
площадь поперечного сечения коэффициент S может быть выражена по формуле 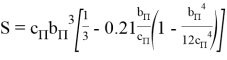(5)
(5)
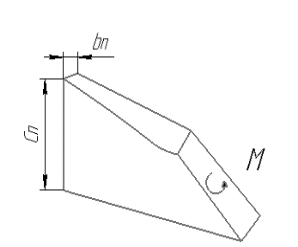
Рис. 6. Деформация упругого элемента на кручения вдоль оси Х или Y
Жесткость на изгиб может быть вычислена как
(6)
Суммарная жесткость на кручение и на изгиб по координате α или β:
Частота собственных колебаний определяется как
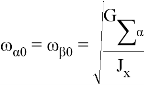
где 
экваториальный момент инерции ротора и упругих элементов относительно выходной оси;
Как показывают наши расчеты при принятых ограничениях на размер чувствительного элемента возможно реализовать конструкцию ЧЭ ММГ, при которой обеспечивается необходимая его чувствительность к входному сигналу. При этом можно выбрать систему возбуждения колебаний ротора способную обеспечить его движения на частоте 3кГц, с учетом жесткости подвесов.
Выводы:
При принятых ограничениях на размер чувствительного элемента возможно реализовать данную конструкцию, обеспечив необходимую резонансную частоту РД и РЧ.
Расчетные формулы позволяют произвести расчет конструкции, чувствительного элемента ММГ RR-типа, представленного в данной работе или аналогичного ей.
Задаваясь необходимыми геометрическими параметрами упругих элементов, можно добиться желаемой частоты собственных колебаний.
Литература:
- Коновалов С. Ф., Подчезерцев В. П., Майоров Д. В., Понамарев Ю. А. Двухкоординатный микромеханический ДУС с магнитоэлектрическими датчиками обратной связи по каналам возбуждения и измерения. — Гироскопия и навигация.2010. № 3 (70). С 61–71.
- Распопов В. Я. Микромеханические приборы: учебное пособие.--- М.: Машиностроение, 2007. –400с.
- Васильев А., Борисов Е. Производство МЭМС. Перспективы и решения. Электроника: Наука, технология, бизнес. 2012. № 3. С.60–65.
- Cenk Acar, Andrei Shkel Вибрационные гироскопы — 2008. — 280с
