В статье рассмотрены возможности применения принципа Даламбера и элементов теории удара при проектировании подвижных и раздвижных сопел ракетных двигателей твёрдого топлива.
Ключевые слова: механическая система, ракетный двигатель, ударная сила.
Работа ракетного двигателя твердого топлива (РДТТ) (рис. 1) представляет собой множество взаимосвязанных процессов различной природы. Как станет видно дальше, методы теоретической механики позволяют достаточно хорошо описывать некоторые из них. В данной работе рассмотрены методы теоретической механики применительно к различным конструкциям сопловых блоков РДТТ.
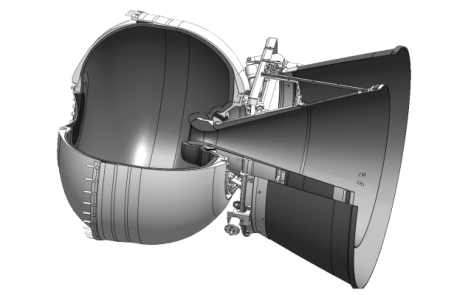
Рис. 1. Ракетный двигатель твёрдого топлива [2, c. 11]
Сопловой блок — один из основных элементов РДТТ, во многом определяющий его облик и энергомассовое совершенство. Он предназначен для создания тяги путём превращения тепловой энергии, выделяющейся при сгорании топлива, в кинетическую энергию продуктов сгорания; кроме того, он используется для управления вектором тяги по направлению.
1. Подвижное управляющее сопло
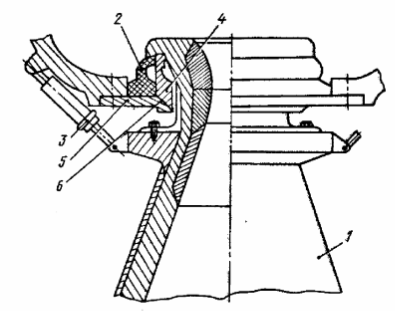
Рис. 2. Поворотное сопло на упругой основе
1 — сопловой блок; 2 — упругая опора; 3 — сервопривод; 4, 5 — пластина и переходное кольцо; 6 — узел крепления сервопривода
В настоящее время широкое распространение получили поворотные (качающиеся) сопла (рис. 2), в которых управляющее боковое усилие обеспечивается поворотом сопла.
При больших габаритных размерах сопла велики управляющие усилия, что ухудшает быстродействие узла регулирования и увеличивает массу узлов управления. В данном случае движение сопла может быть описано с помощью принципа Даламбера [1, c. 469] для механической системы, который гласит «в любой момент времени для движущейся точки сумма активных сил, реакций связей и силы инерции равна нолю”:
![]()
![]() , где
, где
– ![]() — главный вектор сил инерции;
— главный вектор сил инерции;
– ![]() — главный вектор реакции связей;
— главный вектор реакции связей;
– ![]() — главный вектор внешних сил;
— главный вектор внешних сил;
– ![]() — главный момент внешних сил;
— главный момент внешних сил;
– ![]() — главный момент реакции связей;
— главный момент реакции связей;
– ![]() — главный момент сил инерции.
— главный момент сил инерции.
Таким образом, если в любой момент времени к каждой из точек системы кроме действующих на неё внешних и внутренних сил, и реакций связей присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной и к ней можно применять все уравнения статики.
Решение этой системы уравнений позволит установить необходимый диапазон усилий, создаваемых сервоприводом, и затем перейти к минимизации его массы, в чём и заключается основная задача при проектировании поворотного управляющего сопла РДТТ.
2. Раздвижное сопло
Показателем эффективности ракетного двигателя в целом является величина, которая называется удельный импульс ![]() , где
, где ![]() тяга двигателя, а
тяга двигателя, а ![]() — секундный массовый расход.
— секундный массовый расход.
Есть реальная возможность увеличения удельного импульса высотной ступени ракеты путём увеличения геометрической степени расширения сопла ![]() , где
, где ![]() — диаметр среза сопла,
— диаметр среза сопла, ![]() — диаметр критического сечения сопла.
— диаметр критического сечения сопла.
Существует несколько реализаций увеличения геометрической степени расширения сопла во время полёта ракеты. Одним из таких способов являются раздвижные сопла (рис. 3).
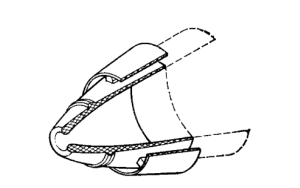
Рис. 3. Конструктивная схема сопла с переменной степенью расширения с жестким выдвигаемым насадком [2, c. 137]
Выдвижение насадков (или насадка) сопла производится по команде от системы управления. Команда подаётся на разрывной элемент (например, пироболт) узла фиксации, выдвигаемого насадка в исходном положении. После расфиксации происходит страгивание и выдвижение насадка под действием сил привода, а также сил, действующих в натурных условиях. Для обеспечения работоспособности конструкции необходимо обеспечить минимальные возмущающие воздействие на изделие при выдвижении и фиксации насадков.
Описать взаимодействие насадка с соплом и показать влияние этого процесса на работу двигателя в целом позволяет теория удара [1, с. 653].
Ударом называют явление, при котором за очень малый промежуток времени скорости точек тела изменяются на конечную величину. Ударная сила ![]() может достигать значительной величины. Импульс ударной силы называется ударным импульсом и является конечной величиной:
может достигать значительной величины. Импульс ударной силы называется ударным импульсом и является конечной величиной:
![]() ,
,
где
В теории удара применяют теорему об изменении количества движения материальной точки: изменение количества движения материальной точки за время удара равно действующему на эту точку ударному импульсу:
![]() ,
,
где ![]() — масса точки,
— масса точки, ![]() — скорость точки до удара,
— скорость точки до удара, ![]() — скорость точки после удара.
— скорость точки после удара.
Для механической системы, состоящей из n точек, это уравнение можно представить в виде:
![]() ,
,
где ![]() — масса
— масса ![]() -й точки,
-й точки, ![]() и
и ![]() — скорости k-й точки соответственно до и после удара,
— скорости k-й точки соответственно до и после удара, ![]() — равнодействующая всех внешних ударных импульсов, приложенных к k-й точке.
— равнодействующая всех внешних ударных импульсов, приложенных к k-й точке.
Теорема об изменении количества движения механической системы при ударе звучит так: изменение количества движения механической системы за время удара равно геометрической сумме всех внешних ударных импульсов, действующих на эту систему.
Уравнение для механической системы можно переписать в виде:
![]() ,
,
где ![]() — масса всей системы,
— масса всей системы, ![]() и
и ![]() — скорости центров масс системы соответственно в начале и в конце удара.
— скорости центров масс системы соответственно в начале и в конце удара.
Таким образом, по приведенным выше уравнениям можно рассчитать силу, которая будет действовать на сопловой насадок во время выдвижения. Это соответственно будет накладывать ограничения на допустимую скорость процесса, определять требования надежности конструкции насадка и выдвижного механизма и прочности для материала насадка.
Кроме того, пользуясь законом сохранения количества движения, можно будет учесть потери характеристической скорости ![]() (скорости Циолковского) в процессе выдвижении сопла, что особенно важно на верхних ступенях ракеты-носителя для вывода полезной нагрузки на заданную траекторию.
(скорости Циолковского) в процессе выдвижении сопла, что особенно важно на верхних ступенях ракеты-носителя для вывода полезной нагрузки на заданную траекторию.
Литература:
- Дронг В. И. и др. Курс теоретической механики/под ред // КС Колесникова, ВВ Дубинина. М.: Изд-во МГТУ им. НЭ Баумана. — 2011.
- Лавров Л. Н. и др. Конструкции ракетных двигателей на твердом топливе //М.: Машиностроение. — 1993.
- Ягодников Д. А., Ирьянов Н. Я. Ракетные двигательные установки. Термины и определения //Москва, Изд-во МГТУ им. НЭ Баумана. — 2012.







