Рассмотрим подход, основанный на линеаризации, который позволяет свести общую задачу к задаче с линейными ограничениями. Использование линеаризации дает возможность применять методы линейного программирования либо для решения последовательности задач ЛП, либо для итеративного выполнения тех или иных операций симплекс-метода.
Метод основан на разложении нелинейной функции ![]() общего вида в ряд Тейлора до членов первого порядка в окрестности некоторой точки
общего вида в ряд Тейлора до членов первого порядка в окрестности некоторой точки ![]()
![]()
Член второго порядка малости ![]() почти всегда отбрасывается, и функция
почти всегда отбрасывается, и функция ![]() аппроксимируется в точке
аппроксимируется в точке ![]() линейной функцией, обозначаемой следующим образом:
линейной функцией, обозначаемой следующим образом:
![]()
Точка ![]() называется точкой линеаризации. Следует иметь в виду что линеаризацию следует использовать с большой осторожностью поскольку в большинстве случаев она дает весьма грубое приближение. Тем не менее такое приближение часто применяется как при оптимизации, так и для других целей.
называется точкой линеаризации. Следует иметь в виду что линеаризацию следует использовать с большой осторожностью поскольку в большинстве случаев она дает весьма грубое приближение. Тем не менее такое приближение часто применяется как при оптимизации, так и для других целей.
Непосредственное использование последовательности задач ЛП
Наиболее простым способом линеаризации является замена общей нелинейной задачи на задачу, получаемую при помощи линеаризации всех функций, фигурирующих в исходной задаче. Поскольку при этом функции, входящие в задачу, заменяются на линейные, получается задача ЛП, которую можно решать при помощи методов ЛП. Очевидно, что получаемое таким образом решения является лишь некоторым приближением к решению исходной задачи: тем не менее, если принять меры предосторожности, найденное значение целевой функции будет лучше значения в точке линеаризации. Сначала рассматривается задача с линейными ограничениями и описываются дополнительные вычисления, необходимые для обеспечения эффективной непосредственной линеаризации. Затем рассматривается общая задача нелинейного программирования (НЛП).
Случай линейных ограничений
Задача НЛП с линейными ограничениями имеет следующий вид:
При ограничениях ![]()
Она отличается от задачи ЛП в стандартной форме нелинейностью целевой функции ![]() . Так же как для задачи ЛП, допустимая область является многогранником, т. е. геометрическим телом, образованным пересечением полуплоскостей. Поскольку функция
. Так же как для задачи ЛП, допустимая область является многогранником, т. е. геометрическим телом, образованным пересечением полуплоскостей. Поскольку функция ![]() нелинейная, оптимальное решением может не совпадать с вершиной или угловой точкой допустимой области. Кроме того, если
нелинейная, оптимальное решением может не совпадать с вершиной или угловой точкой допустимой области. Кроме того, если ![]() не выпуклая, задача НЛП с линейными ограничениями может иметь несколько локальных минимумов. Рассмотрим с учетом этих особенностей последовательность действий при формулировке и решении линеаризованной в некоторой допустимой точке
не выпуклая, задача НЛП с линейными ограничениями может иметь несколько локальных минимумов. Рассмотрим с учетом этих особенностей последовательность действий при формулировке и решении линеаризованной в некоторой допустимой точке ![]() задачи НЛП с линейными ограничениями.
задачи НЛП с линейными ограничениями.
Ясно, что задача вида:
![]()
При ограничениях ![]()
Представляет собой задачу ЛП и поэтому имеет оптимальное решение в допустимой угловой точке (при условии, что допустимая область ограничена). Весьма важен вопрос о соотношении между решением линеаризованной задачи ![]() и решением исходной задачи
и решением исходной задачи ![]() . Заметим, что при решении линеаризованной задачи получается единственное решение (если не принимать во внимание случай не единственности оптимума в задаче ЛП), тогда как исходная задача может иметь несколько локальных экстремумов. Выбор точки локального экстремума в близи
. Заметим, что при решении линеаризованной задачи получается единственное решение (если не принимать во внимание случай не единственности оптимума в задаче ЛП), тогда как исходная задача может иметь несколько локальных экстремумов. Выбор точки локального экстремума в близи ![]() зависит от выбора начальной точки линеаризации. Следовательно, при невыпуклой целевой функции нельзя быть уверенным в том, что найдено приближение к глобальному экстремуму. Однако даже в случае выпуклой функции
зависит от выбора начальной точки линеаризации. Следовательно, при невыпуклой целевой функции нельзя быть уверенным в том, что найдено приближение к глобальному экстремуму. Однако даже в случае выпуклой функции ![]() нет гарантии, что точка
нет гарантии, что точка ![]() хорошо «приближает»
хорошо «приближает» ![]() . Истинное решение
. Истинное решение ![]() может лежать внутри допустимой области, а точка
может лежать внутри допустимой области, а точка ![]() должна быть угловой. Из этого следует, что и в случае выпуклой функции
должна быть угловой. Из этого следует, что и в случае выпуклой функции ![]() для получения хорошего приближенного решения
для получения хорошего приближенного решения ![]() необходима дополнительная корректировка
необходима дополнительная корректировка ![]() .
.
Заметим, что в силу допустимости точек ![]() ,
,![]() имеет место неравенство
имеет место неравенство
![]()
Следовательно, если воспользоваться формулой для ![]() , то получается следующее неравенство:
, то получается следующее неравенство:
![]() или
или ![]()
Очевидно, что вектор
![]()
Следовательно, решение задачи ЛП, не дающее хорошего приближения к оптимуму, позволяет получить важную информацию: определить направление поиска и точку пересечения соответствующего луча с границей допустимой области.
В результате решения задачи
![]()
Находится допустимая точка ![]() , такая, что
, такая, что
![]()
Поскольку величина ![]() вообще не равна нулю, полученная точка
вообще не равна нулю, полученная точка ![]() может служить точкой линеаризации для построения следующей аппроксимации. Решение последовательности задач ЛП и одномерный поиск продолжаются до тех пор, пока последовательные оптимумы
может служить точкой линеаризации для построения следующей аппроксимации. Решение последовательности задач ЛП и одномерный поиск продолжаются до тех пор, пока последовательные оптимумы ![]() , получаемые при помощи одномерного поиска, не станут достаточно близкими (т. е. расстояние между ними не станет меньше заранее выбранной малой величины).
, получаемые при помощи одномерного поиска, не станут достаточно близкими (т. е. расстояние между ними не станет меньше заранее выбранной малой величины).
Далее рассмотрим соответствующий алгоритм Франка-Вульфа.
Алгоритм Франка-Вульфа
Рассмотрим итерационный процесс:
Существует целевая функция
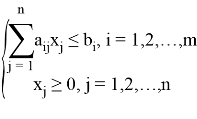
Пусть ![]() начальное приближение целевой функции, удовлетворяющее заданные ограничения.
начальное приближение целевой функции, удовлетворяющее заданные ограничения.
Найдём вектор градиент целевой функции в точке начального приближения.
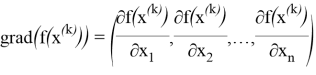
Составим новую линейную целевую функцию, которую нужно максимизировать (минимизировать).
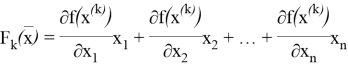
Заметим, что данную оптимизационную задачу, заданную нелинейной целевой функции, мы свели к решению задачи линейного программирования.
Решая задачу линейного программирования с учетом заданных ограничений, находим точку оптимума ![]() .
.
Новое приближение находится следующим образом:
![]()
Где
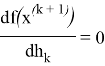
Если уравнение имеет не единственный корень, то за ![]() принимают наименьший корень.
принимают наименьший корень.
Условие выхода из итерационного процесса: ![]() или
или
![]() , где
, где ![]()
Оптимизация многоступенчатого компрессора
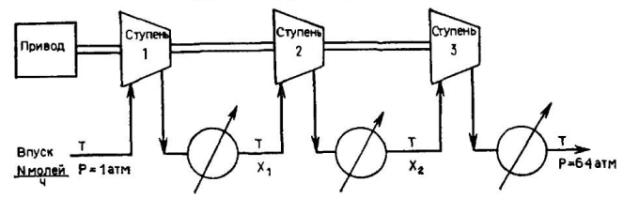 Рис. 1
Рис. 1
Изображенный на рис. 1 трехступенчатый компрессор предназначен для сжатия газа, поступающего под давлением 1 атм. в количестве ![]() моль/ч, до давления 64 атм. Предполагается, что сжатие двустороннее и адиабатическое; после каждой его стадии газ охлаждается до начальной температуры
моль/ч, до давления 64 атм. Предполагается, что сжатие двустороннее и адиабатическое; после каждой его стадии газ охлаждается до начальной температуры ![]() Требуется выбрать значения давления на промежуточных стадиях процесса,
Требуется выбрать значения давления на промежуточных стадиях процесса, ![]() потребление энергии.
потребление энергии.
Решение: Для двустороннего адиабатического сжатия с охлаждением до начальной температуры ![]() работа газа задается формулой
работа газа задается формулой
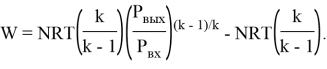
Где ![]() коэффициент Пуассона,
коэффициент Пуассона, ![]() универсальная газовая постоянная.
универсальная газовая постоянная.
При трехступенчатом сжатии полная работа газа определяется формулой
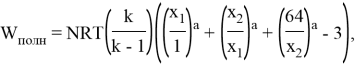
Где ![]() ,
, ![]() выходное давление на первой ступени,
выходное давление на первой ступени, ![]() выходное давление на второй ступени.
выходное давление на второй ступени.
Если для рассматриваемого газа ![]() , то при фиксированных
, то при фиксированных ![]() и
и ![]() оптимальные давления
оптимальные давления ![]() и
и ![]() можно получить, решая следующую задачу:
можно получить, решая следующую задачу:
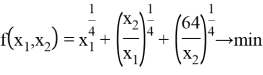
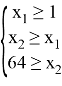
(при этом требуется, чтобы выбранные давления монотонно увеличивались от входа к выходу).
![]()
![]()
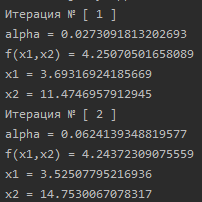
Можно заметить, что итерационный процесс алгоритма Франка-Вульфа прервался после второй итерации, не достигнув заданной точности.
Анализируя метод можно заметить, что при выборе шага
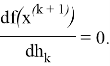
Оно может быть не обязательно дифференцируемо. Могут существовать разрывы 1-го и 2-го рода. Если оптимальное решение итерационного процесса не удовлетворяет условия заказчика, то следует исследовать данное уравнение на ![]() -ом шаге на гладкость и непрерывность, тем самым повысить точность алгоритма Франка-Вульфа.
-ом шаге на гладкость и непрерывность, тем самым повысить точность алгоритма Франка-Вульфа.
Рассмотрим график целевой функции на промежутке с учётом ограничений
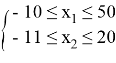
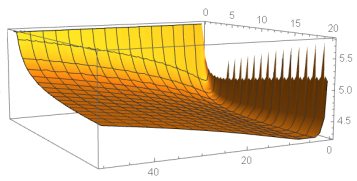
Функция монотонно возрастающая и имеет точки перегиба. Это объясняет трудность программного вычисления «самого» оптимального случая.
Литература:
- Пшеничный Б. Н., Данилин Ю. М. Численные методы в экстремальных задачах. М.: Наука, 1975. — 320с.
- Евтушенко Ю. Г. Методы решения экстремальных задач и их применение в системах оптимизации. М.: Наука, 1982. 432с.
- Химмельблау Д. Прикладное нелинейное программирование. М.: Мир, 1975. 536с.







