Точные методы решения задач теории фильтрации упругой жидкости довольно сложны. Указанные обстоятельства вызывают необходимость применения приближенных методов. В данной статье для решения задач теории фильтрации упругой жидкости предложен метод «усреднений» для второй фазы распределения давления в пласте.
Ключевые слова: начальный градиент, метод усреднений, неустановившийся, приближенный, распределение давления, вторая фаза.
Exact methods for solving problems of the theory of elastic fluid filtration are quite complex. These circumstances necessitate the use of approximate methods. In this article, the method of «averaging» for the second phase of the pressure distribution in the reservoir is proposed to solve the problems of the theory of elastic fluid filtration.
Keywords: initial gradient, averaging method, unsteady, approximate, pressure distribution, second phase.
Как известно дифференциальное уравнение неустановившегося течения жидкости в круговом пласте с учетом влияния начального градиента имеет вид:
(1)
где 
— радиус-вектор точки.
Заменим уравнение (1) приближенно уравнением
(2)
где
(3)
Предположим, что задано забойное давление и давление на контуре. Требуется определить перераспределение давления во второй фазе распределение давления в пласте с учетом влияния начального градиента давления [1,2]. Граничные условия для данного случая запишутся в следующем виде:
при 
(4)
при 
Решая уравнение (1), получаем:
(5)
Используя условия (4) при 
получаем:
(6)
при 
имеем:
(7)
Вычитая из (5) выражение (6), получаем:
(8)
Если вычесть из (6) выражение (7), то получаем:
(9)
Найдя 
из (9), получаем:
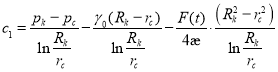(10)
Подставляя это выражение в (9), получаем:
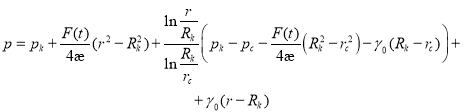(11)
Для определения 
на границе возмущенной части примем
при 
(12)
Из уравнения (11) имеем:
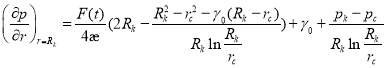(13)
На основании выражения (12), приравнивая уравнение (13) к нулю, определяем
:
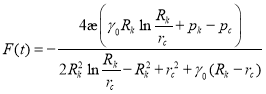(14)
Подставив выражение (14) в формулу (11) получаем:
Во второй фазе воронка депрессии доходит до непроницаемой границы, и на последней давление начинает падать. Поэтому в формулах необходимо учесть, что 
т. е. давление на контуре — переменная величина. Если из выражения (11) найдем 
и подставим в выражение (3) с учетом формулы (14), получим следующие выражения:
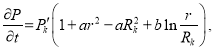(15)
где 
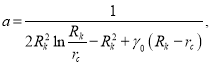
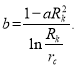(16)
Здесь и в дальнейшем при интегрировании членами 
(в связи их малости по отношению к 
) пренебрегают. Тогда имеем:
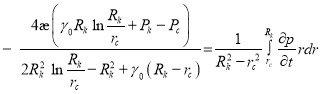(17)
или 
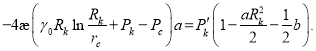(18)
Введя обозначение
(19)
после несложных преобразований получим дифференциальное уравнение:
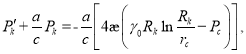(20)
откуда после его решения имеем:
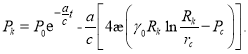(21)
Таким образом, мы получаем формулу для определения давления на контуре во времени во второй фазе распределение давления в пласте с учетом влияния начального градиента давления.
Литература:
- Г. П. Гусейнов. Некоторые вопросы гидродинамики нефтяного пласта. Азербайджанское государственное издательство. Баку -1961, 232 с.
- Подземная гидравлика. Учебник для вузов. К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов.-М.:Недра, 1986–303 с.
