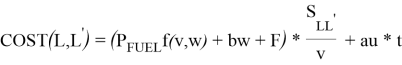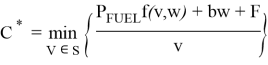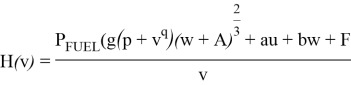Цель данной статьи — найти общие подходы для минимизации расходов с помощью нахождения оптимальной скорости судна при которой расходы и выбросы будут минимальны вне зависимости от сценариев маршрутизации, а также составление модели с помощью которой можно рассчитать оптимальную скорость для одного судна. Данная расчеты будут более правильны для танкеров, сухогрузов или небольших судов, так как для этих судов зависимость скорости и расхода топлива можно представить в виде кубической зависимости. И будет менее реалистичны для около нулевых скоростей других типов кораблей, таких как быстрые большие контейнерные судна.
Ключевые слова: оптимизация скорости судна; снижения расходов топлива.
Введение
Общая стоимость обычно составляет около 12–25 %, хотя стоимость топлива и масла намного выше для некоторых типов судов. Особенно, когда цены на топливо высоки, стоимость топлива является наиболее важной частью затрат на путешествие [1, C. 25].
Хотя технологии улучшаются день ото дня, затраты на топливо все еще остаются важными. Расходы на топливо варьируются в зависимости от типа двигателя судна, мощности машины, типа используемого топлива и цены за единицу топлива. Регулярное техническое обслуживание главного двигателя, обучение и опыт персонала, работающего в машинном отделении, являются другими важными факторами, влияющими на расход топлива [2, C.113].
Основные расходы, связанные с транспортировкой груза:
Стоимость топлива: поскольку во время чартера фрахтователь платит за топливо, главная задача для фрахтователя выяснить, должен ли он завершить поездку как можно скорее, так чтобы уменьшить чартер, выплачиваемый владельцу судна или идти медленнее, чтобы снизить стоимость топлива. Предполагается, что топливо покупается по известной цене топлива ![]() ($ / т). Сценарий по умолчанию игнорирует связанные с портом расходы, которые должны нести фрахтователь. Независимо от сценария, будь то фиксированный маршрут или гибкий маршрут, первое свойство заключается в том, что решение о скорости на каждом участке маршрута можно разложить по скорости и (если применимо) решения о маршрутизации на последующих участках маршрута.
($ / т). Сценарий по умолчанию игнорирует связанные с портом расходы, которые должны нести фрахтователь. Независимо от сценария, будь то фиксированный маршрут или гибкий маршрут, первое свойство заключается в том, что решение о скорости на каждом участке маршрута можно разложить по скорости и (если применимо) решения о маршрутизации на последующих участках маршрута.
Стоимость чартерного времени: в чартерном времени фрахтователь выплачивает владельцу судна известный тариф фрахта F ($ / день), F в основном определяется рыночными условиями.
Стоимость топлива корабля на стоянке: третий компонент стоимости, который мы принимаем как расход топлива на погрузке судна.
Методы ипринципы исследования
Реалистичная близкая форма для расчета расхода топлива, аппроксимация f учитывающая параметры скорость и загрузку:
|
|
(1) |
Где g> 0, p ≥ 0, q ≥ 3, и A — «вес легкого корабля», то есть вес судна, если оно пустое, включая топливо и другие расходные материалы. Обоснование такого формулировка такова, что расход топлива пропорционален смачиваемой поверхности корабля, которая пропорциональна водоизмещению корабля (w + A) возведенную в степень 2/3; Как сказано ранее, большинство работ в литературе предполагают кубическую функцию, то есть p = 0 и q = 3 и нет зависимости от полезной нагрузки.
Независимо от сценария, будь то фиксированный маршрут или гибкий маршрут, первое свойство заключается в том, что решение о скорости на каждом участке маршрута можно разложить по скорости и (если применимо) решения о маршрутизации на последующих участках маршрута. Глядя на конкретную часть маршрута, и предполагая, что судно находится в порту L и хочет плыть к следующему порт L ′, общая стоимость на участке (L, L ′) равна
|
|
(2) |
Где v скорость корабля во время этапа; w полезная нагрузка корабля во время этапа; u общий вес груза, который еще не собран, пока корабль плывет на маршруте; F стоимость сдачи в аренду судна; a неотрицательная константа, стоимость ожидания до загрузки груза; b неотрицательная константа стоимость перевозки товара; ![]() стоимость топлива; t время ожидания до загрузки. Эта стоимость может быть сведена к минимуму по отношению к скорости v. Как мы можем выделить расстояние до участка
стоимость топлива; t время ожидания до загрузки. Эта стоимость может быть сведена к минимуму по отношению к скорости v. Как мы можем выделить расстояние до участка ![]() , оптимальная скорость на участке является решением следующего уравнения:
, оптимальная скорость на участке является решением следующего уравнения:
|
|
(3) |
|
S = |
(4) |
![]() минимальная стоимость мили на участке пути. Оптимальная скорость корабля — это решение следующего уравнения, где скорость
минимальная стоимость мили на участке пути. Оптимальная скорость корабля — это решение следующего уравнения, где скорость ![]()
![]() минимальная стоимость мили. Так как
минимальная стоимость мили. Так как ![]() это
это ![]() )
)![]() . Нам нужно минимизировать функцию (5)
. Нам нужно минимизировать функцию (5)
|
|
(5) |
Для минимальных выбросов (или минимальной расхода топлива установим a=b=F=0 и добавим коэффициент CARB (выбросы/ т) топлива тогда функция примет вид
|
|
(6) |
Заключение
В этом исследовании мы нашли уравнения с помощью которого можно рассчитывать оптимальную скорость на участке. Отметим, что он не зависит расстояние ![]() .
. ![]() зависит от переменных w и u, которые зависят от всей истории маршрута судна до L, этот минимум за стоимость мили также не зависит ни от L, ни от L ', то есть не зависит от того, участок маршрута находится на рассмотрении.
зависит от переменных w и u, которые зависят от всей истории маршрута судна до L, этот минимум за стоимость мили также не зависит ни от L, ни от L ', то есть не зависит от того, участок маршрута находится на рассмотрении.
Литература:
- Alderton, P. M. (1981). The optimum speed of ship. The Journal of Navigation, 34(3), 341–355.
- Chrzanowski, I. (1989). An ıntroduction to shipping economics. United Kingdom.
- Barrass, C.B. (2005). Ship Design and Performance for Masters and Mates. Butterworth-Heinemann, UK.
- Bektas, T. and Laporte, G. (2011). The Pollution-Routing Problem. Transportation Research Part B 45 1232–1250.
- CBO (2006). The Economic Costs of Disruptions in Container Shipments, U. S. Congress, Congressional Budget Office, Washington, DC.
- Cariou, P., and Cheaitou, A., 2012. The effectiveness of a European speed limit versus an international bunker-levy to reduce CO2 emissions from container shipping. Transportation Research Part D, 17, 116–123.
- Cordeau, J.-F., Laporte, G., Legato P. and Moccia, L. (2005). Models and Tabu Search Heuristics for the Berth-Allocation Problem. Transportation Science 39(4), 526–538.
- Norstad, I., Fagerholt, K., Laporte, G., (2011). Tramp ship routing and scheduling with speed optimization. Transportation Research Part C 19, 853– 865.
- Psaraftis, H.N. (2011). A multi-commodity, capacitated pickup and delivery problem: The single and two-vehicle cases. European Journal of Operational Research 215, 572–580.
- Psaraftis, H.N., Kontovas, C.A. (2009). CO2 Emissions Statistics for the World Commercial Fleet. WMU Journal of Maritime Affairs,Vol. 8:1, 1–25