Разработка моделей для системы автоматизированного проектирования высокочастотных трансформаторов с сердечником из аморфной стали



Актуальность проблемы

В настоящее время в промышленности применяются различные электротехнические установки, работающие на повышенной частоте. К ним, в частности, можно отнести установки для индукционного нагрева деталей, сварочные инверторы, высокочастотные стабилизаторы напряжения и зарядные устройства. Повышенная частота, на которой работают данные устройства, позволяет повысить качество функционирования данных устройств и качество электромагнитного преобразования энергии. Например, сварочные инверторы в отличие от обычных аппаратов, работающих на частоте сетевого напряжения 50 Гц, используют ток высокой частоты (несколько десятков килогерц). С одной стороны, это позволяет получить более ровный шов. Диапазон регулировки сварочного тока оказывается более широким, что особенно важно при сварке тонкими электродами. Эта регулировка гораздо точнее и выходные параметры намного стабильнее, что сильно упрощает подбор оптимального режима работы. Зарядные устройства, работающие на повышенной частоте, обеспечивают меньшие пульсации напряжения выпрямленного тока. Использование повышенной частоты в стабилизаторах напряжения также позволяет получить лучшие характеристики, чем при использовании промышленной частоты 50 Гц.

Одним из немаловажных плюсов таких установок является уменьшенные габариты, что вызвано, в первую очередь, тем, что необходимым элементом подобных устройств является трансформатор, габариты которого во многом определяют и габариты всего устройства. Так как напряжение на обмотках трансформатора связана с амплитудным значением магнитного потока Ф_m отношением

,(1)

то с ростом частоты f при сохранении величины магнитной индукции B и при том же количестве витков обмотки w активное сечение стержней трансформатора S_a может быть уменьшено во столько же раз, во сколько увеличивается частота.

Проблема здесь состоит в том, что потери холостого хода трансформатора с ростом частоты растут в соответствии с соотношением

,(2)

где p — удельные потери в стали; m и n — коэффициенты, значения которых определяются эмпирическим путем для каждой марки стали.

Поэтому при традиционном исполнении трансформатора с ростом частоты приходится снижать магнитную индукцию, что приводит к росту габаритов. Однако если магнитопровод трансформатора изготавливается из ферромагнитных материалов с малыми удельными потерями p на высоких частотах, то его габариты удается существенно снизить.

В последнее время для данных целей все большее применение находят аморфные стали, толщиной 20–30 мкм, имеющие узкую петлю гистерезиса и низкую электропроводность, что позволяет существенно снизить магнитные потери как на гистерезис, так и на вихревые токи [1].

В состав аморфных ферромагнитных сплавов с беспорядочным расположением атомов входят две группы элементов: переходные металлы (Fe, Co) и аморфообразующие элементы — аморфизаторы (B, C, Si). Аморфная структура сплава получается только при определенной скорости его охлаждения — до десятков и даже сотен тысяч градусов в секунду.

В структуре аморфных сплавов отсутствует периодичность в расположении атомов. Несмотря на то, что плотность аморфных сплавов на 1–2 % ниже плотности кристаллических аналогов, прочность их выше в 5–10 раз [2], что связано с отсутствием вакансионно-подобных дефектов (дислокации и границы зерен, свойственные кристаллическому состоянию), имеющих вид узких щелей, в которых не может разместиться атом. Наличие таких дефектов сильно затрудняет диффузию через аморфные металлические слои.

Беспорядок расположения атомов в виде ближнего порядка оказывает сильное влияние на электропроводность аморфных сплавов. Их удельное электрическое сопротивление в 3–5 раз выше, чем у кристаллических аналогов. Это связано с тем, что при движении электронов через непостоянную структуру аморфной стали они испытывают гораздо больше столкновений с ионами, чем в кристаллической решетке.

Придание материалам специфических свойств (например, петля гистерезиса определенной формы) достигается термической или термомагнитной обработкой, в результате которой структура ленты может остаться аморфной, стать частично кристаллизованной или нанокристаллической [3].

Частичную кристаллизацию получают прерыванием процесса на начальной стадии термической обработки. Кристаллизованный материал занимает меньший объем, чем этот же материал с аморфной структурой, из-за плотной упаковки атомов. В результате поверхностные слои толщиной не более 1 мкм, в которых вырастают кристаллиты на начальной стадии, сжимают центральный слой ленты с аморфной структурой. Такая слоеная структура ленты (кристаллическая — аморфная — кристаллическая) обеспечивает линейность кривой намагничивания материала.

Магнитопроводы из аморфных и нанокристаллических сплавов по сравнению с электротехнической сталью имеют значительно меньшие удельные магнитные потери и высокую начальную и максимальную магнитную проницаемость и индукцию насыщения на высоких частотах.

Ввиду наличия специфических особенностей конструкции высокочастотных трансформаторов с сердечником из аморфной стали требуется особый подход к разработке математических моделей, заложенных в систему автоматизированного проектирования данных устройств.

Конструкция высокочастотного трансформатора

Высокочастотный трансформатор может быть реализован как в однофазном, так и в трехфазном исполнении. Рассмотрим пример конструкции масляного однофазного ВЧТ [4].

Технология навивки элементов магнитопровода из аморфной ленты оказывается достаточно трудоемкой. Поэтому данный процесс обычно осуществляется на заводе-изготовителе аморфной стали. На рис. 1 представлены варианты изготовления магнитной системы разных трансформаторов.

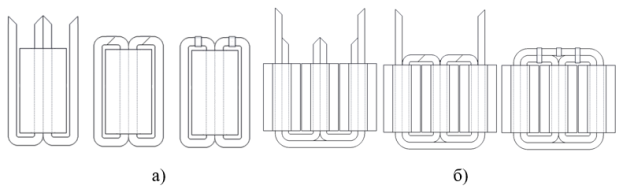
Рис. 1. Схема навивки магнитной системы и установки обмоток: а — однофазный трансформатор бронестержневой конструкции; б — трехфазный трансформатор стержневой конструкции

Витой элемент частично запекается в специальном лаке. Верхний стык расшихтовывается, а после установки обмоток вновь зашихтовывается и бандажируется. Обмотки наматываются специальный каркас (рис. 2,а).

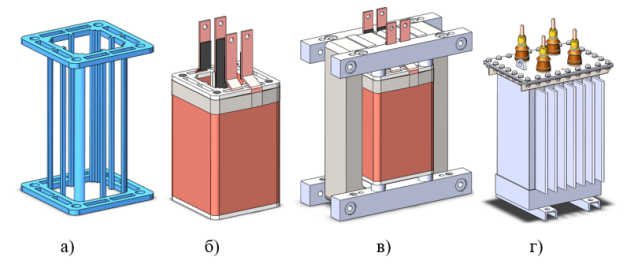
Рис. 2. Элементы конструкции ВЧТ

Блок обмоток имеет конструкцию, показанную на рис. 2,б. Конструкция активной части однофазного ВЧТ приведена на рис. 2,в. Для уменьшения потерь на вихревые токи нажимные балки выполняются из стеклотекстолита (в сухих ВЧТ) или дерева (в масляных ВЧТ). Масляный трансформатор в сборе представлен на рис. 2,г. Данный трансформатор имеет герметичное исполнение с гофробаком без расширителя.

Магнитопровод трехфазного трансформатора также рекомендуется изготавливать в бронестержневом исполнении из четырех витых колец из аморфной стали (по два кольца, различающихся длиной ярма). Однако возможен и вариант стержневой конструкции, представленный на рис. 1,б.

Особенности методики проектирования ВЧТ

Методика расчета параметров холостого хода может быть построена на основе конечно-элементной модели магнитного поля, которая автоматически строится по заданным размерам магнитной системы с помощью программного кода, обращающегося к соответствующим функциям генерации элементов модели, реализуемой библиотеки конечно-элементного моделирования EMLib (авторская разработка) [5] (рис. 3,а). При реализации САПР на основе пакета MSExcel (наиболее простой и эффективный способ реализации САПР ВЧТ) данный программный код пишется во встроенной системе программирования VBA.

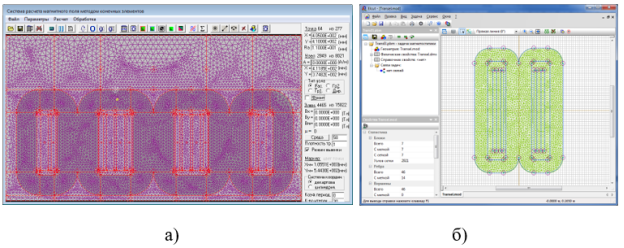
Рис. 3. Конечно-элементная модель магнитного поля трехфазного трансформатора в EMLib (а) и однофазного трансформатора в ELCUT (б)

Аналогичный функционал может быть реализован с использованием пакета ELCUT [6] в технологии ActiveField (рис. 3,б).

Серию расчетов магнитного поля при различных значениях тока холостого хода в первичной обмотке можно также реализовать в пакетном режиме с обращением к модели магнитного поля на каждом шаге. Для учета технологического зазора используется методика, предложенная в [7]. При этом кривая намагничивания стали магнитопровода приводится к виду B(H'). При этом расчетная напряженность магнитного поля в сердечнике с технологическим зазором рассчитывается по формуле

,(3)

где — расчетный коэффициент, учитывающий наличие технологического зазора; — относительная величина зазора; δ — расчетная величина зазора; L — длина средней силовой линии магнитопровода.

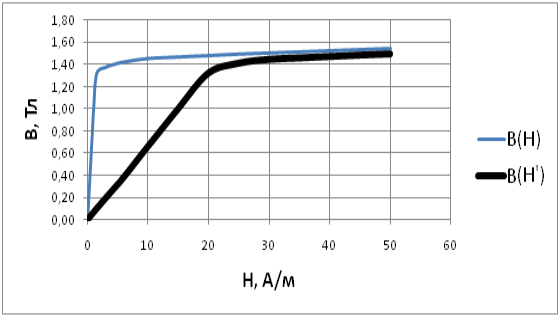
Рис. 4. Исходная табличная кривая B(H) (тонкая линия) и расчетная кривая B(H') (жирная линия)

Это значит, что для каждого i-го табличного значения индукции B_i реальной кривой намагничивания аморфной стали табличное значение H_i необходимо умножить на расчетный коэффициент K_i(μ), который в свою очередь зависит от магнитной проницаемости стали μ_i. Ввиду нелинейности коэффициента K(μ) расчет кривой B(H') по заданной табличной кривой B(H) для каждой i-й точки требует циклических операции по уточнению значений μ. Сравнение исходной табличной кривой B(H) и расчетной кривой B(H') приведено на рис. 4.

Для расчета тока холостого хода (ХХ) реализуется серия расчетов квазистационарного магнитного поля при варьировании тока в первичной обмотке в диапазоне 0 ≤ i₀ ≤ i_0.max, где i_0.max — некоторое максимальное амплитудное значение тока ХХ. По результатам данной серии расчетов строится кривая намагничивания трансформатора в форме Ф_m(i₀), по которой определяется ток ХХ, обеспечивающий значение Ф_m, соответствующее номинальному напряжению первичной обмотки в соответствии с отношением (1).

Для полученного таким образом значения тока ХХ рассчитывается магнитное поле в сердечнике трансформатора и по результатам данного расчета определяются потери ХХ путем суммирования потерь в каждом треугольном элементе конечно-элементной сетки по формуле

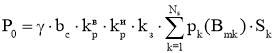,(4)

где γ — удельный вес аморфной стали; b_c — толщина магнитопровода в третьем измерении (сечение магнитопровода прямоугольное); — коэффициент увеличения потерь за счет действия остаточных механических напряжений в ленте; — коэффициент увеличения потерь за счет искажения формы кривой магнитной индукции; k_з — коэффициент заполнения стали; N_s — количество треугольных элементов конечно-элементной модели, заполненных сталью; S_k — площадь k-го элемента;.p — удельные потери в стали для заданной частоты при магнитной индукции B_m, Вт/кг.

В трехфазном трансформаторе ток в одной из обмоток ВН задается равным амплитудному значению тока холостого хода i₀, а в двух других фазах — равным половине амплитуды тока холостого хода с обратным знаком, то есть –i₀/2.

Упрощенный расчет параметров холостого хода можно осуществлять по результатам расчета магнитной цепи. При этом индукция в стержнях и ярмах магнитопровода бронестержневой конструкции однофазного трансформатора вычисляется по формуле

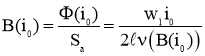, (5)

где — удельное магнитное сопротивления стали, рассчитанное по кривой намагничивания для индукции B(i₀); — длина средней линии витого кольца магнитопровода; w₁ — число витков в первичной обмотке;

Магнитная цепь рассчитывается в нелинейной постановке с итерационным уточнением значений для каждого значения тока i₀.

Магнитные цепи каждой фазы трехфазного трансформатора бронестержневой конструкции (рис. 1,а) можно считать независимыми друг от друга. В случае стержневой конструкции магнитопровода (рис. 1,а) магнитная цепь имеет вид, представленный на рис. 5. В этом случае значения Ф(i₀) для каждого стержня рассчитывается по методу контурных токов.

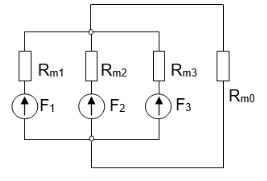
Рис. 5. Магнитная цепь трансформатора стержневой конструкции

Магнитные сопротивления стержней рассчитываются по формуле

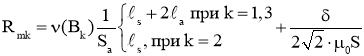,(6)

где – длина средней линии магнитного поля в стержне и в примыкающем к нему участке ярма; δ — расчетное значение технологического зазора между стержнем и ярмом; 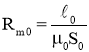— магнитное сопротивление нулевой последовательности; – длина средней линии и сечение магнитного поля нулевой последовательности; F_{k —} намагничивающая сила первичной обмотки на k-м стержне.

Параметры короткого замыкания можно рассчитать на основе расчета магнитного поля рассеяния. Фрагмент конечно-элементной модели магнитного поля рассеяния представлен на рис. 5. В данной модели полные токи в сечениях первичной и вторичной обмоток задаются одинаковыми (равными амплитудному значению намагничивающей силы первичной обмотки), но противоположными по направлению. Этим имитируется опыт короткого замыкания (КЗ) трансформатора. По рассчитанным при этом потоксцеплениям первичной и вторичной обмоток определяются индуктивности рассеяния

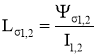.(7)

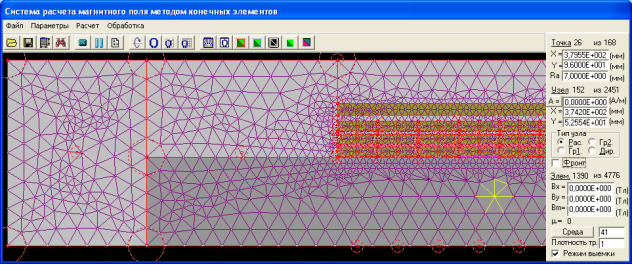
Рис. 6. Модель магнитного поля для расчета поля рассеяния трансформатора

При расчете активного сопротивления обмоток необходимо более внимательно подходить к учету влияния эффекта вытеснения тока на повышенной частоте. Для этого используется коэффициент добавочных потерь, вычисляемый по формуле 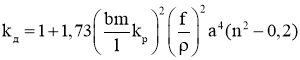[8]

, (8)

где m и n — число проводников обмотки соответственно в осевом и радиальном направлении; b и a — размер проводника соответственно в осевом и радиальном направлении, м; l — общий размер обмотки в осевом направлении, м; k_р — коэффициент приведения поля рассеяния (коэффициент Роговского; ρ — удельное электрическое сопротивление металла обмоток, мкОм·м.

Для учета эффекта вытеснения тока активные сопротивления обмоток, рассчитанные без учета данного эффекта, необходимо умножить на k_д.

В качестве расширенной подсистемы поверочного расчета в разработанной версии САПР ВЧТ используется модель произвольных режимов работы трансформатора, реализованная в MatLab Simulink SimPowerSystem, позволяющая осуществлять исследование рассчитанного варианта ВЧТ в режиме имитации эксперимента в реальном времени. На рис. 7 приведена динамическая модель однофазного трансформатора [9], а на рис. 8 — динамическая модель трехфазного трансформатора стержневой конструкции (трехфазный трансформатор бронестержневой конструкции может быть представлен обычной трансформаторной группой из трех однофазных трансформаторов).

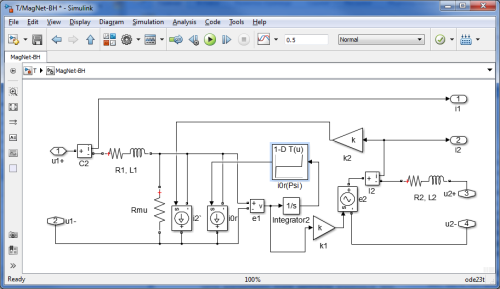
Рис. 7. Модель однофазного нелинейного трансформатора

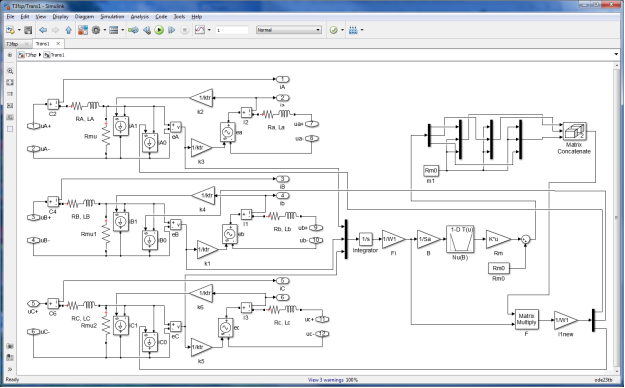
Рис. 8. Динамическая модель стержневого трехфазного трансформатора

Модель однофазного ВЧТ строится на основе идеального трансформатора с использованием регулируемого источника тока в первичной обмотке и регулируемого источника ЭДС во вторичной обмотке. Ветвь намагничивания представлена активным сопротивлением R_µ и регулируемым источником тока I_0r, величина которого определяется по кривой намагничивания в форме I_0r(Ψ₁), рассчитанной по результатам расчета либо магнитного поля, либо магнитной цепи (см. выше). При этом потокосцепление первичной обмотки определяется на каждом шаге интегрирования по времени по формуле

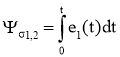.(8)

Величина сопротивления R_µ вычисляется по формуле

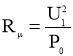.(9)

В модели трехфазного трансформатора стержневой конструкции (см. рис. 8) реактивные составляющие токов намагничивания фаз рассчитываются по формуле

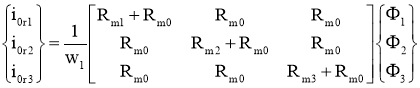.(10)

Для расчета магнитных сопротивлений стержней на каждом шаге интегрирования по времени используется формула (6).

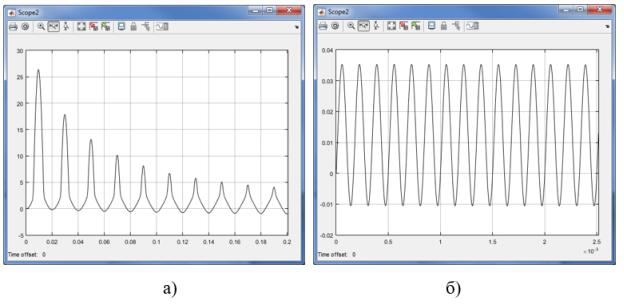
Рис. 9. Кривые тока первичной обмотки при включении однофазного трансформатора на ХХ: а — на частоте 50 Гц; б — на частоте 6 кГц

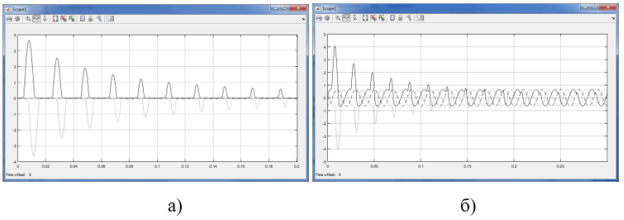
Рис. 10. Кривые тока первичной обмотки при включении трехфазного трансформатора на 50 Гц: а — на ХХ; б — на нагрузку

В качестве примеров функционирования разработанных моделей на рис. 9–10 приведены кривые включения однофазного и трехфазного трансформатора на ХХ и на нагрузку. Особенно интересны в плане теории кривые, полученные на 50 Гц, в которых присутствуют искажения, вызванные насыщением стали. При включении трансформатора на частоте 6000 Гц (рис. 9,б) такие искажения отсутствуют, что лишний раз свидетельствует о более высоком качестве процессов преобразования энергии в ВЧТ.

Полученные модели позволяют исследовать спроектированный трансформатора в разных режимах путем имитации эксперимента. Например, имитируя опыт короткого замыкания, можно получить определить напряжения короткого замыкания.

Выводы

Актуальность проблемы проектирования ВЧТ приводит к необходимости разработки моделей процессов, происходящих в трансформаторе на повышенной частоте. Предложена методика поверочного расчета, основанная на построении модели динамических режимов работы трансформатора с использованием имитационного пакета MatLab Simulink SimPowerSystem. Параметры данной модели вычисляются по уточненным методикам на основе расчета магнитного поля методом конечных элементов (для расчета параметров ХХ можно воспользоваться моделью магнитной цепи). Анализ результатов имитационного моделирования позволяет исследовать работу трансформатора в разных режимах, в том числе аварийных. Разработанные модели могут быть оформлены в качестве подсистем (блоков структурной схемы) и использованы в качестве элементов электрических цепей, в которые включены исследуемые трансформаторы. Это позволяет проанализировать работу спроектированного трансформатора непосредственно по месту установки.

Работа была выполнена при частичной финансовой поддержке РФФИ, региональный конкурс Ивановской области, проект № 18–43–370012 от 09.06.2018.

Литература:

1. Еремин И. В., Тихонов А.И, Попов Г. В. Проектирование силовых трансформаторов с сердечником из аморфной стали / ФГБОУВПО «Ивановский государственный энергетический университет имени В. И. Ленина». — Иваново, 2014. — 84 с.
2. Золотухин, И. В. Физические свойства аморфных металлических материалов / И. В. Золотухин. — М.: Металлургия, 1986. — 176 с.
3. ЧП Терейковский А. С. [Электронный ресурс] — www.ferrite.com.ua.
4. Тихонов А. И., Стулов А. В., Еремин И. В., Плаксин А. В. Разработка конструкции и методики проектирования высокочастотных трансформаторов с сердечником из аморфных сплавов. — Иваново: Вестник ИГЭУ, 2018, Вып. 6, с. 57–65.
5. Тихонов А. И., Булатов Л. Н. Платформонезависимая библиотека конечно-элементного моделирования магнитного поля / Свидетельство о государственной регистрации программы для ЭВМ. — М.: Федеральная служба по интеллектуальной собственности, патентам и товарным знакам. –№ 2011614852. Заявка № 2011613040, приоритет от 28.04.2011, Зарегистрировано в Реестре программ для ЭВМ 22.06.2011.
6. ELCUT: Моделирование двумерных полей методом конечных элементов. Версия 5.4: руководство пользователя. — Санкт-Петербург, Производственный кооператив ТОР, 2007. — 297с.
7. Тихонов А. И., Попов Г. В., Еремин И. В. Особенности методики расчета холостого хода трансформатора с сердечником из аморфной стали. — Иваново: «Вестник ИГЭУ», 2013, Вып. 4., с. 32–35.
8. Тихомиров П. М. Расчет трансформаторов: учеб. пособие для вузов. — 7-е изд. — М.: ЛЕЛАНД, 2014. — 528 с.
9. Тихонов А. И., Каржевин А. А., Подобный А. В., Дрязгов Д. Е. Разработка и исследование динамической модели однофазного трансформатора с сердечником из аморфной стали. — Иваново: «Вестник ИГЭУ», 2019. — Вып. 2, с. 59–70.