В статье авторы теоретически обосновывают явления нейронных сетей, описывают авторскую разработку, распознающую рукописные цифры нейронной сети.
Ключевые слова: сеть, нейронная сеть, искусственный интеллект, язык программирования, протон, python, сигмоида, входной слой, скрытый слой, выходной слой, функция активации, jupiter notebook.
Структура нейронной сети пришла в мир программирования из биологии. Благодаря структуре нейрона, машина обретает способность анализировать и даже запоминать различную информацию. Нейронные сети также способны не только анализировать входящую информацию, но и воспроизводить ее из своей памяти. Другими словами, нейросеть – это машинная интерпретация мозга человека, в котором находятся миллионы нейронов, передающих информацию в виде электрических импульсов.
Нейронные сети используются для решения сложных задач, которые требуют аналитических вычислений подобных тем, что делает человеческий мозг. Под нейроном мы будем понимать вычислительную единицу, которая получает информацию, производит над ней простые вычисления и передает ее дальше. Нейроны делятся на три основных типа: входной (input), скрытый (hidden) и выходной (output).
В том случае, когда нейросеть состоит из большого количества нейронов, вводят термин слоя. Соответственно, есть входной слой, который получает информацию, n скрытых слоев (обычно их не больше трех), которые ее обрабатывают и, выходной слой, который выводит результат. У каждого из нейронов есть два основных параметра: входные данные (input data) и выходные данные (output data). В случае входного нейрона: input=output. В остальных, в поле input попадает суммарная информация всех нейронов с предыдущего слоя, после чего, она нормализуется, с помощью функции активации.
Синапс – это связь между двумя нейронами. У синапсов есть один параметр — вес. Благодаря ему, входная информация изменяется, когда передается от одного нейрона к другому. Допустим, есть три нейрона, которые передают информацию следующему. Тогда у нас есть три веса, соответствующие каждому из этих нейронов. У того нейрона, у которого вес будет больше, та информация и будет доминирующей в следующем нейроне (пример — смешение цветов). На самом деле, совокупность весов нейронной сети или матрица весов — это своеобразный мозг всей системы. Именно благодаря этим весам, входная информация обрабатывается и превращается в результат.
Способ нормализации входных данных – это функция активации. То есть, если на входе у нас будет большое число, пропустив его через функцию активации, мы получим выход в нужном нам диапазоне. Функций активации достаточно много, но самые основные: Линейная, Сигмоид (Логистическая) и Гиперболический тангенс. Главные их отличия — это диапазон значений.
В данном примере используется сигмоида (рис. 1):
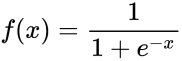
Рис. 1. Функция активации
Это самая распространенная функция активации, ее диапазон значений [0,1]. Именно на ней показано большинство примеров в сети, также ее иногда называют логистической функцией.
Чтобы обучить нейронную сеть используются два файла из базы данных MNIST, которая состоит из заранее подготовленных примеров изображений, на основе которых проводится обучение и тестирование систем. База данных была создана после переработки оригинального набора чёрно-белых образцов размером 20x20 пикселей NIST.
База данных MNIST содержит 60000 изображений для обучения и 10000 изображений для тестирования.
При расчете нейронной сети следует обратить внимание, что наша сетка состоит из 28х28=784 пикселей, пусть есть 784 нейрона, содержащие различные числа от 0 до 1: чем ближе пиксель к белому цвету, тем ближе соответствующее число к единице. Эти заполняющие сетку числа назовем активациями нейронов.
Описанные 784 нейрона образуют первый слой нейросети. Последний слой содержит 10 нейронов, каждый из которых соответствует одной из десяти цифр. В этих числах активация это также число от нуля до единицы, отражающее насколько система уверена, что входное изображение содержит соответствующую цифру.
Далееприступаем к написанию кода. Класс нашей нейронной сети должен состоять из:
– инициализации — задание количества входных, скрытых и выходных узлов;
– тренировки — уточнение весовых коэффициентов в процессе обработки предоставленных для обучения сети тренировочных примеров;
– опроса — получение значений сигналов с выходных узлов после предоставления значений входящих сигналов.
В таблице (табл. 1) приведены основные классы и методы, которые мнами используются и их краткое описание. Так же предоставлен список используемых библиотек.
В методе _init_ мы даем возможность самостоятельно задавать необходимое нам значения количества узлов во входном, скрытом и выходном слое (рис. 2), а также коэффициента обучения.
Таблица 1
Используемые классы, библиотеки и методы
|
Класс: |
||
|
neuralNetwork |
Основной класс, в котором идет разработка нейронной сети. |
|
|
Методы: |
||
|
_init_ |
Инициализирование нейронной сети. Задание количества узлов в слоях, задание функции активатора, коэффициента обучения и.т.д. |
|
|
Train |
Тренировка нейронной сети. Преобразовывание входных значений и поиск закономерностей. |
|
|
Query |
Опрос нейронной сети. |
|
|
Библиотеки |
||
|
Numpy |
Для работы с сложными матричными вычислениями. |
|
|
Matplotlib |
Построение графиков, визуализация данных. |
|
|
scipy.spesial |
Библиотека содержит необходимую функцию сигмоиды. |
|
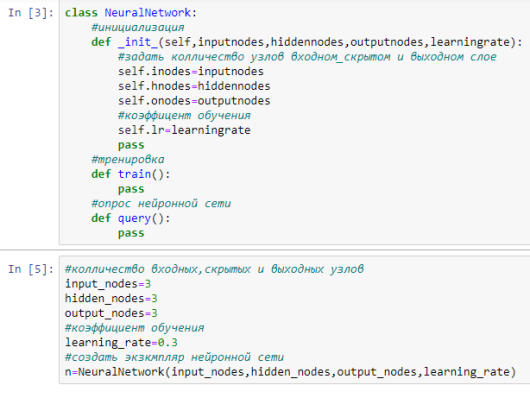
Рис. 2. Каркас нейронной сети
Дальше мы задаем веса. Наиболее важная часть этой сети — весовые коэффициенты связей (веса). Они используются для расчета распространения сигналов в прямом направлении, а также обратного распространения ошибок, и именно весовые коэффициенты уточняются в попытке улучшить характеристики сети [1, c. 161].
На данном этапе нами создан каркас, который позволит проверить начальную работоспособность нашей нейронной сети. Для этого создаем небольшую сеть, состоящую из трех входных, выходных и скрытых слоев c заданным коэффициентом обучения. Так мы проверяем, что на основе нашего каркаса подобную сеть можно создать. На рис. 3 приведен полный код метода _init_.
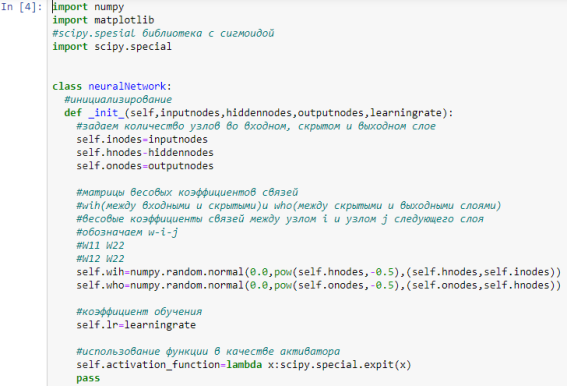
Рис. 3. Задание матриц весовых коэффициентов
Далее метод query () принимает в качестве аргумента входные данные нейронной сети и возвращает ее выходные данные (рис. 4).
Ниже показано, как можно получить входящие сигналы для узлов скрытого слоя путем сочетания матрицы весовых коэффициентов связей между входным и скрытым слоями с матрицей входных сигналов:
X скрытый= Wвходной скрытый • I
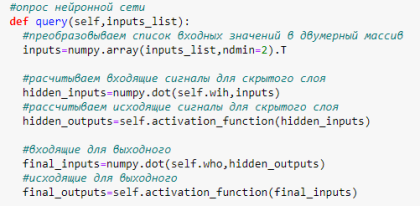
Рис. 4. Задание входных данных
Для получения же выходных сигналов скрытого слоя мы просто применяем к каждому из них сигмоиду:
Оскрытый = сигмоида (X скрытый)
Таким образом, сигналы, исходящие из скрытого слоя, описываются матрицей hidden_outputs, а входящие hidden_inputs.
Разработка метода train() (рис. 5) почти не отличается от метода query().
Единственным отличием является введение дополнительного параметра targets_list, передаваемого при вызове функции, поскольку невозможно тренировать сеть без предоставления ей тренировочных примеров, которые включают желаемые или целевые значения [1, с. 170]. Мы должны вычислить ошибку, являющуюся разностью между желаемым и целевым значением, предоставленным тренировочным примером. Она представляет собой разницу между матрицами (targets-final_outputs), рассчитываемую поэлементно.
На этом этапе с описанием класса нейронный сети можно закончить и приступить к описанию самой нейронной сети, на примере уже показанном на (рис. 5). Только заменяя значения на вычисленные и подключая необходимые базы данных.
На рисунке 6 показано как нами задаются 784 входных узла, 100 скрытых и 10 выходных. А также подключаются для построчного чтения файл “mnist_train.cvs”. Мы выбрали построчное чтение, так как данные о значениях пикселях и маркировок с правильными ответами для тренировки сети на каждую цифру вмещается в одну строку, притом, что первая цифра строки и есть маркер, являющийся ответом.
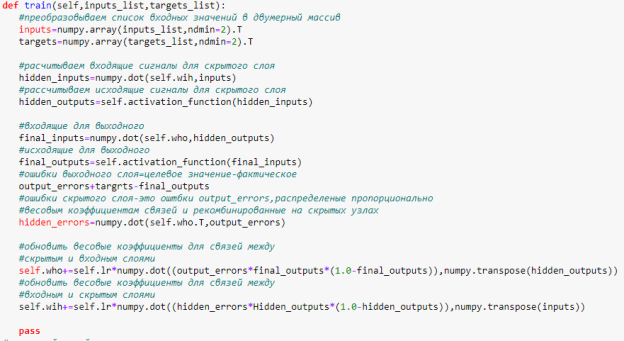
Рис. 5. Вычисление ошибок
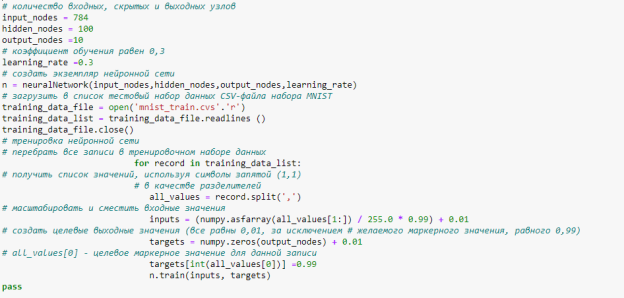
Рис. 6. Загрузка тестового набора
Прежде чем войти в цикл, обрабатывающий все записи тестового набора данных, мы создаем пустой список scorecard, который будет служить журналом оценок работы сети, обновляемым после обработки каждой записи. В цикле мы делаем то, что уже делали раньше: извлекаем значения из текстовой записи, в которой они разделены запятыми. Первое значение, указывающее правильный ответ, сохраняется в отдельной переменной. Остальные значения масштабируются, чтобы их можно было использовать в качестве входных данных для передачи запроса нейронной сети. Ответ нейронной сети сохраняется в переменной outputs [1, с. 196].

Рис.7. Подключение файлов
Для самого же тестирования нейронной сети нам необходимы файлы для тестировки, которые подключаются аналогично предыдущим (рис. 7).
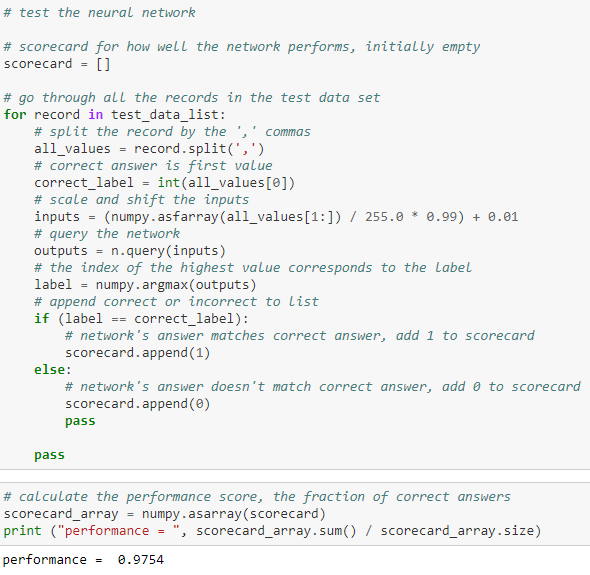
Рис. 8. Тестирование нейронной сети
В самом начале правильность распознавания составила почти 95. Дополним код фрагментом, который будет выводить относительную долю правильных ответов в виде дроби (рис. 8).
После улучшения кода, а именно: более точного определения коэффициента обучения и прогона через циклы, а также небольшого изменения конфигурации сети мы добились улучшения результата до 97.54%
Таким образом, подходящим языком программирования для разработки нейронной сети является язык программирования “Python”, по причине того, что он достаточно прост в изучении и читаемости кода, имеет обширное количество библиотек используемых для работы с базами данных и математическими вычислениями.
При выборе среды разработки для создания нейронной сети выбрана программа “JupiterNotebook”. Так как данная среда прекрасно подходит для обучения, имеющая довольно обширные возможности вплоть до параллельной визуализации данных по мере выполнения кода.
Литература:
- Рашид Т. Создаем нейронную сеть. Пер. с англ. – Спб. : ООО «Альфа-книга», 2017 – 272 с.







