Время перехода из нестационарного состояния в стационарное является одним из важных параметров, характеризующих процесс фильтрации газа в пористой среде. В данной статье сделана попытка определить это время.
Ключевые слова: установившийся, неустановившийся, время перехода, фильтрация, плоскорадиальный, gas.
The transition time from a non-stationary state to a stationary state is one of the important parameters that characterize the process of gas filtration in a porous medium. In this article an attempt is made to determine the time.
Keywords: steady-state, unsteady, transition time, filtration, plane-radial, gas.
При эксплуатации нефтяных, газовых и газоконденсатных месторождений с пуском скважин в эксплуатацию часто в пластах возникают неустановившиеся процессы, в связи, с чем дебит, скорость фильтрации, перераспределение давления изменяются во времени [1,2,3,4].
При постоянной депрессии неустановившаяся плоскорадиальная фильтрация после некоторого времени переходит в установившееся состояние. В этом случае перераспределение давления и скорость фильтрации в любой точке пласта будут зависеть только от расстояния данной точки от оси скважины.
Предположим, что горизонтальный газовый пласт радиусом контура питания 
, толщиной 
эксплуатируется скважиной радиусом 
. Под влиянием депрессии 
происходит фильтрация газа к скважине. При этом перепад давления 
тратится на преодоление сил трения, инерционных сил и на преодоление начального градиента давления (если он имеется). Тогда можно написать:
(1)
где 
— начальная депрессия, которую необходимо преодолеть; 
— депрессия, которая тратится на преодоление сил трения; 
— депрессия, которая тратится на преодоление сил инерции.
зависит от вязкости фильтрующегося газа, и ее можно определить по формуле Дюпюи:
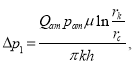(2)
где 
— вязкость газа; 
— дебит скважины; 
— проницаемость.
связано с влиянием инерционных сил и его можно определить по формуле:
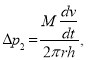
здесь
(3)
где 
— масса газа; 
— скорость фильтрации; 
— пористость.
Если учесть (2) и (3) в (1), то получается формула:
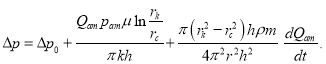(4)
После несложных преобразований формула (4) примет вид:
, (5)
где
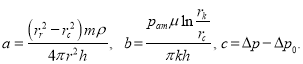
Решим дифференциальное уравнение (5) следующим образом.
Пусть 
(6)
Тогда уравнение (5) примет вид:
(7)
Если примем 
(8)
то получим 
(9)
или, интегрируя, получаем: 
где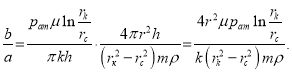 
(10)
Здесь 
— интегральная постоянная. Для определения А учтем, что при 
дебит 
Используя формулы (5), (6), (8) и (10), получаем:
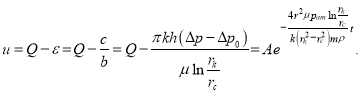(11)
Учитывая, что 
при 
, из (11) получаем
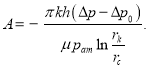(12)
Используя (11) и (12), для дебита скважины получаем формулу:
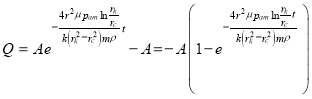
или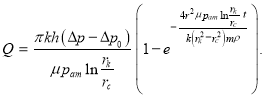 
(13)
Как видно из формулы (13), при 
мы получаем:
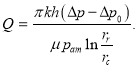(14)
То есть в этом случае инерционные силы теряют свое влияние на процесс фильтрации и получается обобщенная формула Дюпюи для дебита газа.
Из (13) можно получить время восстановления установившегося состояния в следующем виде:
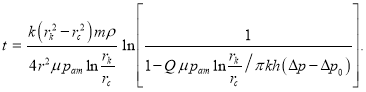(15)
Таким образом, в работе определяется время восстановления установившейся фильтрации газа в пористой среде, т. е. время перехода от неустановившегося состояния в установившееся.
Литература:
- Басниев К. С. Нефтегазовая гидромеханика /К. С. Басниев, Н. М. Дмитриев, Г. Д. Розенберг. — Москва-Ижевск: Институт компьютерных исследований, 2005.
- А.Х Мирзаджанзаде, Н.А Алиев, Х.Б Юсифзаде, Т.Ш Салаватов. Фрагменты разработки морских нефтегазовых месторождений. Элм-1997.
- И. Р. Гасанов. Определение времени релаксации при фильтрации неравновесной жидкости в пористой среде с учетом влиянии начального градиента. Международный научный журнал «Молодой учёный» № 51(289)- 2019 Декабрь, с. 234–235.
- Hasanov Ilyas Ravan, Jamalbekov Magomed Asaf, Hasanov Rauf Ilyas. Definition of the debit, speed of filtration and time of relaxation of the non-equilibrium liquid. Международный научный журнал «Молодой учёный» № 1(291) — 2020 Январь, с. 23–28.
