- Введение
Общая теория управления, теория систем оперирует с моделями, заданными в пространстве состояний. Построением таких моделей успешно занимались Р. Калман, Б.Л.Хо, Э. Зонтаг, Я. Виллемс, Р. Айсинг, ДЖ. Риссанен, П. Фурман и др. В случае точечных конечномерных реализаций эта проблема была решена Б.Л. Хо [1, с. 320].
Однако в реальной ситуации восприятие объекта управления не является точным в силу искажения информации, исходящей от объекта, "шумами" среды, через которую проходят информационные потоки. В связи с этим вектор состояния всегда содержит в себе некоторую ошибку в определении истинного состояния, которой соответствует некоторая объективная неопределенность.
Для разрешения сложившейся ситуации требуется привлечение специальных математических аппаратов, где диапазоны погрешностей исходных данных являются частью модели. В данной работе таким аппаратом служит интервальный анализ, так как параметры объекта являются интервалами.
Следует отметить, что свойства интервальной арифметики, как классической, так и полной являются неудовлетворительными. Например, даже в полной интервальной арифметике не выполняется дистрибутивность умножения относительно сложения, отсутствуют обратные элементы.
Из-за плохих свойств интервальной арифметики методы классической теории реализации оказываются неприменимыми. Несмотря на эту сложность в настоящее время сформулированы и обоснованы методы вычисления алгебраических реализаций для интервальных динамических систем: метод погружения в линейное пространство, метод граничных реализаций.
Охарактеризуем проблему реализации для интервальных динамических систем, метод граничных реализаций и докажем необходимое условие существования граничных реализаций для импульсной последовательности интервальных матриц.
2. Постановка задачи
В теории систем проблема реализации состоит в определении модели в пространстве состояний для динамической системы, заданной своим поведением вход-выход.
Задачу алгебраической реализации в [2, с. 78] определяют следующим образом: для заданной последовательности интервальных матриц размера 
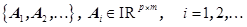(1)
определить математическую модель этой системы в пространстве состояний, т.е. размерность n и тройку интервальных матриц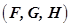 
таких, что выполняются интервальные уравнения
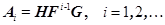, (2)
где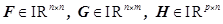 
, а матричные произведения выполняются справа налево, т.е. сначала вычисляется произведение 
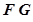, затем 
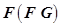и т.д.
Решить поставленную задачу не легко, т.к. в данном случае мы имеем дело с интервалами, а свойства интервальной арифметики являются неудовлетворительными. Тем не менее, Пушковым С.Г. и Калинкиной С.Ю. предложены методы решения этой задачи, в том числе метод граничных реализаций. Согласно этому методу проблема алгебраической реализации для класса интервальных систем, сводится к нахождению точечного решения. Метод граничных реализаций заключается в следующем: с импульсной последовательностью интервальных матриц, характеризующими поведение вход-выход динамической системы связывают две вещественные импульсные последовательности, определяемые верхними и нижними границами интервальных матриц.
Определение. Для последовательности интервальных матриц
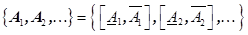(3)
реализации последовательности
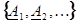
называют нижними граничными реализациями последовательности (1), а реализации последовательности
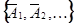
называют верхними граничными реализациями последовательности (1).
3. Методы решения
Теорема и следствие, сформулированные и доказанные в [2, с. 81] позволяют вычислять граничные реализации, в случае, когда матрицы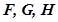 
удовлетворяют двум условиям: 1) полностью неотрицательны и 2) нижние границы 
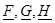не превосходят соответствующих им верхних 
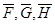. В том случае, когда найденные граничные реализации не удовлетворяют последнему условию, применяя преобразования подобия, находят соответствующую изоморфную реализацию, удовлетворяющую этому условию.
Однако зачастую при нахождении интервальных реализаций получается, что вычисленные граничные реализации и полученные изоморфные не удовлетворяет требуемым условиям и не позволяют сформировать искомую интервальную реализацию. Тогда, естественно, возникает вопрос, всегда ли существует искомая интервальная реализация? В данном вопросе помогает сориентироваться представленный в работе необходимый критерий существования реализуемости интервальных динамических систем.
4. Необходимый критерий реализуемости
Используя свойства матричных норм неотрицательных матриц [3, с. 358], можно доказать следующее предложение.
Предложение. Если для заданной импульсной последовательности интервальных матриц существует алгебраическая реализация, то для граничных реализаци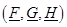й 
и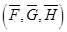 
найдется, по крайней мере, одна матричная норма
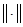, для которой имеет место оценка:
.
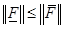Доказательство леммы опирается на теорему 5.6.7, а также теорему и следствие о граничных реализациях, представленных соответственно в [3, с. 358], [2, с. 81]. Приведем их формулировки с учетом используемых обозначений.
Теорема. Если 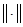— матричная норма на 
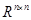и если матрица 
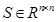невырождена, то формула 
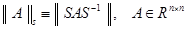, задает матричную норму.
Теорема о граничных реализациях. Если для нижней и верхней граничных реализаций одинаковой размерност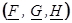и 
и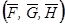 
некоторой последовательности интервальных матриц, выполняются условия:
1) 
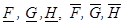— неотрицательные; (4)
2) 
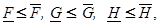(5)
то интервальная система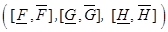 
является интервальной точной реализацией этой последовательности.
Следствие. Если для граничных реализаций одинаковой размерност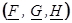и и 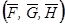некоторой последовательности интервальных матриц найдутся такие матрицы 
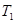и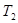 
,что выполняются неравенства
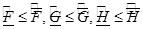
где
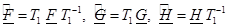, (6)
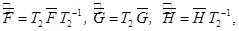(7)
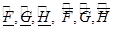— неотрицательные, то интервальная система 
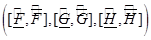является алгебраической интервальной реализацией этой последовательности.
Доказательство предложения.
Пусть для данной последовательности интервальных матриц существует алгебраическая реализация, тогда граничные реализаци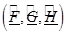и 
и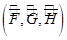 
удовлетворяют условиям теоремы и следствия, представленных в [2, с. 81], то есть
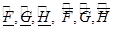— неотрицательные , (8)
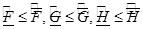, (9)
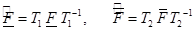, где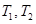 
невырожденные матрицы. (10)
Покажем, что хотя бы для одной матричной нормы выполняется неравенство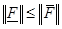 
.
Так как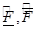 
удовлетворяют условиям (8), (9), то очевидно, что 
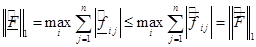, значит
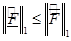. (11)
На основании теоремы 5.6.7. [3, с. 358] определим матричную норму 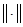при помощи формулы 
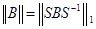, тогда имеем 
, 
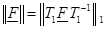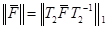. В силу условий (10) и (11) получаем требуемое неравенство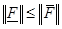. Предложение доказано.
Для иллюстрации данного критерия рассмотрим следующие примеры.
Пример 1. Рассмотрим полностью положительную интервальную импульсную последовательность для системы с одним входом и одним выходом:
.
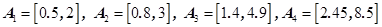Вычислим нижнюю и верхнюю граничные реализации последовательности с помощью алгоритма Б.Л. Хо.
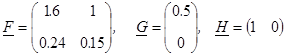, (12)
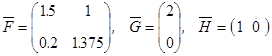. (13)
Вычисляя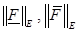 
, получим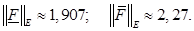 
Очевидно, что вычисленные матрицы (12), (13) не удовлетворяют требуемым условиям [2, с. 81]. Применим преобразования подобия для (12)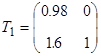 
, для (13) 
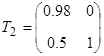получим
, 
.
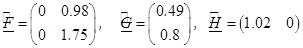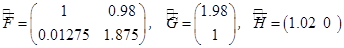Таким образом, искомая реализация исходной последовательности интервальных матриц имеет вид:
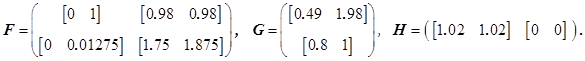
Пример 2. Рассмотрим полностью положительную интервальную импульсную последовательность для системы с одним входом и одним выходом:
.
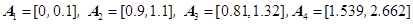Точечные реализации, нижняя и верхняя соответственно, имеют вид:
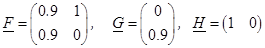, (14)
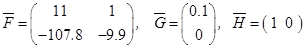. (15)
Определяя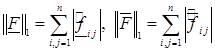 
, получим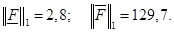 
Приведение реализаций (14) и (15) к наблюдаемой канонической форме позволяет получить искомую интервальную реализацию:
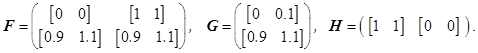
5. Заключение
Представленный в работе результат позволяет сориентироваться в вопросе существования граничных реализаций для импульсной последовательности интервальных матриц. Сформулированный и доказанный необходимый критерий реализуемости удобен и прост с вычислительной точки зрения.
Литература:
1. Калман Р., Фалб П., Арбиб М. Очерки по математической теории систем. - М.: Едиториал УРСС, 2004. – 400с.
2. Пушков С.Г., Кривошапко С.Ю. О проблеме реализации в пространстве состояний для интервальных динамических систем // Вычислительные технологии. – 2004, Т.9, №1. – С.75-85.
3. Хорн P., Джонсон Ч. Матричный анализ.- М.: Мир, 1989. – 656с.
