Численное определение предельно допустимой нагрузки на свод-арку из гофрированного U-образного тонкостенного профиля



Численное определение предельно допустимой нагрузки в своде-арке из гофрированного U-образного тонкостенного профиля при загружении равномерно распределенной нагрузкой.

Ключевые слова: напряжения в гофрированных и прямолинейных арочных элементах, быстровозводимые бескаркасные арочные здания, легкие конструкции, ангары.

Numerical determination of the maximum permissible load in the arch-arch of a corrugated U-shaped thin-walled profile when loaded with a uniformly distributed load.

Keywords: stresses in corrugated arch elements, stresses when working together straight and curved.

Сравнив напряжения и перемещения в арках из гофрированного U образного профиля, при гидростатическом и гравитационном давлении определили возникновение наибольших напряжений в прямолинейных элементах, не гофрированных, при закреплении из плоскости [1], [2]. Оценили напряженно деформированное состояние свода размерами dx на dy, и подтвердив экспериментальные данные численным методом по перемещениям получили расчетную схему для моделирования свода [3]. Определим предельно допустимую нагрузку на м2 по предельно допустимым перемещениям и нормальным напряжениям, в своде — арке закрепленного из плоскости в нижней полке, с одной стороны, как элемент свода [2], [3].

Материалы и методы: По твердотельной модели, выполненной в программном комплексе Solid Works в виде свода — арке полетом 18м и подъемом 8,5м из вальцованного профиля U образного сечения, загрузим радиальной и гравитационной нагрузками для определения распределения напряженно деформированного состояния свода и предельно допустимой нагрузки с закреплением из плоскости. Арочные профили были рассчитаны методом конечных элементов с незакрепленными верхними полками из плоскости, а нижней, что позволит максимально использовать поперечное сечение профиля и определить максимально допустимую нагрузку при различных формах загружений. Загружение приложено к гофрированной нижней полке.

Толщина профиля, мм	Напряжения (норм) МАХ,Н/м2	Напряжения (норм) МIN, Н/м2	Напряжения (танг) МАХ,Н/м2	Напряжения (танг) МIN, Н/м2	Величина нагрузки, Н/мм2	Перемещения в плоскости, мм	МАХ перемещ. стенок из плоскости, мм
0,6форма перем. рис.5«б»	2,00E+08	-3,57E+08	1,51E+08	-1,49E+08	0,0011044	гравит. 78,8	3,5
	1,92E+08	-3,43E+08	1,42E+08	-1,46E+08	0,0010551	гравит. 75,5	3,4
0,6форма перем. рис.5«а»	2,54E+08	-3,43E+08	3,93E+08	-8,16E+07	0,0013159	гравит. 83,0	7,2
1,0	1,43E+08	-3,57E+08	9,31E+07	-9,91E+07	0,0058478	радиа.7,8	4,6
	1,38E+08	-3,43E+08	8,95E+07	-9,53E+07	0,0056227	радиа.7,5	3,3
1,0форма перем. рис.5«б»	1,71E+08	-3,57E+08	9,31E+07	-1,50E+08	0,0020939	гравит. 70,16	1,90
	1,64E+08	-3,43E+08	8,94E+07	-1,44E+08	0,0020107	гравит. 67,17	1,87
1,0форма перем. рис.5«а»	2,40E+08	-3,57E+08	1,88E+08	-1,80E+08	0,0026797	гравит. 82,01	3,36
	2,26E+08	-3,43E+08	1,77E+08	-1,71E+08	0,0025535	гравит. 77,80	3,08
1,2форма перем. рис.5«б»	1.82E+08	-3.43E+08	1.12E+08	-1.53E+08	0.0028712	гравит. 77,6	3,2

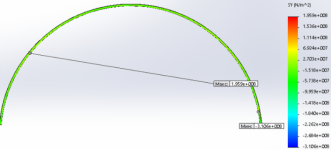
Рис. 1. Эпюра распределения нормальных напряжений вальцованного свода (при гравитационном давлении)

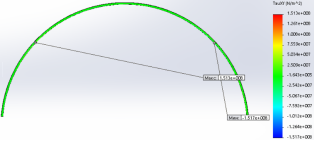
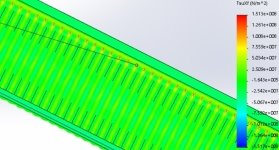
Рис. 2. Эпюра распределения тангенциальных напряжений вальцованного свода (при гравитационном давлении)

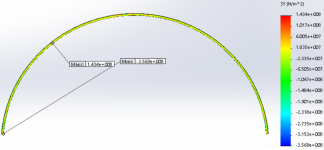
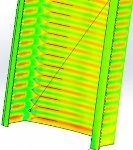
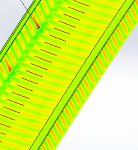
Рис. 3. Эпюра распределения нормальных напряжений в вальцованном профиле (при гидростатическом давлении)

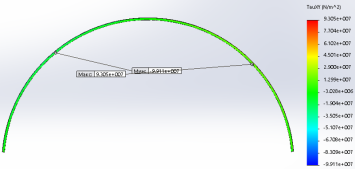
Рис. 4. Эпюра распределения тангенциальных напряжений в вальцованном профиле (при гидростатическом давлении)

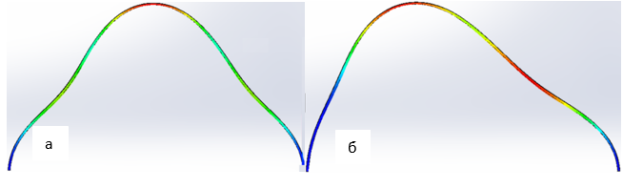
Рис. 5. Численные формы перемещений от равномерно распределенной нагрузки (при гравитационном давлении)

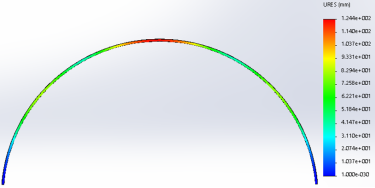
Рис. 6. Симметричная форма перемещений от не равномерно распределенной нагрузки (вертикальная нагрузка в левой верхней четверти отсутствует, тангенциальные напряжения близки к предельно допустимым)

Сравнивая, численно полученные распределения максимальных и минимальных нормальных напряжений с эпюрами усилий в 2 шарнирной арке получено не соответствие сечений по максимальным напряжениям, максимальные напряжения возникают в интервале, от узла закрепления или точки возникновения максимальных напряжений на 1–1,5 метра рис.1,2,4 при гравитационных нагрузках, при радиальных нагрузках интервалы меньше 0,5–1м. В расчете учитывается деформированное состояние конструкции.

Определенная предельная нагрузка отражена в таблице при условии перемещений по форме (а, б) рис. 5. (приблизительная величина предельно допустимой нагрузки по напряжениям (вычислена интерполяцией по одинаковым формам перемещений (а, б).

Результаты: численно определили предельно допустимые нагрузки приемлемые при соприкасающихся нижних полках профилей в своде и при загружении свода не по всей длине, так как незагруженные профили с противоположной стороны направления верхних полок, обеспечивают закрепление из плоскости, при небольших нагрузках. Показаны эпюры распределения напряжений на рис.1–4, на которых отражена работа нижней/верхних, гофрированных/прямолинейных участков при работе по данной расчетной схеме и отсутствие влияния несимметричного поперечного сечения(Мкр) рис.1,2. Распределение напряжения в нижней полке распределяются симметрично относительно оси поперечного сечения нижней полки [2]. При отсутствии закрепления из плоскости будет учитываться не симметричное сечение (Мкр). Тангенциальные напряжения относительно максимальной точки подъема имеют разные знаки рис.2 (М).

Обсуждения: на рис.6 показана симметричная форма перемещений от не равномерно распределенной вертикальной нагрузки.

Литература:

1. Карабутов М. С. Численное изменение напряжений и перемещений арки из гофрированного U-образного тонкостенного профиля при загружении критической нагрузкой // Молодой ученый. — 2019. — № 42. — С. 15–18. — URL
2. Карабутов М. С. Численное определение критической нагрузки по предельным перемещениям и напряжениям арки из гофрированного U-образного тонкостенного профиля при загружении гравитационной нагрузкой // Молодой ученый. — 2019. — № 43. — С. 19–22 — URL
3. Карабутов М. С. Сравнение численного анализа работы свода с эмпирическими данными и свода из гофрированного U-образного тонкостенного профиля // Молодой ученый.— 2020.—№ 4.—С.74–77.— URL.