Computer-mathematical modeling of the stress-strain state of two superficial kvershlags

In the last century, the works of foreign scientists was mainly theoretical research of stress-strain state of underground cavities in the isotropic massif. Using the symmetry of the biharmonic solutions and based on the special properties of harmonic functions O.Müller [1], K.Stocke [2] reviewed the relevant class of problems. G. V. Kolosov, N. I. Muskhelishvili [3] in the solution of plane problems of the theory of elasticity of an isotropic body has successfully used the methods of the complex variable theory.

Analytic function proposed by Appel, allowed to consider the state of the one-and many related isotropic body with a circular hole. L. A. Filshtinsky considered orthotropic structures with doubly periodic system of circular holes [4], and a body with elliptical holes A. S. Kosmodamiansky, M. M. Neskorodev [5]. A. S. Kosmodamiansky investigated the stress-strain state of an anisotropic elastic body with three and endless rows of holes, and based on these decisions Zh.S.Erzhanov, K. K. Kaydarov, M. T. Tusupov [6] studied the effects of the slots on the static stress state of underground workings. Zh.S.Erzhanov, Sh.M.Aytaliev and Zh.K.Masanov [7] proposed a computational mechanics and mathematical model of the anisotropic elastic deformation of the rock mass with doubly periodic systems slots and solve the problem by bringing the elastic constants obtained transtropic body, the equivalent stiffness main massif with slots, depending on the elastic properties and the geometry of the slits. On the basis of this model studied static initial elastic state mainly single underground cavities deep foundation of rigorous and approximate methods.

Significant contribution to the theory of finite element method and its application to solving complex problems of statics and dynamics of solid mechanics, scientists have L.Segerlind [8], B. Z. Amusin, A. B. Fadeev [9], Zh.S.Erzhanov T. D. Karimbaev [10], Sh.M.Aytaliev, Zh.K.Masanov, R. B. Baymahan, N. M. Mahmetova [11], N. T. Azhikhanov [12] and others.

In this case investigated the static elastic stress and strain state of two shallow cavities laying in heavy transtropic massif depending on the degree of discontinuity conform to small sloping layers at an angle . Let denote the depth of the workings of the distance between their centers .

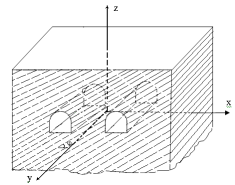
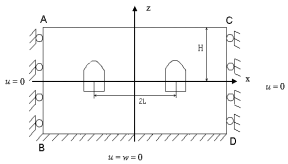
а) three dimensional view; b) two dimensional view;

Fig.1. The computational domain

Anisotropic doubly periodic massif of slits systems are replaced with solid transtropic body, equivalent stiffness basic structure, by solving the problem of reduction.

Hooke's law of anisotropic massif with cavities with generalized plane strain relative to the Cartesian coordinate system (see Figure 1) [7]:

; (1)

Here - effective elastic constants transtropic massif equivalent stiffness anisotropic massif with slits, which depends on the elastic constants of the last and the geometry of the slits .

The cross-section in plane ABCD shtrek planes of deformation using units to isoparametric calculation elements (Figure 1b). Constitute the basic resolution of the system of algebraic equations finite element method’s -order relative to the projections of moving points and it can be solved with the following boundary conditions [13]:

base BD calculation area ABCD non-deformable –

; (2)

sides АВ and СD under the weight of rocks moved only in the vertical direction due to a lack of influence of cavities –

. (3)

The study estimated the area with cavities is automatically split into isoparametric elements using program FEM_3D. Each point acts the vertical force of the weight (Figure 3).

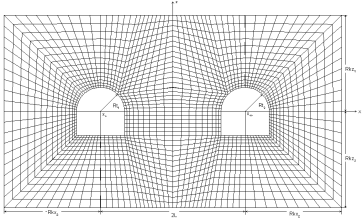
Fig.3. A layout of the estimated area for isoparametric elements

Solution of the fundamental system of equations with to finite element method’s displacement components with the boundary conditions (2), (3) strong methods is difficult; therefore it can be solved in an iterative method of Gauss-Seidel-relaxation factor with a given accuracy. An attractive feature of this method is as follows: firstly prepared only once and the system stiffness matrix used when iterating its elements and column elements of the matrix ; secondly, when - iteration for unknown , need values when - iteration, and for - their values for -iteration.

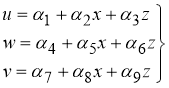(4)

Where factors is received from [13]. At this time, find function of the form as

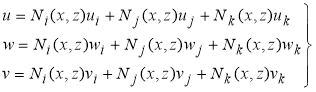(5)

Now shall determine connection between and . Where and Matrix stiffness of element

(6)

Thus, the system linear algebraic equation is formed [15]:

(7)

To verify the correct operation of the developed algorithms and software systems solved test problem of elastic stress state circular cavity in an anisotropic massif with the horizontal plane of isotropy in the plane strain and hydrostatic stress distribution in a intact massive. Unlike values of displacements at characteristic points of contour obtained by iterative and strict known methods, is no more than 1–2 %.

When calculating the components of displacements and stresses near boundaries shtreks of varying depth and the shape of the profile in slots transtropic massif with slits and inclined plane isotropy the study area was divided into 2064 elements with 2189 points.

For multivariate calculations defined an angle of inclination of the plane of isotropy (and the plane of the slits) slots massif with cavities, ceteris paribus both stress and displacement are distributed symmetrically around the vertical axis and increase with the depth of emplacement of structures; reduces stress, increasing displacement with reduction /a; when both the stress and the displacement are asymmetric about a vertical axis . When the length of the brattice 5D and more, where D-cavities of the largest diameter, interference structures is negligible.

1. Müller O. Untersuchungen an Karbongesteinen zur Klärung von Gebirgsdruckfragen. Glückauf, No. 47, pp. 1601–1612, 1930.
2. Stöcke K. Für das Gebingsdruckproblem wichtige Begriffe aus der technischen Mechanik. Zeitschrift für des Berg-Hütten und Salinenwesen. Bd. 84, H. 11, pp. 465–467, 1937.
3. Muskhelishvili N. I. Some basic problems of the mathematical theory of elasticity. M.: Science, 707p. 1966.
4. Filshtinsky L. A. Stress in the correct doubly periodic grids (lattices). «Engineering magazine. Mechanics of Solids ", No. 1, pp. 20–28, 1967.
5. Kosmodamianski A. S., Neskorodev M. M. Doubly periodic problem for an anisotropic structure weakened elliptical holes. «Reports of the Academy of Sciences URSR Ser. A ", No. 7, pp.31–42, 1970.
6. Erzhanov Zh.S, Kaidarov K. K., Tusupov M. T. Mountain range with a discontinuous layer coupling (plane problem). «Mechanical processes in the rock mass”. Alma-Ata, «Nauka”, 189p, 1969.
7. Erzhanov Zh.S, Aytaliev Sh.M., Masanov Zh.K. Stability of horizontal caves in the pan-layered massif. Alma-Ata, Science, 160p, 1971.
8. Segerlind L. Application of the finite element method. — Moscow: Mir,392p, 1979.
9. Amusin B. Z., Fadeev A. V. The finite element method for solving mining mechanics. Moscow: Nedra, 142p, 1975.
10. Erzhanov Zh.S., Karimbayev T. D. The finite element method in problems of rock mechanics. Alma-Ata: Science, 238p, 1975.
11. Aytaliev Sh.M., Massanov Zh.K, Baimakhanov I. B., Makhmetova N. M. FEM: Seismic stress state paired tunnels. Numerical methods for solving problems of solid mechanics. Karaganda, pp. 3–15, 1987.
12. Azhikhanov N. T. Computer simulation of oil extraction problems in heterogeneous environments. With curved boundaries. LAP Lambert Academic Publishing — ISBN: 978–3-8443–2856–1. 142p, 2012.
13. B. T. Zhumagulov, Zh.K.Masanov, N. T. Azhikhanov, T. A. Turumbetov. Mathematical modeling and stressed state of the coupled tonnels in the anisotropic environment. //BOOK OF ABSTRACTS IV congress of the Turkic world mathematical society. Baku, Azerbaijan. p.505. 1–3 July, 2011.
14. Shabrov N. The finite element method in calculations of details of thermal engines. –Leningrad, Mashinostroenie, 212 p, 1983.
15. T.Turymbetov, N.Azhikhanov, N.Zhunisov, Zh.Aimeshov Stress-strain state of two diagonal cavities weighty inclining layered massif system with slots in terms of elastic-creep deformations. World conference on technology, innovation and entrepreneurship, Procedia-Social and Behavioral Sciences (ISSN: 1877–0428), 195, Istanbul, Turkey, 2015. pp. 2263–2271.