В данной статье рассматриваются способы устранения неопределенностей при разработке экспертной системы, что является главным преимуществом системы.
Ключевые слова: нейронные сети, обучение, подготовка начальных значений весовых коэффициентов, планирование выходных значений.
Человек-эксперт в своей области годами копит свой опыт, опираясь на теоретические знания и примеры прошлых лет. Некоторые действия теперь для него, как привычка. Пропуская промежуточные действия, человек-эксперт может прийти к выводу.
Основное преимущество экспертных систем — способность справиться с неопределённостью также, как это делает человек-эксперт в данной области. Для этого необходима база, созданная человеком-экспертом в данной области. В нее включаются все прошлые опыты как удачные, так и неудачные. В основе рассуждений неопределенностей лежит теория вероятности.
Главное утверждение Заде [Zadeh, 1983] заключается в том, что теория вероятности является хорошим инструментом для измерения случайности информации, но не подходит для измерения смысла информации. [2, с. 344]
Любой человек сталкивается с неопределённостью в своей жизни. Например, человек учит правила дорожного движения, проходит практику вождения и в итоге получает становиться экспертом в этой области и получает права. Люди понимают, как эффективнее запоминать слова при изучении нового языка. Понимают, как справиться с холодом, когда на улице холод, а автобус никак не едет на остановку.
Неопределенность — нехватка адекватной информации. [1, c. 296]
1. Байесовская вероятность.
Теория Байеса способна рассчитать вероятность на основе случайных событий. В формуле 1 используется определения априорной вероятности и апостериорной. Априорная вероятность ![]() — вероятность, которая присвоена данному событию без каких-либо других знаний. Апостериорная
— вероятность, которая присвоена данному событию без каких-либо других знаний. Апостериорная ![]() — вероятность, при условии, что произошло событие.
— вероятность, при условии, что произошло событие.
При этом можно если данные события независимы, то результатом будет произведение этих событий.
2. Байесовские сети доверия.
При применения предыдущего способа могут возникнуть трудности, которые могут быть неприменимы для использования в реальной жизни.
В данном методе предлагается модель рассуждения с наилучшими объяснениями множества данных в контексте ожидаемых первичных связей в предметной области.
Основная суть в том, что человек-эксперт выбирает явления, которые изначально связаны друг с другом и выражает вероятности или меры влияния лишь для этих события. Считая при этом, что остальные события не влияют. На данные или же, что их влияние настолько мало, что ими можно пренебречь.
3. Теория Демпстера-Шафера.
Метод рассматривает множества предположений и ставит в соответствие каждому из них вероятностный интервал доверия, которому должна принадлежать степень уверенности в каждом предположении.
Мера правдоподобия ![]() представлена уравнением 2, где
представлена уравнением 2, где
– ![]() — мера доверия;
— мера доверия;
– ![]() — мера доверия предположению;
— мера доверия предположению;
При этом, если ![]() обосновано, то есть
обосновано, то есть ![]() , следовательно,
, следовательно, ![]() .
.
Теорема Демстера-Шафера была предложена им в 1968 году и заключалась в основных двух идеях. Первая — получение степени доверия для данной задачи из субъективных свидетельств о связанных с ней проблемах, вторая — использование правила объедения свидетельств, если они независимы. [2, c. 352]
4. Теория нечетких множеств.
Пусть S — множество, а s — элемент множества. Нечеткое подмножество F множества S определяется функцией принадлежности mF(s), задающей «степень» принадлежности s к F. [2, с. 345].
Каждое число может принадлежать множеству с какой-то долей достоверности. Например, на рис. 1 представлена функция принадлежности роста человека к понятиям “низкий рост”, “средний рост”, “высокий рост”.
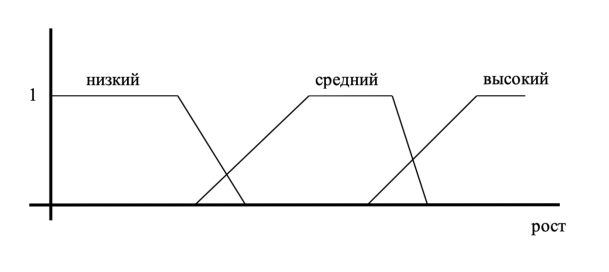
Рис. 1. Нечеткие множества, представляющие низких, средних и высоких людей
Вывод
Устранение неопределенности — это основное преимущество экспертной над обычными алгоритмами. Каждый метод, приведенный в этой статье, имеет преимущества и недостатки. Поэтому разработчику нужно будет исходя из своего задания, выбрать нужный метод.
Литература:
1. Люгер, Джоррдж Ф., Искусственный интеллект: стратегии и методы решения сложных проблем. — М.: Вильямс, 2003.
2. Ждарратано Д. Экспертные системы. Принципы разработки и программирование. — М.: Вильямс, 2007.







