В статье авторы пытаются получить математические зависимости угла поворота продольной оси монорельсового транспортного средства во времени, угловые скорость и ускорение в зависимости от скорости движения, радиуса кривизны монорельса и базы транспортного средства.
Ключевые слова: монорельсовое транспортное средство, параметры движения на повороте.
Для определения нагрузок, действующих на монорельсовое транспортное средство и на груз, размещенный в нем, при переходе с прямолинейного на криволинейный участок пути, необходимо знать такие параметры движения, как изменение угла поворота продольной оси ТС во времени, угловые скорость и ускорение. Указанные параметры движения зависят не только от скорости и времени, но и от расстояния между опорами (базы) ТС, а также радиуса кривизны монорельса. Поэтому необходимо иметь зависимости:
![]() ,
, ![]() ,
, ![]() ,
,
где ![]() ,
, ![]() ,
, ![]() — соответственно угол поворота, угловые скорость и ускорение соответственно, V- скорость движения, t — время, с — база ТС, R — радиус закругления монорельса.
— соответственно угол поворота, угловые скорость и ускорение соответственно, V- скорость движения, t — время, с — база ТС, R — радиус закругления монорельса.
Будем рассматривать движение ТС при переходе с прямолинейного участка пути на криволинейный и определять значение угла поворота продольной оси ТС с момента прихода передней опоры к точке сопряжения В до момента прихода в эту точку задней опоры (рис. 1). Итак при t=0 ТС занимает положение ![]() . Передняя опора находится в точке В, задняя в точке
. Передняя опора находится в точке В, задняя в точке![]() . Рассмотрим положение транспортного средства в произвольный момент времени до прихода задней опоры в точку В. Пусть в момент времени t задняя опора находилась в точке А, а передняя — в точке D на криволинейном участке пути. Радиус закругления монорельса обозначим через R0. Транспортное средство движется с постоянной скоростью V.
. Рассмотрим положение транспортного средства в произвольный момент времени до прихода задней опоры в точку В. Пусть в момент времени t задняя опора находилась в точке А, а передняя — в точке D на криволинейном участке пути. Радиус закругления монорельса обозначим через R0. Транспортное средство движется с постоянной скоростью V.
Обозначим угол DAF через ![]() и определим зависимость угла
и определим зависимость угла ![]() от времени t, скорости движения транспортного средства V, его базы с и радиуса R0. Итак,
от времени t, скорости движения транспортного средства V, его базы с и радиуса R0. Итак, ![]() . (1)
. (1)
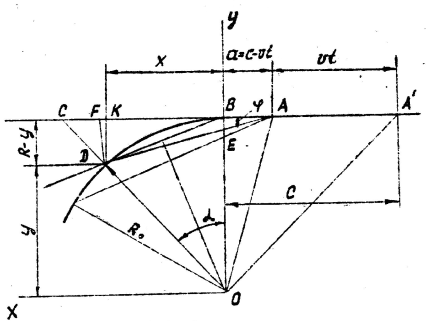
Рис. 1. Схема движения
Рассмотрим рис.1, на котором ![]() ;
; ![]() ;
; ![]() ;
;
Из вершины D опустим перпендикуляр DK на сторону AF треугольника DAF и определим отрезок DK.
![]() . (2)
. (2)
Из треугольника ОВС определим ОС
![]() .
.
Сторона DC треугольника DKC составляет часть отрезка ОС
![]() . (3)
. (3)
Из треугольника DKC определим сторону DK
![]() =2
=2![]() , (4)
, (4)
так как угол α равен углу СОВ и равен углу CDK, как соответственные углы при параллельных прямых ОВ и DK.
Используя зависимости (2) и (4), получим равенство
откуда ![]() =
=![]() . (6)
. (6)
Определим сторону ВК из треугольника DBK
![]() (7)
(7)
При этом ![]() по построению. FK определим из прямоугольного треугольника DKF
по построению. FK определим из прямоугольного треугольника DKF
![]() , откуда
, откуда
![]() . (8)
. (8)
Найдем квадрат гипотенузы DB из треугольника DBK
![]() . (9)
. (9)
В треугольнике DOB опустим перпендикуляр из вершины О на сторону DB. Так как треугольник DOB равнобедренный, то ВО = DО, тогда
![]() и
и ![]() . (10)
. (10)
Возведем выражение (10) в квадрат и приравняем правые части полученного выражения и выражения (9), тогда получим
![]() (11)
(11)
Используя зависимость (6), преобразуем выражение (11). После подстановки (6) в (11) и несложных преобразований получим следующее уравнение
![]() . (12)
. (12)
Воспользуясь следующими равенствами:
![]() ,
, ![]() и
и ![]() , преобразуем выражение (12) и получим новое уравнение
, преобразуем выражение (12) и получим новое уравнение
![]() . (13)
. (13)
Вынеся за скобки (1+![]() и приравняв оставшуюся часть к нулю, получим
и приравняв оставшуюся часть к нулю, получим
![]() . (14)
. (14)
Выразив ![]() и проведя несложные алгебраические преобразования, получим следующее квадратное уравнение
и проведя несложные алгебраические преобразования, получим следующее квадратное уравнение
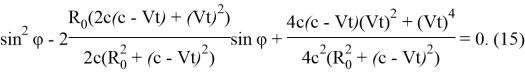
Решая данное уравнение, получим
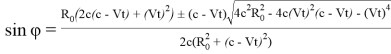 . (16)
. (16)
Откуда
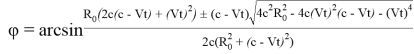 . (17)
. (17)
Найдем выражение для максимального значения угла ![]() .
.
![]() . (18)
. (18)
Воспользовавшись зависимостью (6), определим ![]()
![]() . (19)
. (19)
Максимальное значение угла ![]() наступает в том случае, когда задняя опора транспортного средства займет положение в точке В, тогда стороны AD и BD совпадут, то есть BD=c. В соответствии с рис. 1 в этом случае
наступает в том случае, когда задняя опора транспортного средства займет положение в точке В, тогда стороны AD и BD совпадут, то есть BD=c. В соответствии с рис. 1 в этом случае
![]() . (20)
. (20)
Подставив выражение (20) в зависимость (19) и сократив обе части на ![]() , получим
, получим ![]() или
или ![]() , (21)
, (21)
где α зависит от базы транспортного средства с и радиуса закругления монорельса
Результаты анализа зависимости (17) и результаты расчетов по формулам (17), (20), (21) показали, что в формуле (17) необходимо перед корнем брать знак минус, поэтому
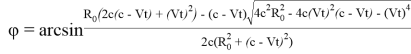 . (22)
. (22)
Можно предложить другой подход для получения уравнения (15). При переходе от прямолинейного участка пути к криволинейному транспортное средство переходит от поступательного движения к плоскому. Условия для получения уравнения аналогичны описанным выше.
Выберем начало координат XOY в точке О, совпадающей с центром кривизны криволинейного участка. Тогда
![]() . (23)
. (23)
Уравнение окружности монорельса на повороте имеет вид
![]() . (24)
. (24)
Определим координату У для точки D
![]() . (25)
. (25)
Учитывая, что ![]() , находим
, находим
Величина «а» в соответствии с условиями задачи и геометрическими построениями (Рис.1) определяется зависимостью
![]() . (27)
. (27)
Подставим формулу (27) в выражение (26) и получим
![]() . (28)
. (28)
Для исключения координаты «У» воспользуемся зависимостью
![]() , тогда
, тогда
![]() . (29)
. (29)
Выполним последовательно ряд формальных преобразований с целью избавления от корня и получения зависимости функции ![]() от параметров монорельса и транспортного средства, для чего возведем в квадрат левую и правую части равенства (29)
от параметров монорельса и транспортного средства, для чего возведем в квадрат левую и правую части равенства (29)
![]()
Проведя несложные преобразования с этим равенством, получим следующее уравнение
Поделим обе части последнего уравнения на коэффициент при ![]() и, выполнив элементарные преобразования, получим
и, выполнив элементарные преобразования, получим
![]() . (31)
. (31)
В уравнении (31) выразим ![]() следующим образом
следующим образом ![]() .
.
После чего возведем в квадрат левую и правую части уравнения. Проведя преобразования получим
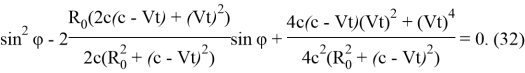
Таким образом, полученное уравнение (32) полностью совпадает с выражением (15). Решения уравнений (32) и (15) вида (22) дают весьма громоздкие выражения для угловой скорости ![]() и углового ускорения
и углового ускорения ![]() Поэтому вернемся к уравнению (30) и получим решение в несколько другом виде. Введем новые величины
Поэтому вернемся к уравнению (30) и получим решение в несколько другом виде. Введем новые величины
![]() ;
; ![]() ;
; ![]() .
.
Очевидно, что ![]() , откуда
, откуда
![]() . (33)
. (33)
С учетом преобразований ![]() или
или
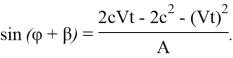
Так как ![]() ,
,
![]() , то
, то
![]() , или
, или
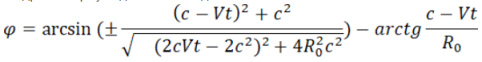 (34)
(34)
Можно показать, что решение (34) уравнения (30) приводится к виду (17). Однако, как уже отмечалось, получение первой и второй производных от ![]() значительно проще при использовании выражения (34).
значительно проще при использовании выражения (34).
Расчеты с использованием зависимостей (20), (21), (34) показали, что знак под функцией ![]() должен быть «плюс».
должен быть «плюс».
Угловая скорость движения транспортного средства при переходе на криволинейный участок монорельса получается в результате дифференцирования зависимости (34)
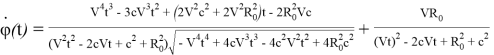 (35)
(35)
Угловое ускорение движения транспортного средства при переходе на криволинейный участок монорельса получается в результате дифференцирования зависимости (35). На рис. 2…4 показаны графики зависимостей ![]() ,
, ![]() .
.
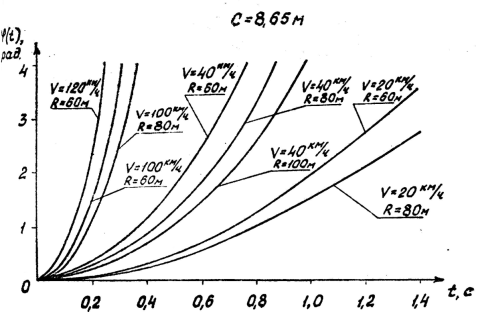
Рис. 2. Зависимость угла поворота продольной оси ТС от времени при различных значениях скорости, радиусах закругления монорельса и фиксированной базе
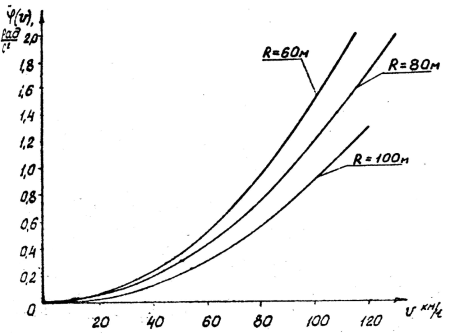
Рис. 3. Зависимость углового ускорения продольной оси ТС от скорости при различных радиусах закругления монорельса и фиксированной базе
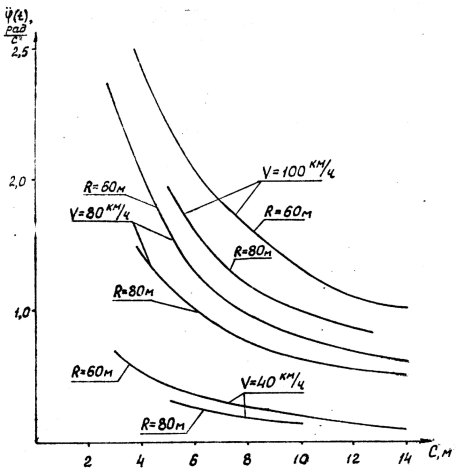
Рис. 4. Зависимость углового ускорения продольной оси ТС от базы при различных радиусах закругления монорельса и скоростях движения
Полученные в статье математические зависимости могут быть использованы для определения нагрузок, действующих на монорельсовое транспортное средство и на груз, размещенный в нем, при переходе с прямолинейного на криволинейный участок пути.
Литература:
- Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов.- 13-е изд., исправленное.- М.: Наука, Гл. ред. физ.-мат. лит., 1986. — 544 с.







