В данной работе подробно рассмотрена задача маршрутизации транспорта с временными окнами и ограниченной грузоподъёмностью. В ходе работы рассматриваются различные эвристические и мета-эвристические алгоритмы, применённые к данному типу задач. Более подробно были изучены и реализованы на языке программирования Python 3.8 алгоритмы имитации отжига, поиска по запретам и управляемый локальный поиск. Был произведён анализ эффективности алгоритмов на сетях больших размерностей.
Ключевые слова: CVRPTW, мета-эвристика, имитация отжига, поиск по запретам, локальный управляемый поиск.
Проблема маршрутизации транспорта (Vehicle Routing Problem –VRP) впервые была сформулирована в статье [1], как обобщенный случай задачи коммивояжера, где была поставлена математическая формулировка, и решена задача о поставке бензина на заправочные станции. На сегодняшний день эта задача является одной из значимых и актуальных задач в области современной комбинаторной оптимизации.
Классическая задача маршрутизации транспорта выглядит следующим образом: k транспортных средств, первоначально находящихся в депо, должны доставить товары m потребителям. Цель задачи — это минимизация затрат на перевозку товара. Решением VRP задачи является нахождение множества маршрутов, где: маршрут начинается и заканчивается в депо; каждый клиент может быть посещён только один раз.
Затраты на перевозку могут быть уменьшены [2] с помощью оптимизации пройденного расстояния, а также использования меньшего количества транспорта.
В данной работе исследуется задача, в которой вводится ограничение на то, что транспортное средство имеет конкретную вместительность и каждый клиент может быть обслужен только в индивидуальное временное окно (Capacitated VRP with Time Windows — CVRPTW).
Авторы [3] вводят понятия временных окон: «мягкие» и «жёсткие». Их основное отличие заключается в том, что если водитель опаздывает к потребителю с «мягкими» временными окнами, то продукция будет принята, но будет налагаться штраф. В ситуации с «жесткими» временными окнами, в случае опоздания, продукция будет не принята в полном размере. Так же авторы доказывают, что решение будет оптимальным, если товар будет доставлен не позже заданной правой границы «жёсткого» временного окна.
В работе я сосредоточу своё внимание на «жёстких» временных окнах, где исследования процветают в течение многих десятилетий. Такие ограничения чаще применяются на практике, начиная от деятельности доставки еды и скорой помощи, до маршрутизации общественного транспорта [4].
Математическая постановка
Задача транспортной маршрутизации может быть определена как ориентированный граф G = (N, E) с множеством узлов N = D ![]() {0, n+1}, где D = {1,…,n} — множество потребителей, 0 — это «стартовое» депо, n+1 — это «возвратное» депо. Пусть E = { (i, j): i, j
{0, n+1}, где D = {1,…,n} — множество потребителей, 0 — это «стартовое» депо, n+1 — это «возвратное» депо. Пусть E = { (i, j): i, j ![]() D}
D} ![]() { (0, i): i
{ (0, i): i![]() D}
D} ![]() {(n+1, i): i
{(n+1, i): i ![]() D} — дуги сети. R = {r1,…,rn} — множество запросов, при котором каждый запрос r
D} — дуги сети. R = {r1,…,rn} — множество запросов, при котором каждый запрос r ![]() D. С каждой дугой (i, j)
D. С каждой дугой (i, j) ![]() E, где i
E, где i![]() j, мы связываем время транспортировки tij, которое в себя может включать время обслуживания у клиента, и стоимость транспортировки cij.
j, мы связываем время транспортировки tij, которое в себя может включать время обслуживания у клиента, и стоимость транспортировки cij.
Также пусть V будет множеством одинаковых транспортных средств с ограниченной вместительностью (грузоподъёмностью) Q транспорта для груза.
Каждый узел связан с временными окнами [ai, bi], где ai и bi представляют собой минимальное и максимальное время прибытия к i-ому потребителю.
Задачей CPRVTW является нахождение множества S маршрутов для транспортных средств VS ![]() V с целью минимизации затрат на перевозку с учётом спроса в узлах, временных окон и вместительность транспорта.
V с целью минимизации затрат на перевозку с учётом спроса в узлах, временных окон и вместительность транспорта.
В задаче CVRPTW мы рассмотрим целевую функцию:
- Минимизировать количество используемых транспортных средств, что является доминирующим фактором при расчете затрат на транспортировку.
- Минимизировать общую длину транспортного плана.
Чтобы сформулировать CVRPTW в виде задачи линейного программирования, необходимо рассмотреть следующую систему уравнений, которая содержит два набора переменных x иs. Для каждой дуги (i, j), где i![]() j, i
j, i![]() n+1, j
n+1, j![]() 0, и каждое транспортное средство мы определяем
0, и каждое транспортное средство мы определяем ![]() как
как
![]()

![]() Решающая переменная
Решающая переменная ![]() определяется для каждой вершины i и каждого транспортного средства k и обозначает время, когда транспортное средство k начинает обслуживать клиента i. В случае, если транспортное средство k не обслуживает клиента i,
определяется для каждой вершины i и каждого транспортного средства k и обозначает время, когда транспортное средство k начинает обслуживать клиента i. В случае, если транспортное средство k не обслуживает клиента i, ![]() не имеет значения, и, следовательно, его стоимость считается неактуальной. Мы предполагаем, что a0 = 0 и, следовательно,
не имеет значения, и, следовательно, его стоимость считается неактуальной. Мы предполагаем, что a0 = 0 и, следовательно, ![]() = 0 для всех k.
= 0 для всех k.
 (1)
(1)
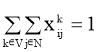
![]() (2)
(2)
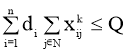
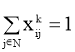
![]() (4)
(4)
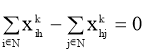
![]() (5)
(5)
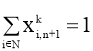
![]() (6)
(6)
![]()
![]() (7)
(7)
![]()
![]() (8)
(8)
![]()
![]() (9)
(9)
Целевая функция (1) минимизирует общую стоимость поездки. Ограничение (2) показывает, что каждый клиент посещается только один раз, и (3) утверждает, что транспортное средство может быть загружено до его предела вместительности. Уравнения (4), (5), (6) указывают на то, что каждое транспортное средство должно покинуть депо 0; после того, как транспортное средство прибывает к клиенту, оно должно уехать в другой пункт назначения; и наконец, все транспортные средства должны прибыть в депо n+1. Неравенство (7) устанавливает взаимосвязь между временем отправления транспортного средства от клиента до его непосредственного приемника. Наконец, ограничение (8) подтверждает, что временные окна соблюдаются, а (9) являются ограничениями целостности.
Мета-эвристические алгоритмы решения задачи
Точные алгоритмы характерны тем, что дают оптимальное решение, но их минус заключается в том, что они имеют большую зависимость от размерности задачи.
Эвристические алгоритмы характерны тем, что основаны на некотором правиле (эвристике), правильность которого для всех возможных случаев не доказана, но в подавляющем числе большинства случаев дают решение близкое к оптимальному.
Мета-эвристические алгоритмы характерны тем, что являются объединением основных эвристических методов в рамках алгоритмических схем более высокого уровня. Преимуществом мета-эвристических перед эвристическими алгоритмами является то, что они могут избегать попадание в локальные экстремумы, тем самым алгоритм позволяет работать с задачами больших размерностей, при этом решая их точнее, и без сильных временных затрат.
В данной работе были использованы и реализованы на языке Python 3.8 алгоритмы имитации отжига (simulated annealing) [5], поиска по запретам (tabu search) [6] и управляемый локальный поиск [7] (guided local search) c использование чередующегося спуска поиска окрестностей (Variable Neighborhood Descent — VND) [8].
Поиск окрестностей в себя включает алгоритмы локального поиска: стохастический, 2-opt и перекрёстный обмен.
Применение алгоритмов
Для проведения эксперимента были рассмотрены 2 различные базы данных, две из которых, Solomon на 100 узлов и Homberger на 1000 узлов, находятся в свободном доступе на сайте http://neo.lcc.uma.es/vrp/vrp-instances/.
В качестве критерия остановки алгоритмов мета-эвристики является время, равное 300 секунд, а также любого из алгоритмов локального поиска, равное 5 секунд. Начальное решение было получено с помощью жадного алгоритма.
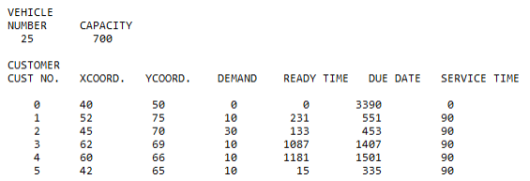
Рис. 1. Фрагмент из файла тестовой задачи
Выводы
На сетях большого размера, получение минимума целевой функции, из-за вычислительной сложности задачи приводит не к идеальным, но допустимым результатам.
Проведённые исследования показали, что алгоритмы мета-эвристики способны получать достаточно близкие к оптимальным результатам значения.
В таблице 1, мы можем наблюдать % решений, которые удовлетворяют допущению близости отклонения в 15 % от оптимального решения в пользу меньшего количества времени вычисления.
Таблица 1
Статистика допущения
|
База данных |
Размерность |
SA |
TS |
GLS |
|
Solomon |
100 |
0.84 |
0.93 |
0.93 |
|
Homberger |
1000 |
0.25 |
0.25 |
0.3 |
Исходя из результатов таблицы, мы можем сделать вывод, что принцип алгоритма мета-эвристики управляемого локально поиска (GLS) в большем количестве случаев даёт лучшие результаты.
Заключение
В данной работе были рассмотрены различные задачи маршрутизации транспорта и подробно исследован один из этих видов — задача маршрутизации транспорта с временными окнами и ограниченной грузоподъёмностью. Были изучены различные мета-эвристические подходы к решению данного типа задач: имитация отжига (SA); поиск с запретами (TS); управляемый локальный поиск (GLS). Данные алгоритмы были реализованы на языке Python 3.8 и рассмотрены на тестовых данных.
Оценка результатов эксперимента выявила наилучший алгоритм.
Литература:
- Dantzig, G.B., Ramser J. H. — «The Truck Dispatching Problem», 1959.
- P. Toth, D.Vigo. — «An Overview of Vehicle Routing Problems». The Vehicle Routing problem, SIAM, pp. 1–26, 2002.
- Cordeau, J.-F., Desaulniers, G., Desrosiers, J., and Soumis, F. — «The VRP with time windows». In: The vehicle routing problem, pp. 157–193, SIAM Monographs on Discrete Mathematics and its Applications, 2002
- Hempsch C., Irnich S. — «Vehicle Routing Problems with Inter-Tour Resource Constraints», 2008.
- O. Arbelaitz, C. Rodriguez and I. Zamakola. — «Low Cost Parallel Solutions for the VRPTW Optimization Problem», International Conference on Parallel Processing Workshops. IEEE Computer Society. Valencia, Spain. pp. 176–181, 2001.
- J.-F. Cordeau, G. Laporte, A. Mercier. — «A unified tabu search heuristic for vehicle routing problems with time windows». Journal of the Operational Research Society 52, 928–936. 2001.
- Kilby, Philip & Prosser, Patrick & Shaw, Paul. — «Guided Local Search for the Vehicle Routing Problem». 10.1007/978–1–4615–5775–3_32, 2002.
- Marwa Harzi,Saoussen Krichen — «Variable neighborhood descent for solving the vehicle routing problem with time windows». Electronic Notes in Discrete Mathematics, pp. 175–182, 2017.







