Бұл мақалада біз геометриялық мазмұнды сызықты дифференциалдық теңдеулерді құру және оның шешу жолдарын ұсынамыз.
Дифференциалдық теңдеулерді құруға келесі есептер білім алушылардың математикалық модельдеуге дағдылануына жалпы математикалық білімді тереңірек игеруіне үлкен ықпал етеді.
Енді бірнеше нақты мысалдарды шешу әдістерімен толық сызбасымен бірге қарастырайық.
1-мысал. A (а;a) нүктесі арқылы өтетін және кез-келген M (x; y) нүктесінде PM ординаты бар қисыққа жүргізілген жанама Oy осімен T нүктесінде қиылысқанда жүргізілген жанама Oy осімен T нүктесінде қиылысқанда, шыққан OTMP трапециясының ауданы а2-қа тең болатындай қисықтың теңдеуін жазыңдар (сурет 1).
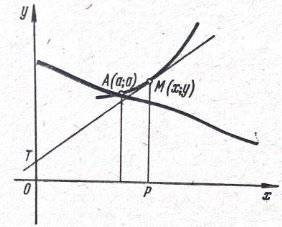
Сурет 1.
Шешуі. Трапецияның ауданы S=![]() формуласымен табылады. OT=y-xy’, PM=y, а OP=x болғандықтан, мынадай дифференциалдық теңдеуді құрамыз:
формуласымен табылады. OT=y-xy’, PM=y, а OP=x болғандықтан, мынадай дифференциалдық теңдеуді құрамыз:
![]()
немесе
![]() . (1)
. (1)
Бұл сызықтық теңдеу. Сызықтық теңдеудегі жалпы шешімін табу ережесіне сәйкес
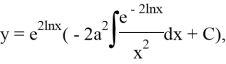
![]() немесе
немесе ![]() болса,
болса,
Соған сәйкес
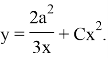
Бастапқы шартты x=a, y=a жалпы шешімге қою арқылы, C=1/(3a) екенін табамыз, ізделінді қисықтың теңдеуі мынадай болады:
![]() (2)
(2)
2-мысал. А (2; -2) нүктесі арқылы өтетін және кез-келген M (x;y) нүктесі арқылы өтетін қисықтың теңдеуін табыңдар, егер ОМ радиус-вектор мен MP жанамасын Ox осімен қиылысуынан шыққан үшбұрыштың ауданы 2-ге тең болса(2-сурет).
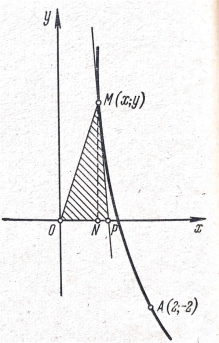
Сурет 2.
Шешуі. Үшбұрыштың ауданы ![]() формуласымен анықталады, MN = y болғанда M нүктесінің ординатасы, ал OP = x-
формуласымен анықталады, MN = y болғанда M нүктесінің ординатасы, ал OP = x- ![]() . Дифференциалдық теңдеу мынадай түрде беріледі:
. Дифференциалдық теңдеу мынадай түрде беріледі:
немесе
![]() (3)
(3)
Бұл белгісіз у аргументінің х функциясына қатысты сызықтық дифференциалдық теңдеу.
Жалпы интегралды жоғарыдағыдай табамыз:
![]() немесе
немесе ![]()
х=2 болғанда у=-2, сондықтан, С=-3/2, келесідей ізделінді қисықтың теңдеуін аламыз:
3у2+2ху-4=0.
3-мысал. Кез-келген нүктесінен жүргізілген нормалымен осіне дейінгі қашықтыққа сәйкес кесіндінің ортасы у2=ах параболасында жататын және координатаның бас нүктесінен өтетін қисықтың теңдеуін табыңдар.
Шешуі.
Қисықтан кез-келген нүктесін М(х;у)-ден белгілейміз. Р нүктесінің М нормаль нүктесімен қиылысуы Ох осінде келесідей координаттарға ие: х+уу’ және 0, MP нормасы кесіндісінің ортасы N нүктесінің координаттары xN=x+![]() және
және ![]() болады. N нүктесі y2=ax параболасында жатқандықтан, оның координаттары параболаның теңдеуін қанағаттандырады. Яғни,
болады. N нүктесі y2=ax параболасында жатқандықтан, оның координаттары параболаның теңдеуін қанағаттандырады. Яғни,
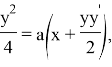
немесе
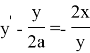
болады.
Дифференциалдық теңдеу құрылды және бұл (n= -1) Бернулли теңдеуі. Оны келесідей түрлендіреміз 2yy’-![]() және
және ![]() соған сәйкес 2yy’=z’ болады.
соған сәйкес 2yy’=z’ болады.
Теңдеу сызықтық түрге келтіріледі:
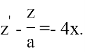
Жалпы шешім
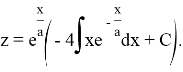
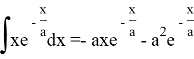
болғандықтан,
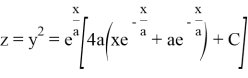
болады немесе
![]() +4
+4![]()
Бастапқы шарты у=0 х=0 болғанда С=-4а2 болатыны белгілі. Ізделінде қисықтың теңдеуі келесідей:
![]() +4
+4![]()
Әдебиет:
- Самойленко А. М., Крирошея С. А., Перестюк Н. А. Дифференциальные уравнения: примеры и задачи. — М., 1989.
- Әбілқасымова А., Жұмағұлова З. Алгебра және анализ бастамалары: 11 сынып. — Алматы: Мектеп, 2015.







