В данной статье описывается характер возникновения пластических деформаций бетона в железобетонных балках с большой высотой поперечного сечения. Проводятся расчеты определенного количества толстых балок по нормальным и наклонным сечениям с целью определения зависимости развития пластических деформаций от геометрических параметров балок. Описываются результаты расчета предложенных толстых балок, проводимые в программно-вычислительном комплексе ANSYS Workbench методом конечных элементов. По результатам расчета программы для каждой из балок составлена схема распространения эквивалентных напряжений в теле балки и построен график образования и развития трещин. По полученным расчетным данным можно сформулировать обобщенные выводы относительно образования пластических деформаций в толстых железобетонных балках и плитах, закрепленных по двум противоположным сторонам.
Ключевые слова: толстые железобетонные балки, пластические деформации, пролет среза, распределение напряжений, трещинообразование, напряженно-деформированное состояние.
Форма образования пластических деформаций железобетонных плит и балок большой толщины (высоты поперечного сечения) имеет ряд особенностей, слабо выраженных для обычных железобетонных плит и балок. Охарактеризовать плиту или балку, как толстую или высокую, можно исходя из соотношения ее пролета к высоте сечения (для толстых конструкций l/h < 5 [1]). Иными словами, чтобы определить, является ли балка толстой, необходимо ориентироваться не только на высоту ее сечения, но и на величину пролета, которую данная балка перекрывает.
Далее будут приведены результаты расчетов толстых железобетонных балок, в целях определения зависимости характера образования пластических деформаций, от различных значений пролетов балок относительно их толщины. В таблице 1 приведены основные геометрические и конструктивные параметры балок. Все балки выполнены из бетона класса В30, армированные только нижней продольной арматурой класса А400. По мере возрастания марки балки увеличивается ее длина и пролет, вследствие чего возрастают значения соотношений l/h и a/h0 — отношение пролета к толщине конструкции и пролет среза соответственно. Все рассчитанные балки имеют одинаковый вид расчетной схемы — свободное опирание по двум противоположным концам, и воспринимают сосредоточенную возрастающую нагрузку, приложенную в центре пролета. Общий вид расчетной схемы и схема армирования балок представлены на рисунке 1.
Таблица 1
Характеристики толстых балок
|
№ п/п |
Марка |
Геометрические размеры |
Пролет среза a/h0 |
l/h |
Продольная арматура |
Коэффициент армирования μ, % |
|||||
|
b, мм |
h, мм |
h0, мм |
L, мм |
l, мм |
a=0,5l, мм |
||||||
|
1 |
Б-1 |
250 |
450 |
400 |
400 |
200 |
100 |
0,25 |
0,44 |
4 ø12 А400 |
0,452 |
|
2 |
Б-2 |
250 |
450 |
400 |
600 |
400 |
200 |
0,5 |
0,89 |
4 ø 12 А400 |
0,452 |
|
3 |
Б-3 |
250 |
450 |
400 |
800 |
600 |
300 |
0,75 |
1,33 |
4 ø 12 А400 |
0,452 |
|
4 |
Б-4 |
250 |
450 |
400 |
1000 |
800 |
400 |
1 |
1,78 |
4 ø 12 А400 |
0,452 |
|
5 |
Б-5 |
250 |
450 |
400 |
1200 |
1000 |
500 |
1,25 |
2,22 |
4 ø 12 А400 |
0,452 |
|
6 |
Б-6 |
250 |
450 |
400 |
1400 |
1200 |
600 |
1,5 |
2,67 |
4 ø 12 А400 |
0,452 |
|
7 |
Б-7 |
250 |
450 |
400 |
1600 |
1400 |
700 |
1,75 |
3,11 |
4 ø 12 А400 |
0,452 |
|
8 |
Б-8 |
250 |
450 |
400 |
1800 |
1600 |
800 |
2,0 |
3,56 |
4 ø 12 А400 |
0,452 |
|
9 |
Б-9 |
250 |
450 |
400 |
2200 |
2000 |
1000 |
2,5 |
4,44 |
4 ø 12 А400 |
0,452 |
|
10 |
Б-10 |
250 |
450 |
400 |
2600 |
2400 |
1200 |
3,0 |
5,33 |
4 ø 12 А400 |
0,452 |
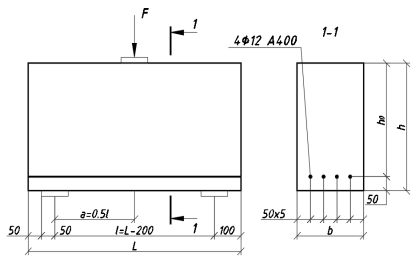
Рис. 1. Схема армирования балок
Толстые железобетонные балки рассчитывались двумя способами: методом расчета, указанным в СП 63.13330.2018 «Бетонные и железобетонные конструкции» [2], и методом конечных элементов (МКЭ) с помощью программно-вычислительного комплекса ANSYS Workbench.
Результаты расчетов балок по нормальным и наклонным сечениям при помощи методов расчета изгибаемых железобетонных элементов, предложенных в СП 63.13330.2018 «Бетонные и железобетонные конструкции» [2], представлены в таблице 2. При этом, предельный изгибающий момент Mult, воспринимаемый нормальным сечением балки, определяется по формуле [2]:
где Rb — расчетное сопротивление бетона сжатию для класса В30 [2];
x — высота сжатой зоны бетона.
Значение внешней сосредоточенной нагрузки Fcr1 соответствует разрушающей силе, которую воспринимает балка при достижении значения изгибающего момента в центре её пролета предельной величины Mult.
Момент трещинообразования Mcrc определен по формуле [2]:
![]() (2)
(2)
где Rbt,ser — нормативное сопротивление бетона растяжению для класса В30 [2];
Wpl — упругопластический момент сопротивления сечения для крайнего растянутого волокна бетона.
В зависимости от марки балки изменяется значение внешней сосредоточенной нагрузки Fcrc, соответствующей моменту трещинообразования Mcrc.
Расчет по наклонным сечениям производился исходя из условия [2]:
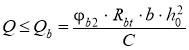 (3)
(3)
где Qb — поперечная сила, воспринимаемая бетоном в наклонном сечении;
φb2 — коэффициент, равный 1,5;
Rbt — расчетное сопротивление бетона растяжению для класса В30 [2];
С — длина проекции наклонного сечения на продольную ось элемента, принимаемая равной не менее h0 и не более 2h0.
Значение внешней сосредоточенной силы Fcr2 соответствует поперечному усилию в наклонном сечении балки, равному Qb.
Таблица 2
Результаты расчетов толстых балок
|
№ п/п |
Марка |
Mult, кН·м |
Fcr1, кН |
Mcrc, кН·м |
Fcrc, кН |
Qb, кН |
Fcr2, кН |
|
1 |
Б-1 |
60,34 |
1206,7 |
20,06 |
401,1 |
172,5 |
345,0 |
|
2 |
Б-2 |
60,34 |
603,4 |
20,06 |
200,6 |
172,5 |
345,0 |
|
3 |
Б-3 |
60,34 |
402,2 |
20,06 |
133,7 |
172,5 |
345,0 |
|
4 |
Б-4 |
60,34 |
301,7 |
20,06 |
100,3 |
138,0 |
276,0 |
|
5 |
Б-5 |
60,34 |
241,3 |
20,06 |
80,23 |
115,0 |
230,0 |
|
6 |
Б-6 |
60,34 |
201,1 |
20,06 |
66,86 |
98,57 |
197,1 |
|
7 |
Б-7 |
60,34 |
172,4 |
20,06 |
57,31 |
86,25 |
172,5 |
|
8 |
Б-8 |
60,34 |
150,8 |
20,06 |
50,14 |
86,25 |
172,5 |
|
9 |
Б-9 |
60,34 |
120,7 |
20,06 |
40,11 |
86,25 |
172,5 |
|
10 |
Б-10 |
60,34 |
100,6 |
20,06 |
33,43 |
86,25 |
172,5 |
Исходя из данных, указанных в таблице 2, можно заметить некоторые закономерности. Расчет конструкций по наклонным сечениям с учетом того, что в балках отсутствует поперечная арматура, указывает на то, что поперечные усилия в балке воспринимаются только бетоном. При этом, для балки Б-1 максимальная величина поперечного усилия, которую может воспринять бетон, составляет 172,5 кН при внешней нагрузке в 345,0 кН, в то время, как значение внешней нагрузки, соответствующее разрушению по нормальному сечению балки и соответствующее трещинообразованию по растянутой зоне балки в центре ее пролета значительно выше (Fcr1 > Fcrc > Fcr2). Исходя из этого, можно сделать вывод, что для балки Б-1 при увеличении внешней нагрузки образование наклонных трещин от точки приложения нагрузки до опоры произойдет раньше появления трещин по растянутой зоне бетона. То есть, разрушение балки Б-1 должно наступить по сжатой зоне бетона по наклонным сечениям.
Для балок Б-2 — Б-6 величина внешней сосредоточенной силы имеет зависимость Fcr1 > Fcr2 > Fcrc, исходя из которой, можно предположить, что в ходе увеличения внешней нагрузки в первую очередь появятся трещины по растянутой зоне бетона, однако, значительное развитие этих трещин не предполагается из-за последующего образования наклонных трещин. При этом, так как Fcr1 > Fcr2 следует предположить, что разрушение балок Б-2 — Б-6 произойдет по сжатой зоне бетона по наклонным сечениям. Также следует отметить, что при увеличении пролета среза с 0,5 по 1,5 разница между значениями внешней нагрузки Fcr1 и Fcr2 резко уменьшается. Исходя из данной закономерности, можно предположить, что в ходе возрастания внешней нагрузки развитие нормальных трещин в растянутой зоне бетона толстой балки будет наиболее выраженным, чем большее значение имеет пролет среза балки a/h0.
В ходе увеличения пролета среза балки до 1,75 и выше (балки Б-7 — Б-10), наблюдается зависимость Fcr2 > Fcr1 > Fcrc, характерная для обычных балок. То есть, при увеличении внешней нагрузки в первую очередь образуются нормальные трещины ближе к центру пролета балки, а разрушение происходит по растянутой зоне бетона. Так как отношение пролета балки Б-10 к её толщине l/h > 5, согласно [1], балка Б-10 уже не является толстой.
На рисунке 2 представлен график зависимости между значением внешней разрушающей нагрузки от величины пролета среза для балок Б-1 — Б-10, наглядно отображающий данные из таблицы 1 и 2. Можно отметить, что при значении пролета среза a/h0 = 1,75 величины разрушающих нагрузок Fcr1 и Fcr2 становятся практически равными, что говорит о том, что форма образования пластических деформаций для балок с a/h0 > 1,75 имеет черты, характерные обычным железобетонным балкам.
На рисунках 3–12 показано распределение эквивалентных напряжений в балках и указаны графики образования и развития трещин, составленные в ходе расчета толстых балок Б-1 — Б-10 при помощи программно-вычислительного комплекса ANSYS.
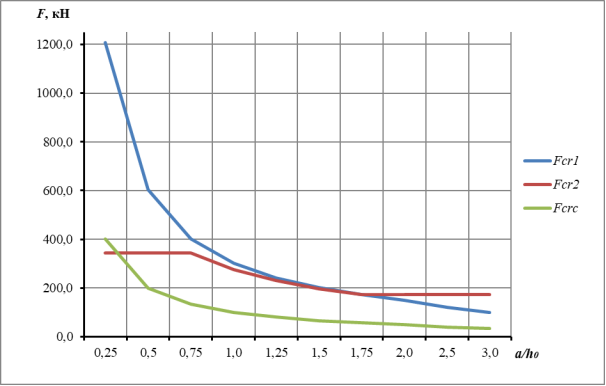
Рис. 2. Графики зависимости величины разрушающей силы от пролета среза
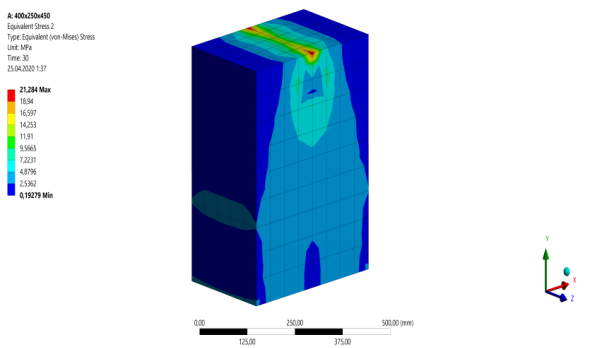
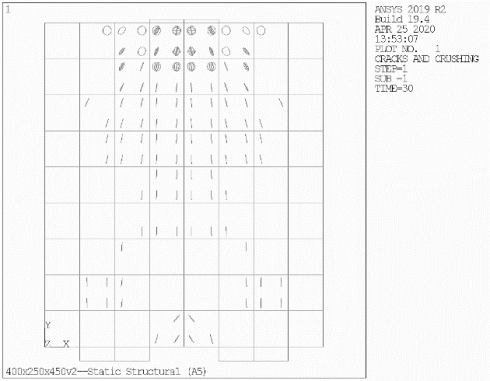
Рис. 3. Разрушение балки Б-1 с пролетом среза a/h0 = 0,25
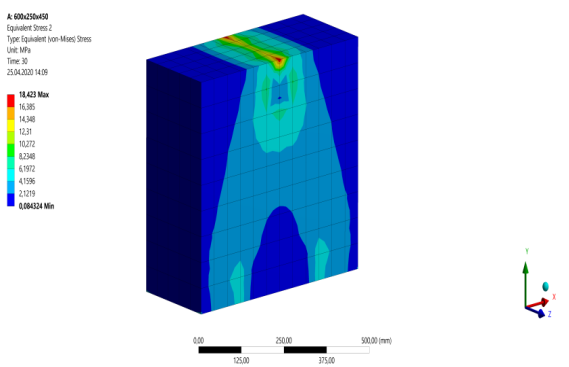
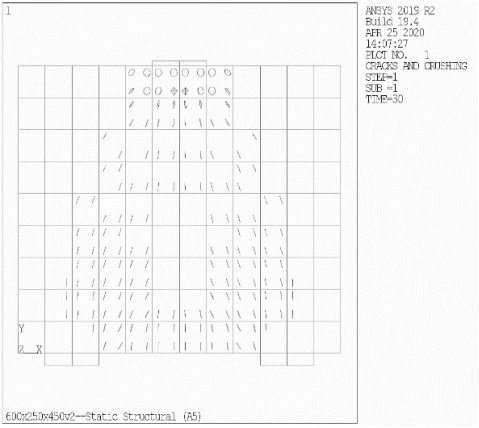
Рис. 4. Разрушение балки Б-2 с пролетом среза a/h0 = 0,5
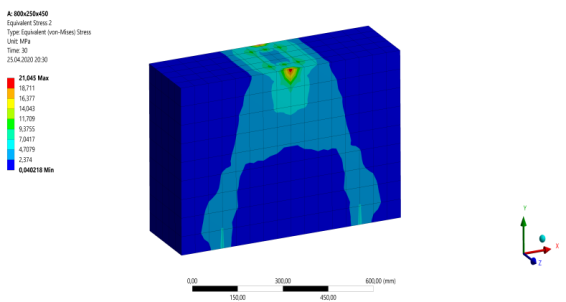
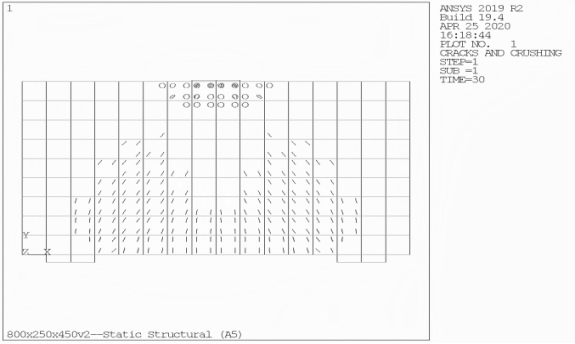
Рис. 5. Разрушение балки Б-3 с пролетом среза a/h0 = 0,75
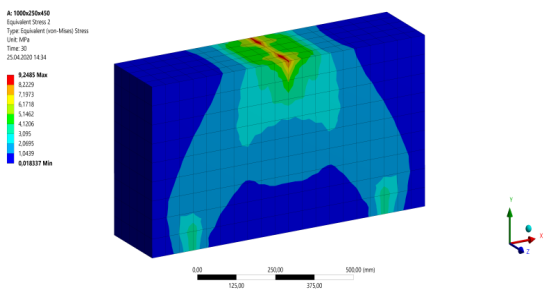

Рис. 6. Разрушение балки Б-4 с пролетом среза a/h0 = 1,0
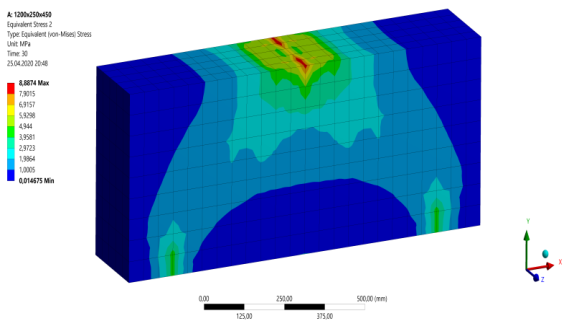

Рис. 7. Разрушение балки Б-5 с пролетом среза a/h0 = 1,25
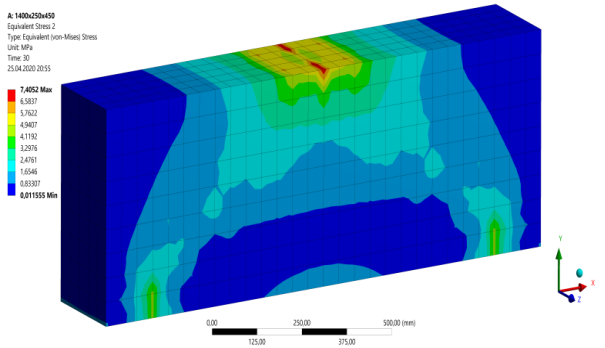

Рис. 8. Разрушение балки Б-6 с пролетом среза a/h0 = 1,5


Рис. 9. Разрушение балки Б-7 с пролетом среза a/h0 = 1,75


Рис. 10. Разрушение балки Б-8 с пролетом среза a/h0 = 2,0
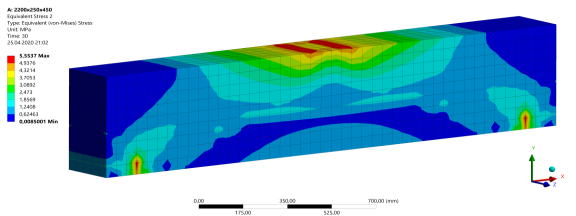
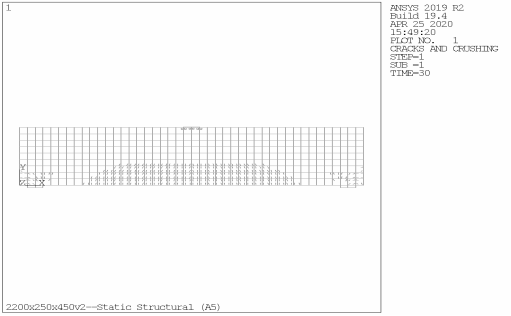
Рис. 11. Разрушение балки Б-9 с пролетом среза a/h0 = 2,0


Рис. 12. Разрушение балки Б-10 с пролетом среза a/h0 = 3,0
По результатам расчетов толстых железобетонных балок Б-1 — Б-10, нагруженных соответствующими сосредоточенными силами, равными Fcr1 и Fcr2, методом конечных элементов можно сделать выводы, подтверждающие закономерности, охарактеризованные расчетами по СП [2]. По формам распространения эквивалентных напряжений в балках заметно, что для более толстых балок с наименьшим пролетом среза наибольшая концентрация напряжений приходится по сжатым «раскосам», в то время как с увеличением пролета среза балок, значения напряжений по нижней растянутой зоне постепенно приближается к значениям в сжатых «раскосах».
График распространения трещин на стадии разрушения балки Б-1 указывает на крайне незначительное развитие нормальных трещин в растянутой зоне бетона и разрушение балки по наклонным сечениям. Для балок Б-2 — Б-6 графики образования трещин также свидетельствуют о разрушении балок по наклонным сечениям (сжатой зоне), при этом в ходе увеличения пролета среза развитие нормальных трещин по растянутой зоне бетона становится более выраженным. Графики балок Б-7 — Б-10 показывают, что для соответствующих балок характерны как развитие наклонных трещин, так и развитие нормальных трещин, при этом с возрастанием марки балки протекание в ней пластических деформаций приобретает черты, все более свойственные обычным балкам.
Обобщая полученные результаты, можно сделать вывод об особенностях развития пластических деформаций в толстых железобетонных балках. При уменьшении пролета среза балок и увеличении их толщины относительно пролета, то есть, классифицируя балки от обычных к толстым, характер образования и развития пластических деформаций бетона изменяется. Это проявляется тем, что распространение нормальных трещин растянутой зоны бетона становится менее выраженным, в то время как трещинообразование по наклонным сечениям проявляется все более интенсивно. Следствием этого является изменение характера разрушения балок — от разрушения балки в центре пролета (в месте приложения максимального изгибающего момента) к разрушению по наклонным сечениям от действия критической поперечной нагрузки. Исходя из этого, можно предположить, что для более толстых конструкций наиболее опасными являются касательные напряжения в приопорных зонах, чем нормальные растягивающие напряжения от действия изгибающего момента.
Литература:
- Палий О. М. Справочник по строительной механике корабля. Часть 2. Пластины. Теория пластичности и ползучести. Численные методы. — Ленинград: Судостроение, 1982. — 464 с.
- СП 63.13330.2018. Бетонные и железобетонные конструкции. Основные положения. СНиП 52–01–2003. М.: НИИЖБ, 2018. — 143 с.
- Пособие по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры (к СП 52–101–2003). ЦНИИПромзданий, НИИЖБ. — М.: ОАО ЦНИИПромзданий, 2005. — 214 с.
- Корнюхин А. В. Экспериментально-теоретические исследования толстых плит: моногр. / А. В. Корнюхин, М. В. Кочеткова, О. В. Снежкина. — Пенза: ПГУАС, 2013. — 132 с.
- Мурашев В. И. Трещиноустойчивость, жесткость и прочность железобетона. Основы сопротивления железобетона. — М.: Машстройиздат, 1950. — 269 с.







