Nanoplasmonics theory in solar cells



In this article, describe nanoplasmonics theory and how to use in solar cells. Besides, we calculate generation rate by nanoplasmonics in some materials.

Key words: nanoplasmonics, solar cell, generation rate, continuity equation

The motion equations of electrons and holes are determined by solving the drift-diffusion equations. These equations are based on the equation of continuity.

J_n=µ_n(n󠄷∇E_c-1.5nkT∇ln(m_n))+D_n(∇n-n∇ln(γ_n)) (1)

J_p=µ_p(n󠄷∇E_v-1.5nkT∇ln(m_p))+D_p(∇p-p∇ln(γ_p)) (2)

Here:

Jn and Jp are the current densities generated by electrons and holes.

µn and µp are the motions of electrons and holes.

mn and mp are the effective masses of electrons and holes.

Dn and Dp are the diffusion coefficients for electrons and holes.

Ec is the energy of the conduction band.

Ev is the energy of the valence band.

k is the Boltzmann constant.

T is temperature

γ_n and γ_p are fermi statistics for electrons and cavities and it is defined as follows for electrons and cavities.

γ_n=N_C^-1n*exp((E_F,n-E_c)*k^-1T^-1) (4)

γ_p=N_v^-1p*exp((E_v-E_F,p)*k^-1T^-1) (5)

Here:

N_c is the density of cases in the conduction band

N_v is the valence zone case density

E_F,n quasi-farm zone energy for n type

E_F,p quasi-farm zone energy for p type

If we use Einstein's relation for electrons and holes, equations 1 and 2 look like this.

D_n=kTµ_n (6)

D_p=kTµ_p (7)

J_n=-nqµ_n∇Φ_n (8)

J_p=-pqµ_p∇Φ_p (9)

Here:

Φ_n and Φ_p are quasi-Fermi potentials for electrons and holes.

We can determine the potentials of a quasi-fermi using Boltzmann statistics.

The electrostatic potential is determined by the Poisson equation.

∇(ε∇φ+P)=-q(p-n+N_D-N_A)-ρ_trap (10)

Here:

ε is the dielectric constant

P is the ferromagnetic polarity.

q is the elementary charge

ρtrap is the charge density due to defects.

φ is electrostatic potential.

If the medium in question is silicon, it is not a ferromagnetic substance and therefore does not have ferromagnetic polarity.

Δφ=-q*ε^-1(p-n+N_D-N_A)- ρ_trap*ε^-1 (10)

The solution of the above equations gives us the volt-ampere characteristic.

Volt-aper characteristic for darkness:

J=J₀*exp(U*q*k^-1T^-1) (11)

Assuming the light is falling:

J=J₀*exp(U*q*k^-1T^-1)-J_ph (12)

Where Jph is the photogeneration current density.

If the nanoparticles introduced into a solar cell represent an increase in its absorption coefficient, then the photogeneration current also changes. That is, it increases [3].

The nanoplasmonic effect can cause 3 different phenomena [2].

1. Nanoparticles radiate light in a visible field due to incident light
2. Or the emission of electrons due to incident light.
3. Converts absorbed energy into heat

We know that the element silicon mainly absorbs light in the visible field. So through this we can increase the absorption coefficient of the solar cell.

The optical properties of solar cells are determined by the transfer matrix method. That is, its absorption, return, and transition coefficients are determined. The rate of generation is determined by the abstract part of the complex refractive index.

G₀= αI(d)h^-1ω^-1 (13)

α=4πkλ^-1 (14)

Here:

G0 is generation rate.

α is the absorption coefficient

k is the abstract part of the complex refractive index

λ is the wavelength

h is the Planck constant

I (d) is the intensity of the incident light.

ω is the cyclic frequency of the incident light.

So, given the nanoplasmonic effect, what frequency and energy does a nanoparticle emit first?

If we say that the share of the radiation phenomenon C_sc, which is visible from the above 3 possible phenomena in the nanoplasmonic effect, then the radiant energy [1].

I(ω)=I₀(ω)*S^-1*C_sc(ω) (15)

Here:

I (ω) is the energy intensity of the radiation

S — πr2 for effective surface nanoparticles

I0 (ω) is the intensity of light incident on the nanoparticle

C_sc(ω)=k⁴(3V)²((ε’_r-1)²+ε_r”²)*((2+ ε’_r)²+ ε_r”²)^-1*(6π)^-1 (16)

Here:

k is the number of waves

V is the volume of the nanoparticle

ε’_r is the true part of the complex dielectric constant

ε_r” is an abstract part of complex dielectric constant

Formula 16 was discovered in 1982 by Bohrenn and Huffman.

So if we combine all this, we can see that the absorption coefficient increases. Along with this, the generation rate also increases.

ΔG=α*N*I₀(d)S^-1C_sch^-1ω^-1 (17)

G_um= ΔG+G₀ (18)

Where N is the number of nanoparticles.

G_ω= I₀(ω) h^-1ω^-1(1+NS^-1C_sc(ω)exp(-αd)) (19)

The general generation is

G_um= ∫I₀(ω) h^-1ω^-1(1+NS^-1C_sc(ω)exp(-αd))δω (20)

So the photocurrent density is

J_ph=q*d*∫I₀(ω) h^-1ω^-1(1+NS^-1C_sc(ω)exp(-αd))δω (21)

So, I-V characteristics

J=J₀*exp(U*q*k^-1T^-1)- q*d*∫I₀(ω) h^-1ω^-1(1+NS^-1C_sc(ω)exp(-αd))δω (22)

All results are taken by “Suntulip -2 for silicon solar cell” simulation program. We can see a result in fig 1. Besides, all results took logarithmic.

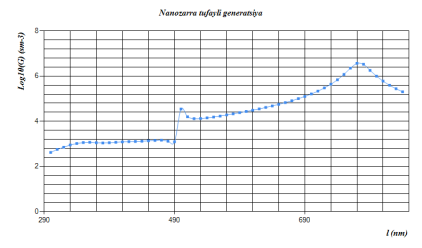
Fig 1. Extra generation by silver nanoparticles

References:

1. M. I. Stockman, Nanofocusing of optical energy in tapered plasmonic waveguides. Phys. Rev. Lett. 93, 137404–1-4 (2004)
2. F. de Angelis, M. Patrini, G. Das, I. Maksymov, M. Galli, L. Businaro, L. C. Andreani, E. Di Fabrizio, A hybrid plasmonic-photonic nanodevice for label-free detection of a few molecules. Nano Lett. 8, 2321–2327 (2008)
3. Carsten Sonnichsen, Plasmons in metal nanostructures, Munching, 20 June 2001.