Статья содержит краткий обзор теории расслоения-связности комбинаторной теории переобучения.
Ключевые слова: ИИ, переобучения, оценка, обобщающая способность, комбинаторная теория.
The article contains a brief review of the bundle-connected theory of the combinatorial theory of overfitting.
Keywords: AI, overfitting, assessment, generalization ability, combinatorial theory.
В теории обучения одной из главных проблем является оценка вероятностей ошибок исходя из семейства алгоритмов, обучающей выборки и метода обучения. Уменьшение количества оценок позволяет создавать алгоритмы, обобщающую способность, которых можно контролировать. В большинстве случаев решения — не оптимальны. При комбинаторном подходе вместо вероятности ошибки оценивается средняя ошибка на неизвестной контрольной выборке, что не меняет сути оценок [3].
Постановка задачи, определения и обозначения приведены в [3].
Оценки вероятности переобучения
Будем полагать, что все алгоритмы из A имеют попарно различные векторы ошибок. Введём на A естественное отношение порядка:
![]()
![]() и
и ![]()
Для постройки отношений между алгоритмами a и b используем метрику. В качестве функции расстояния между векторами ошибок используем хэммингово расстояние, и обозначаем через ![]() .
.
Если ![]() и при этом
и при этом ![]() то будем говорить, что
то будем говорить, что ![]() предшествует
предшествует ![]() и записывать
и записывать ![]() . Очевидно, что
. Очевидно, что ![]() .
.
Графом расслоения–связности множества алгоритмов A будем называть направленный граф ![]() с множеством рёбер
с множеством рёбер ![]()
Граф расслоения–связности является дольным, много-дольным, доли соответствуют слоям алгоритмов ![]() рёбрами могут соединяться только алгоритмы соседних слоёв. Каждому ребру
рёбрами могут соединяться только алгоритмы соседних слоёв. Каждому ребру ![]() соответствует единственный объект
соответствует единственный объект![]() , такой, что
, такой, что ![]() и
и ![]() .
.
Верхней (нижней) связностью алгоритма ![]() будем называть число рёбер графа, исходящих из (входящих в) вершину
будем называть число рёбер графа, исходящих из (входящих в) вершину ![]() , соответственно:
, соответственно:
![]()
![]()
Связность есть реализуемое семейством ![]() число способов изменить алгоритм a так, чтобы он стал делать на одну ошибку больше (или меньше). Связность можно интерпретировать как число степеней свободы семейства
число способов изменить алгоритм a так, чтобы он стал делать на одну ошибку больше (или меньше). Связность можно интерпретировать как число степеней свободы семейства![]() в локальной окрестности алгоритма
в локальной окрестности алгоритма ![]() . Для семейства линейных классификаторов значение связности концентрируется вокруг значения размерности пространства [4].
. Для семейства линейных классификаторов значение связности концентрируется вокруг значения размерности пространства [4].
Не оптимальностью
![]() .
.
Другими словами, ![]() есть число различных объектов
есть число различных объектов ![]() , соответствующих всевозможным рёбрам
, соответствующих всевозможным рёбрам ![]() на путях, ведущих к вершине
на путях, ведущих к вершине ![]() .
.
В общем случае ![]() . Равенство
. Равенство ![]() достигается на всех алгоритмах двух самых нижних слоёв. Равенство
достигается на всех алгоритмах двух самых нижних слоёв. Равенство ![]() достигается в случае, когда существует корректный алгоритм
достигается в случае, когда существует корректный алгоритм ![]() .
.
Оценка расслоения–связности: Теорема.
Определим для всех ![]() функцию гипергеометрического распределения:
функцию гипергеометрического распределения:
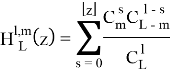
Пусть ![]() метод минимизации эмпирического риска, векторы ошибок всех алгоритмов из
метод минимизации эмпирического риска, векторы ошибок всех алгоритмов из ![]() попарно различны. Тогда для любого
попарно различны. Тогда для любого ![]() .
.
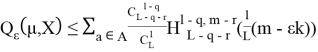 ,
,
где ![]() верхняя связность и не оптимальность алгоритма a соответственно,
верхняя связность и не оптимальность алгоритма a соответственно, ![]()
Рассмотрим основные свойства данной оценки.
1. Комбинаторный множитель
Во-первых, связные множества алгоритмов менее подвержены переобучению. Это относится широкому классу параметрических семейств алгоритмов классификации, у которых разделяющая поверхность непрерывна по параметрам.
Во-вторых, лишь несколько нижних слоёв вносят существенный вклад в переобучение. Это позволяет вычислять приближённые (нижние) оценки ![]() , перебирая алгоритмы по слоям снизу вверх. Из-за того, что в нижних слоях находится обычно очень малое количество алгоритмов, то оценки могут быть эффективно вычислены.
, перебирая алгоритмы по слоям снизу вверх. Из-за того, что в нижних слоях находится обычно очень малое количество алгоритмов, то оценки могут быть эффективно вычислены.
-
Если пренебречь расслоением и связностью, положив
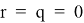 для каждого
для каждого 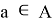 , то получится оценка Вапника–Червоненкиса (при
, то получится оценка Вапника–Червоненкиса (при 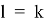 ):
):
![]() .
.
- Оценка расслоения–связности является достижимой. Она обращается в равенство в случае специальных модельных семейств алгоритмов монотонных цепей и многомерных сетей.
Литература:
- Игнатьев Н. А. Обобщенные оценки и локальные метрики объектов в интеллектуальном анализе данных. Ташкент: Университет, 2014. C. 68–72.
- Мадрахимов III.Ф., Саидов Д. Ю. Устойчивость объектов классов и группировка признаков // Проблемы вычислительной и прикладной математики. 2016. № 3 (5). С. 50–55.
- Воронцов К. В. Комбинаторный подход к оценке качества обучаемых алгоритмов // Математические вопросы кибернетики / Под ред. О. Б. Лупа-нова. М.: Физматлит, 2004. Т. 13. С. 5–36.
- Кочедыков Д. А. Структуры сходства в семействах алгоритмов классификации и оценки обобщающей
- Воронцов К. В. Комбинаторная теория переобучения: результаты, приложения и открытые проблемы // Всероссийская конференция «Математические методы распознавания образов». Петрозаводск, 2011 г. C.:2–7.







