В статье приводится постановка задачи и основные особенности моделирования динамики нагретой частице в идеальном газе для одномерного и двумерного случаев. Рассматриваются результаты физико-математического моделирования и их графическое представление.
Ключевые слова: идеальный газ, пылевая плазма, аккомодация атома, физическое моделирование.
В последнее время наблюдается растущий интерес к исследованию пылевой плазмы. Пылевая плазма имеет ряд применений в промышленности. Одной из важных свойств пылевой плазмы является лазерный индуцируемый фазовый переход в монослое полимерных частиц, левитирующих в газоразрядной плазме [1, 2], который объясняется рядом гипотез, в том числе влиянием фотофоретической силы на полимерные частицы.
Предполагается, что фотофоретическая сила возникает из-за модификации поверхности полимерной частицы под действием лазерного излучения. Для проверки этой гипотезы необходимо создать модель, описывающую динамику янус-частицы. Предполагается создание модели янус-частицы, имеющей две поверхности с различными свойствами, причем площади этих поверхностей должны быть равны. Создание такой модели проводится в несколько этапов, из которых автором уже реализовано два. На первом этапе была разработана одномерная модель динамики нагретой частицы в идеальном газе, на втором — двумерная модель рассматриваемой частицы. Базовые принципы динамики частицы в идеальном газе рассмотрены в [3]. В авторской модели, наряду с классическим упругим взаимодействием частицы с атомом, рассматривается взаимодействие с аккомодацией атома на поверхности частицы и последующим отрывом при выполнении ЗСИ.
Частица в одномерном и двумерном случаях рассматривалась в нескольких вариантах локализации:
– бесконечно узкая и глубокая потенциальная яма;
– разрешенная область с зеркальным отражением частицы от границы этой области;
– сила, пропорциональная отклонению частицы от центра расчетной области.
При создании совокупности моделей рассматривалось упругое взаимодействие или взаимодействие с аккомодацией и последующим отрывом атома от поверхности частицы. Размер расчетной области был выбран меньше длины свободного пробега атомов, для того чтобы не учитывать межатомное взаимодействие. В случае упругого взаимодействия частицы с атомом выполняется ЗСИ и ЗСЭ. Для расчета новых скоростей частицы и атома использовались следующие формулы:
|
|
(1) |
|
|
(2) |
где V и V’- скорости частицы до и после столкновения, соответственно, v и v’ — скорости атома до и после столкновения, m — масса атома, M — масса частицы.
В случае аккомодации атома на поверхности частицы с последующим отрывом, выполняется только ЗСИ. Скорость атома при отрыве от частицы определяется согласно распределению максвелла для температуры поверхности частицы. Скорости частицы после аккомодации атома определяется по формуле:
|
|
(3) |
где m — масса атома, M — масса частицы, V и v — скорость частицы и атома до аккомодации атома, V’- скорость частицы после аккомодации атома на поверхности частицы.
Скорость атома и частицы после отрыва определяется по формулам:
|
|
(4) |
|
|
(5) |
где ![]() - скорость атома при отрыве от частицы в системе отсчета частицы, разыгрывается с помощью распределения Максвелла для температуры поверхности частицы.
- скорость атома при отрыве от частицы в системе отсчета частицы, разыгрывается с помощью распределения Максвелла для температуры поверхности частицы.
В двумерном варианте необходимо учитывать нецентральные столкновения частицы с атомом. Схема такого столкновения представлена на рис. 1.
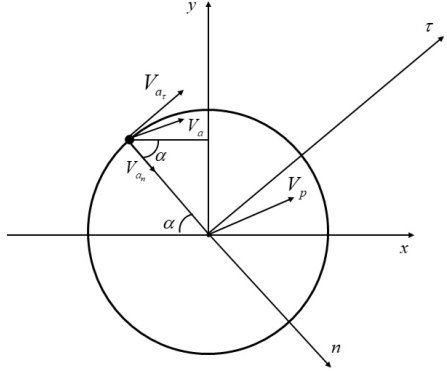
Рис. 1. Схема столкновения атома и частицы
Экспликация: (x, y) — начальные оси координат; (![]() , n) — нормальная и тангенциальные оси(относительно атома);
, n) — нормальная и тангенциальные оси(относительно атома); ![]() ,
, ![]() - тангенциальная и нормальная компонента скорости атома;
- тангенциальная и нормальная компонента скорости атома; ![]() - скорость атома;
- скорость атома; ![]() -скорость частицы;
-скорость частицы; ![]() - угол между координатными осями (x, y) и (
- угол между координатными осями (x, y) и (![]() , n)
, n)
При таком столкновении необходимо перейти к тангенциальной и нормальной оси, для этого достаточно повернуть ось на угол ![]() . При столкновении меняется только нормальная компонента скоростей атома и частицы по формулам (1–2) или (3–5) в зависимости от выбранного взаимодействия.
. При столкновении меняется только нормальная компонента скоростей атома и частицы по формулам (1–2) или (3–5) в зависимости от выбранного взаимодействия.
Для проведения расчетов в рамках рассматриваемых моделей, был разработан комплекс программ в пакете MATLAB. Для определения момента времени, когда началось стационарное состояние, использовался график зависимости соотношения температуры частицы от времени к температуре атомов. Средняя кинетическая энергия частицы от времени определялась через среднюю кинетическую энергию частицы ![]() :
:
|
|
(6) |
График соотношения температур частицы от температуры атомов представлен на рис.2.
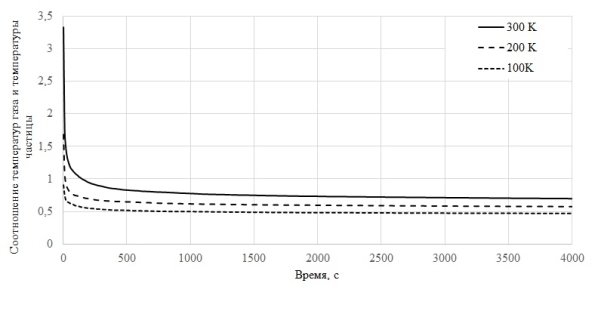
Рис. 2. График зависимости соотношения температуры газа и температуры частицы от времени
Особенностью модели с локализацией в бесконечно узкой и глубокой яме является отсутствие заметания частицей атомов газа, поэтому температура частицы оказалась вдвое меньшей по сравнению с другими вариантами локализацией.
На основе расчетов был проведен анализ зависимости соотношения отношения энергий частицы и атомов для разного соотношения температур поверхности частицы и окружающего газа; пример этой зависимости для одномерного и двумерного случаев, представлен на рис. 3.
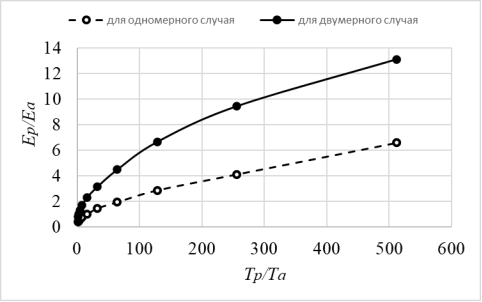
Рис. 3. Зависимость соотношения энергии частицы в энергии атомов от соотношения температур поверхности частицы к температуре атома
Результаты проведенного физико-математического моделирования: в процессе исследования было установлено, что рост энергии частицы уменьшается при увеличении соотношения ![]() для одномерного и двумерного случаев. Диапазон соотношений
для одномерного и двумерного случаев. Диапазон соотношений ![]() , рассмотренный в процессе численного исследования, соответствует используемому диапазону в рамках технически
, рассмотренный в процессе численного исследования, соответствует используемому диапазону в рамках технически
В дальнейшем планируется исследовать поведение двумерной частицы с учетом ее вращения, а также исследовать частицу с несколькими различными поверхностями.
Литература:
- Kononova E. A., Vasilieva M. M., Petrova O. F. Laser-Induced Phase Transition in a Monolayer of Polymer Particles Levitating in a Low-Pressure Gas-Discharge Plasma / / Journal of Experimental and Theoretical Physics, 2018, Vol. 126, No. 5, pp. 600–603.
- Petrov O. F., Vasiliev M. M., Vaulina O. S. et al., Solid-hexatic-liquid transition in a twodimensional system of charged dust particles, EPL, Vol.111, I.4, р. 45002, 2015
- Boris A.Yu., Galkin V. S. Kinetic description of Brownian movement of heated particles in rarefied gas// Fluid Dynamics volume 21, pages302–306(1986)







