Разработка нестандартного интегрированного урока для учащихся XI класса на тему «Решение стереометрических задач с Cabria 3D»



В статье представлена разработка интеграция уроков математики и информатики, на основе компонентов которых строится урок включающий в себя эстетическое воспитание. Для учащихся, представлены задачи различных типов и их разбор с помощью взаимодействия с программой помогающей создавать точные и эстетически привлекательные чертежи.

Ключевые слова: эстетическая культура, модель, стереометрия.

Неизбежность внедрения процессов информатизации и цифровизации образования ставит перед каждым учителем актуальную цель, которая включает в себя освоения компьютерных средств как нового инструмента организации организации обучения с целью повышения мотивации школьников и их познавательного интереса, учучшение содержания предмета и открытие новых видов его освоения. Стереометрия является одним из тех разделов математики, который вызывает у обучающихся трудности при решении задач, выявлении отдельных элементов чертежа. Именно при обучении стереометрии учителя используют различные модели фигур, будь то, каркасные или телескопические модели и даже комбинированные конструкции, которые включают и развертку фигур и наборы для сбора различных многогранников поэтому очевидно, что использование компьютерных средств будет наиболее эффективно в данной области. На основе данной мысли можно придти к выводу о том, что для эффективности усвоения знаний на уроках стереометрии важно использовать интегрированные уроки, связывая такие предметы как геометрия и информатика. С помощью готовых интерактивных моделей, продемонстрированных на интерактивных панелях (досках) можно иллюстрировать геометрические фигуры, доказывать теоремы, определять сечения и многое другое. Но все же есть ряд задач, для решения которых использование готовых чертежей неуместно. К примеру, задачи на построение сечений, углов, расстояний, где в первую очередь нужно сообразить как устроены рассматриваемые в них элементы. В данном контексте для использования подразумеваются программы, использующие виртуальное трехмерное моделирование и контруирование, реализующие интерактивность для учащихся. Итак, продемонстрируем данный урок стереометрии с использование интерактивных ресурсов информатики. Для формирования эстетической культуры обучающихся вспомним, что говорилось о модели использования геометрических задач. При использовании цифровых ресурсов для решения задачи так же можно выявить как внешнюю, так и внутренюю эстетику.

Целью урока является формирование эстетической культуры учащихся.

Задачи урока:

− сформировать умения различать виды геометрических задач;

− сформировать умения работать а программах Cabri 3D и Geogebra;

− рассмотреть решение задач на различных уровнях развития эстетического воспитания.

Тип урока: объяснительно иллюстративный с элементами интеграции.

Ход урока

Актуализация знаний. На данном этапе урока стоит вспомнить с учащимися основные понятия относящиеся к теме урока. Так же провести небольшой инструктаж по программам, которые будут использоваться на уроке.

Решение задач с помощью программы Cabri 3D. Рассмотрим задачу с эстетически привлекательной формулировкой и не менее привлекательным чертежом.

Задача 1. ABCD — ромб, О — точка пересечения диагоналей, М — точка пространства, не лежащая в плоскости ромба. Точки A, D, O лежат на плоскости α. Вычислить площадь ромба, если сторона его равна 4 см, а угол равен 60^°. Предложите различные способы вычисления площади ромба.

Учащимся предлагается сделать чертёж к задаче, но уже не в тетрадях, а в программе. Составление чертежа сопровождается комментариями учителя (рисунок 1, a).

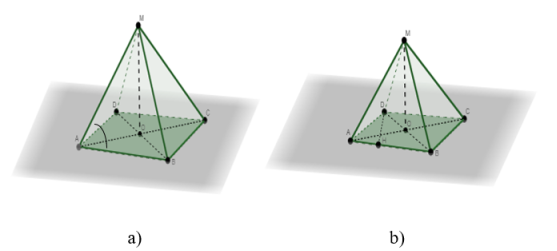
Рис. 1. Чертеж к задаче 1

Решение: 1) В ходе выполнения чертежа предлагается ответить на вопросы:

1. Лежат ли в плоскости α точки В и С?

На данный вопрос учащиеся смогут сразу ответить рассмотрев чертеж в программе с разных ракурсов

2. Лежит ли в плоскости МОВ точка D?

OB ∈ MOB, D∈OB, то D∈MOB

3. Назовите линию пересечения плоскостей MOB и ADO.

O∈MOB, O∈ADO⇨MOB∩ADO=BO, но так как BO — часть DB, то MOB∩ADO=DB

Учитель должен обратить внимание учащихся на тот факт, что если 2 плоскости имеют общие точки, то они пересекаются по прямой, проходящей через эти точки.

4. По какой формуле можно найти площадь ромба?

Ответ на этот вопрос можно дать несколькими способами, что и требуется сделать по условию задачи

1. способ. 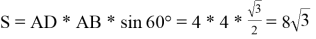(см²) (по квадрату стороны и синусу угла между сторонами)
2. способ. Нахождение площади через высоту и сторону ромба, поэтому достроим высоту на основании пирамиды ABCDM (рисунок 1, b)

Так как высота неизвестна, сначала нужно ее найти.

1) ∠A=60°, AD=4, ∠DHA=90° ⇨ ∠ADH=30°, тогда катет AH=

2) Так как известен один из катетов и гипотенуза, то DH=

3) Так как DH=, AD=4 ⇨ (см²)

Таким образом в этой задаче можно увидеть не только простоту решения и чертежа, но и различные способы решения задачи. У учащихся в результате решения представленой задачи, формируются: чувственно эмоциональный компонент эстетического воспитания, где учащиеся могут самостоятельно определить внешне эстетически привлекательную задачу

Следующая задача прикладного типа, используется на прикладном уровне.

Задача 2. Египтяне, построив четырехугольную правильную пирамиду с высотой h через точку на боковом ребре, лежащую на расстоянии от плоскости основания, построили еще один уровень внутри в виде плоскости, параллельной плоскости основания, которая отсекает от пирамиды меньшую пирамиду. Найдите объем полученной меньшей пирамиды, если объем исходной пирамиды равен 54.

Снова составим рисунок с помощью программы (рисунок 2, a).

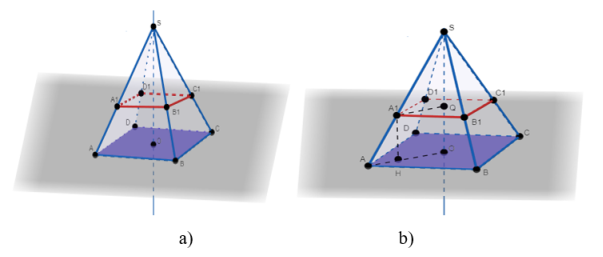
Рис. 2. Правильная пирамида к задаче 2

Решение: Пусть плоскость провели через точку А₁ на ребре AS.

1) Так как эта плоскость параллельна плоскости основания, то она пересекает боковые грани по прямым A₁B₁, B₁C₁,C₁D₁, D₁A₁, параллельным соответственно AB, BC, CD, DA, причем SA₁B₁C₁D_{1 —} тоже правильная четурехугольная пирамида

2) Рассмотрим плоскость ASO. Проведем (SO — высота исходной пирамиды) ⇨ , значит расстояние равно , на котором от плоскости основания проведена плоскость A₁B₁C₁D₁ (рисунок 3, b)

3) Следуя из пункта 3, ⇨⇨ ⇨

4) Из 4 пункта следует, что SQ=⇨∆ASB∼∆A₁SB₁⇨ ⇨

5) ⇨

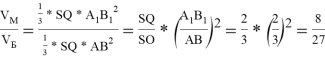Ответ: 16

В данной задаче использовался метод дополнительных построений. Для учащихся эффективно использовать прикладные задачи, так как на данном уровне развивается чувство прекрасного и ощущается взаимосвязь с реальным миром и реальными представлениями объекта, выбор тех или иных признаков обосновывается целесообразностью математического объекта, а программа 3D редактора помогает учащимся увидеть объект с разных ракурсов и разглядеть принадлежность элементов той или иной плоскости.

Следующий, процессуальный уровень, связан с задачами которые уже имеют внутренний эстетический аспект, то есть, используются задачи, которые имеют красивый способ или метод решения. Разберем одну из таких задач.

Задача 3. Основание шестиугольной пирамиды SABCDEF — правильный шестиугольник ABCDEF. Точка M — середина ребра BC.

а) Постройте прямую пересечения плоскостей FSM и ASB.

б) В каком отношении плоскость FSM делит отрезок, соединяющий точку A с серединой ребра SD?

Для начала, стоит привлечь внимание учащихся на том, что пирамида не обязательно правильная, поэтому рассмотрим общий случай, неправильную пирамиду. Первое, что нужно сделать это построить чертеж с помощью уже ранее использованной програмы, снова с коментариями для учащихся (рисунок 3, a)

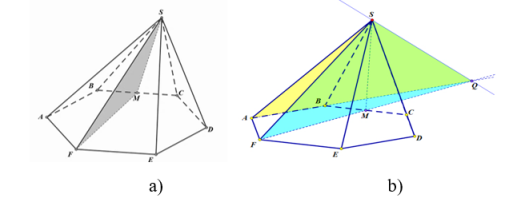
Рис. 3. Чертеж шестиугольной пирамиды SABCDEF

а) 1) Построим линию пересечения плоскостей: проведем прямую FM∈SFM, FM∈ABCDEF, проведем прямую AB∈ASB, AB∈ABCDEF

2) Прямые FM ∩AB в точке Q, точка Q∈FSM, Q∈ASB, аналогично, точка S∈FSM, S∈ASB, поэтому линия пересечения плоскостей может быть проведена через S и Q. Посмотрим как будут выглядеть обе плоскости, попросим учащихся закрасить полученные сечения(рисунок 3, b)

Теперь рассмотрим второй пункт.

б) Построим середину ребра SD с точкой A (рисунок 4, a)

Построим точку, где AP пройдет через плоскость FSM. Для этого построим проекцию AP в плоскости основания — это будет прямая AD. Далее определим точку пересечения AD и FM, ею является точка L, теперь соединим L с точкой S, пересечение LS и AP есть точка прокола (рисунок 4, b). Следующая задача — это определить отношение отрезков AN и NP, для этого определим положение точки L.

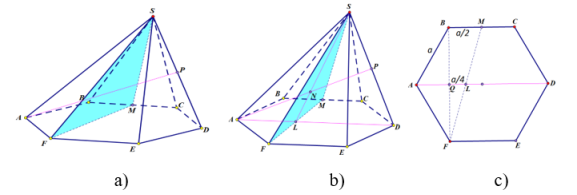
Рис. 4. Построение середины ребра SD

Развернем чертеж так, чтобы было видно только основание, с посощью интсрумента в программе Cabri 3D (рисунок 4, c)

∆BMF∼∆FQL (коэфициэнт подобия равен 2) ⇨. Обозначим сторону основания пирамиды за ɑ и получим

Вернемся в программу и рассмотрим элементы полученного чертежа подетально, для решения следующего этапа задачи(рисунок 5).

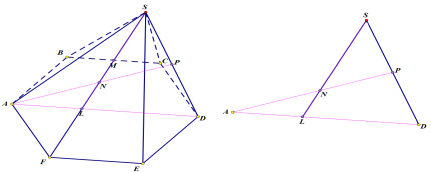
Рис. 5. Чертеж в деталях

На основе разобранных элементов чертежа можем применить теорему Минелая:. Так как

Отсюда получаем ответ , но у данной задачи есть еще один не менее красивый способ решения, рассмотрим и его. В представленной задаче процессуального уровня обоснование базируется на критериях эстетической привлекательности процесса решения задачи, что и было сделано при ее решении.

Следующий уровень, теоретический, подразумевает решение задач, где присутствуют эстетически привлекательные задачи с использованием обобщения и выдвижения гипотез.

Задача 4. Песочные часы состоят из двух одинаковых усеченных конусов, плоскости оснований которых параллельны. Высота песочных часов H=16. Радиус окружности, являющейся пересечением боковых поверхностей конусов, равен 1. Тангенс половины угла раствора каждого конуса равен. Найдите объем песочных часов V, умноженный на .(рисунок 6, a)

Изобразим чертеж к данной задаче с помощью инструментов использвемой нами программы

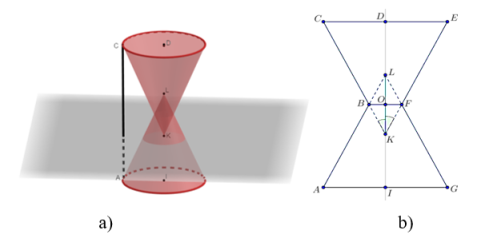
Рис. 6. Изображение песочных часов и их сечение с помощью программы Cabri3D

Рассмотрим сечение конусов плоскостью α, проходящей через их общую ось вращения (рисунок6, b)

1) На рисунке в плоскости α: DI — ось вращения конусов, отрезок DI совпадает с высотой песочных часов и равен 16.

2) Отрезки CD и DE являются радиусами окружности, лежащей в верхнем основании фигуры, а отрезки BO и OF являются радиусами окружности пересечения конусов, отсюда следует BO=OF=1.

3) Угол верхнего конуса ∠CKE делится пополам осью вращения на равные углы , поэтому .

4) Рассмотрим и Плоскости оснований конусов и плоскость, содержащая окружность пересечения конусов, параллельны друг другу ⇒ рассматриваемая плоскость сечения α будет пересекать эти плоскости по прямым, параллельным друг другу ⇒ ⇒ .

5) Ось вращения перпендикулярна плоскостям оснований и плоскости пересечения конусов ⇒ △CKD и △BKO — прямоугольные треугольники.

6) Так как

7)

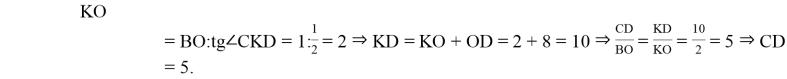
8) Объем усеченного конуса CBOFEDC можно посчитать как разность объемов конуса KCDE и конуса KBOF:

.

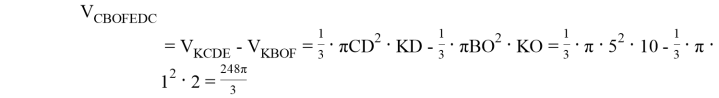9) Объем песочных часов складывается из двух объемов усеченного конуса, так как ситуация с нижним конусом полностью аналогична ситуации с верхним конусом в силу симметрии задачи, поэтому их объемы совпадают объем песочных часов равен V=2⋅.

10) Помножим на получаем: V=2⋅496. Ответ: 496

На основе представленной задачи можно предложить учащимся составить задачу обратную данной или с каким-либо неизвестными компонентами, тем самым, развивая у учащихся логическое мышление. В данной задаче, обусловленной теоретическим уровнем, представлена цепочка умозаключений, которые привели к желаемому результату.

Таким образом, при решении задачи с использованием вспомогательных электронных средств, у учащихся в результате решения представленых задач, формируются три основных компонента: чувственно — эмоциональный, где основным объектом привлекательности является сама формулировка задачи и чертеж, рациональный обоснование ее эстетической привлекательности и деятельностный, который способствует созданию чертежа к рисунку или решению задачи эсетически привлекательным способом или методом, выбранным и обоснованным на базе рационального компонента.

Литература:

1. Мамедяров, Д. М. Эстетическое воспитание учащихся на уроках математики / Д. М. Мамедяров. — Текст: непосредственный // Личность, семья и общество: вопросы педагогики и психологии: сб. ст. по матер. XLIX междунар. науч.-практ. конф.. — 2015. — № 2. — С. 49.
2. Белошистая Задачи на построение в школьном курсе геометрии / Белошистая, В. А. — Текст: непосредственный // Математика в школе. — 2002. — № 9. — С. 47–50.
3. Загвязинский, В. И. Исследовательская деятельность педагога: учеб.пособие / В. И. Загвязинский. — М.: Академия, 2008. — 176 с.
4. Саранцев, Г. И. Как сделать обучение математике интересным: кн. для учителя / Г. И. Саранцев. — М.: Просвещение, 2011. — 160 с.
5. Саранцев, Г. И. Обучение математическим доказательствам и опровержениям в школе [текст] / Г. И. Саранцев. — М.:Владос, 2005. — 183с.