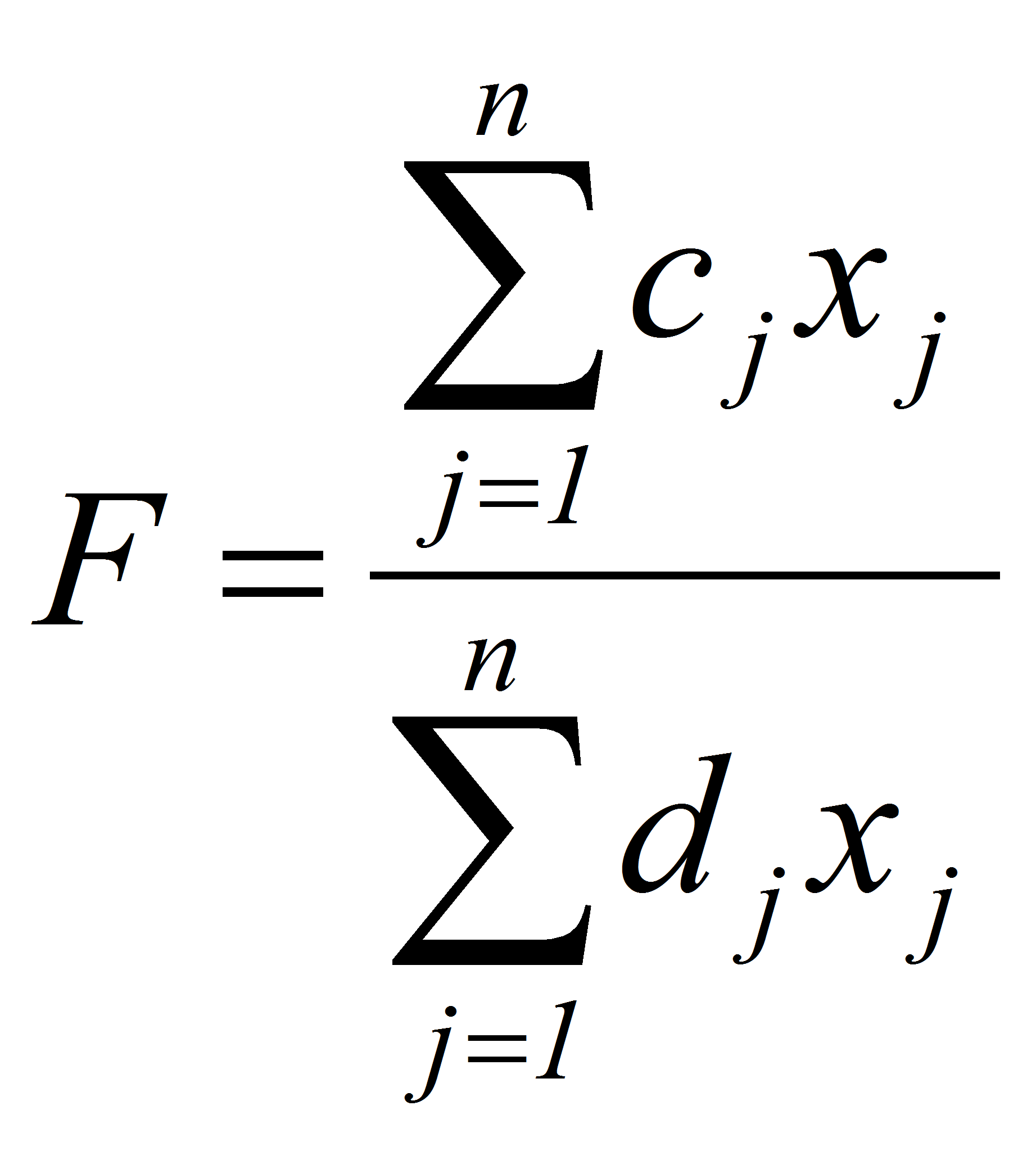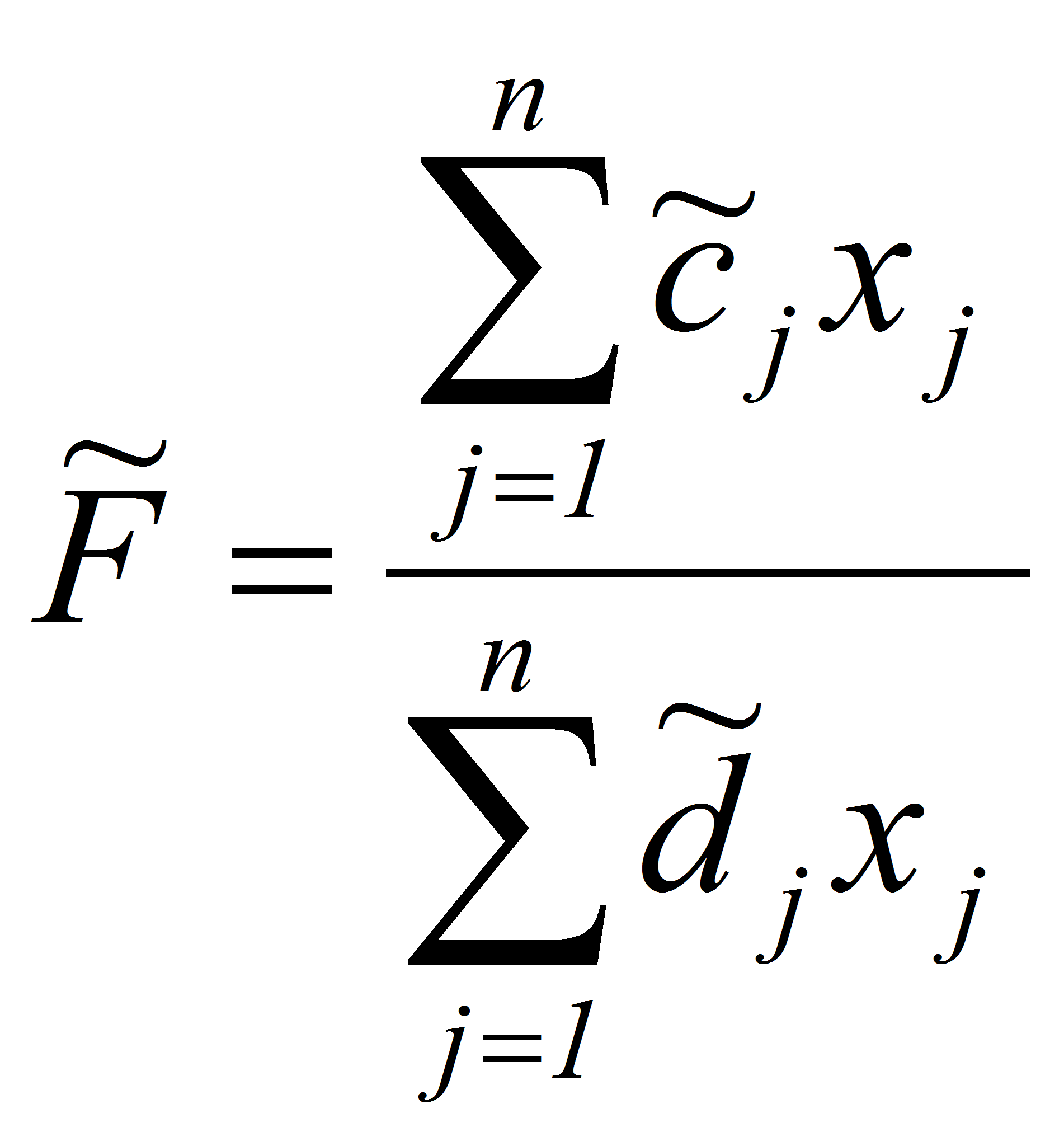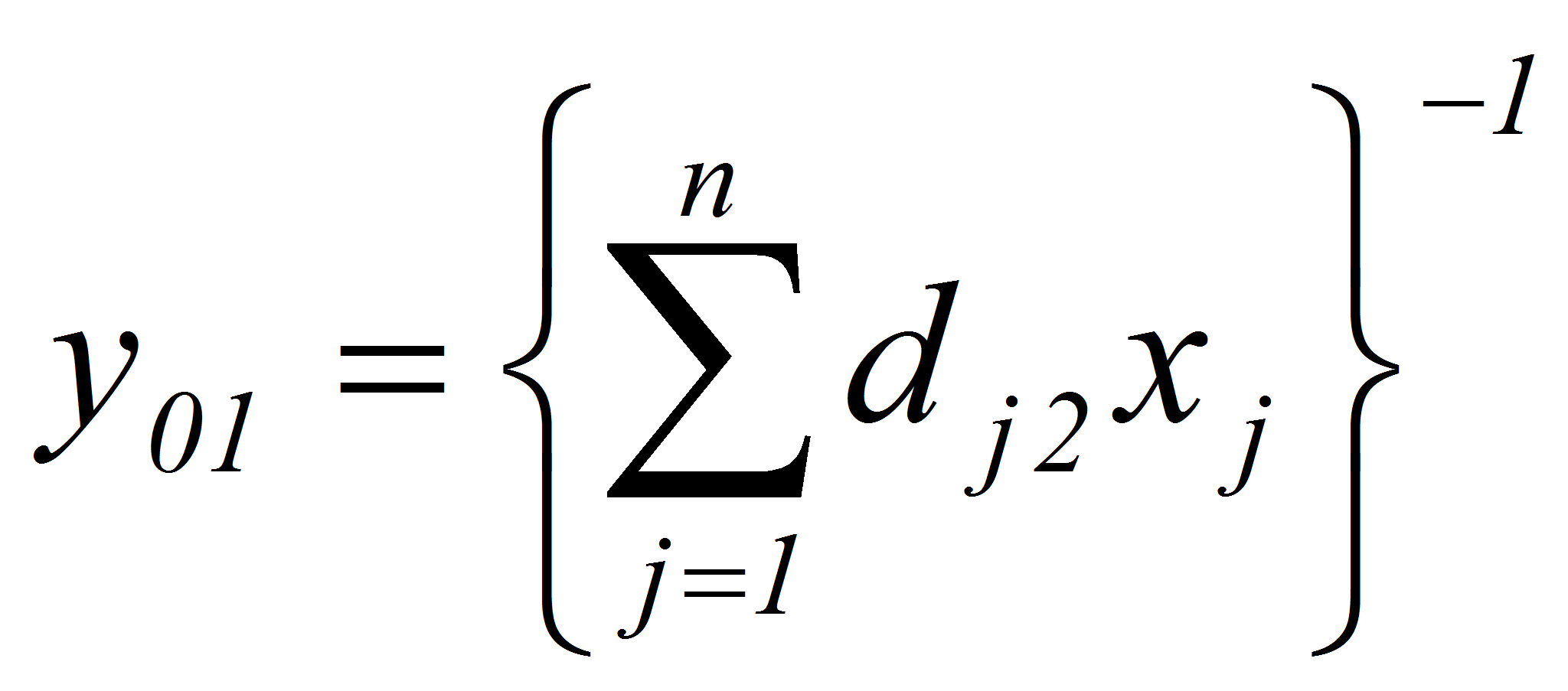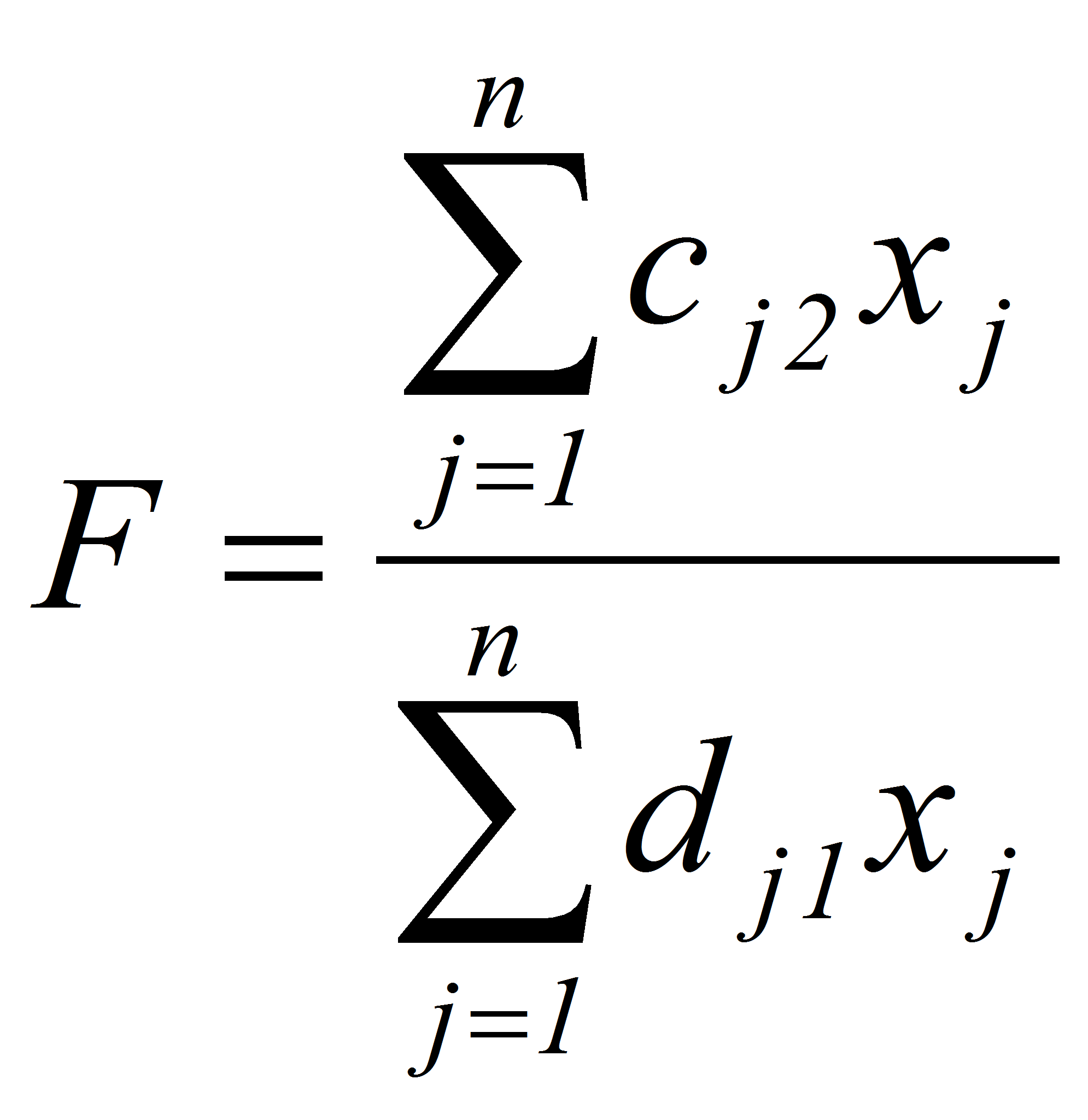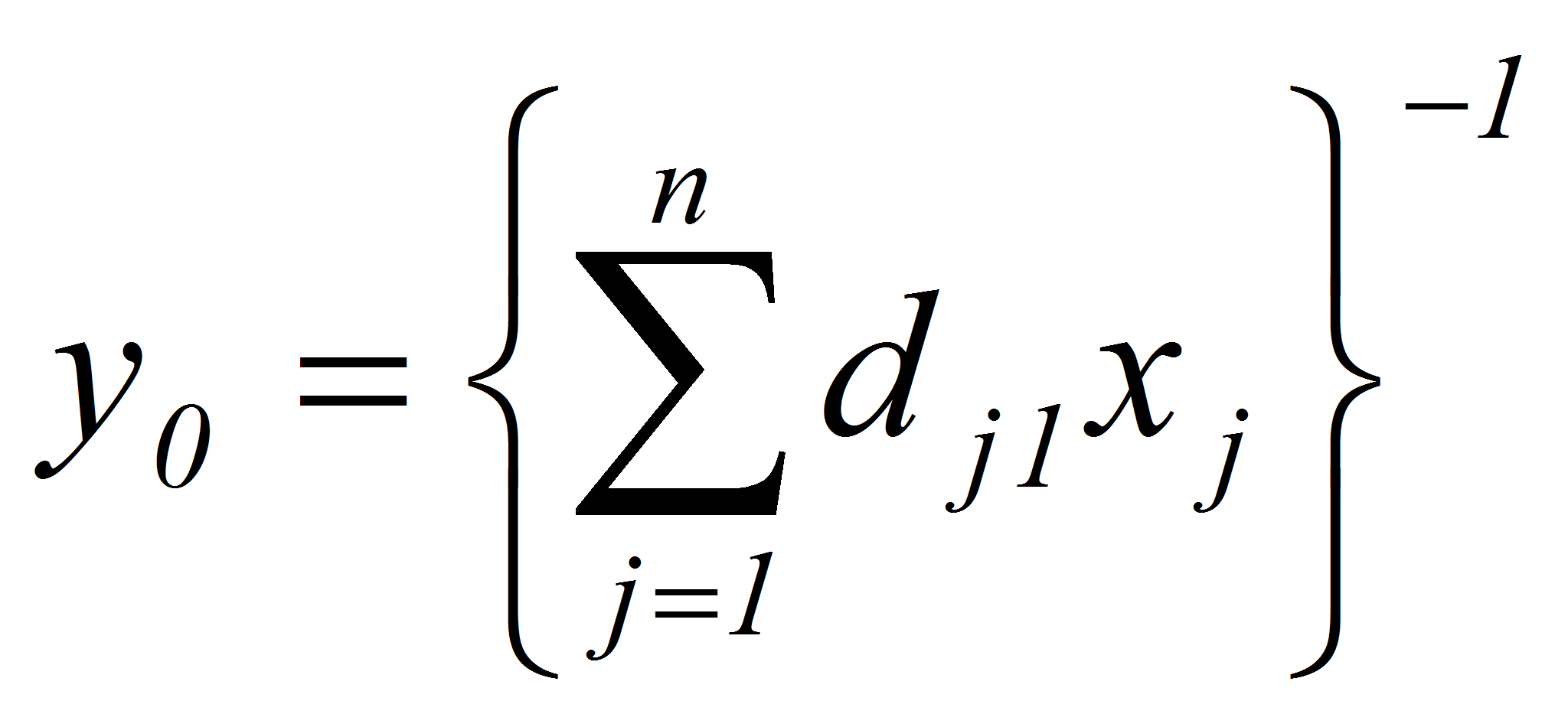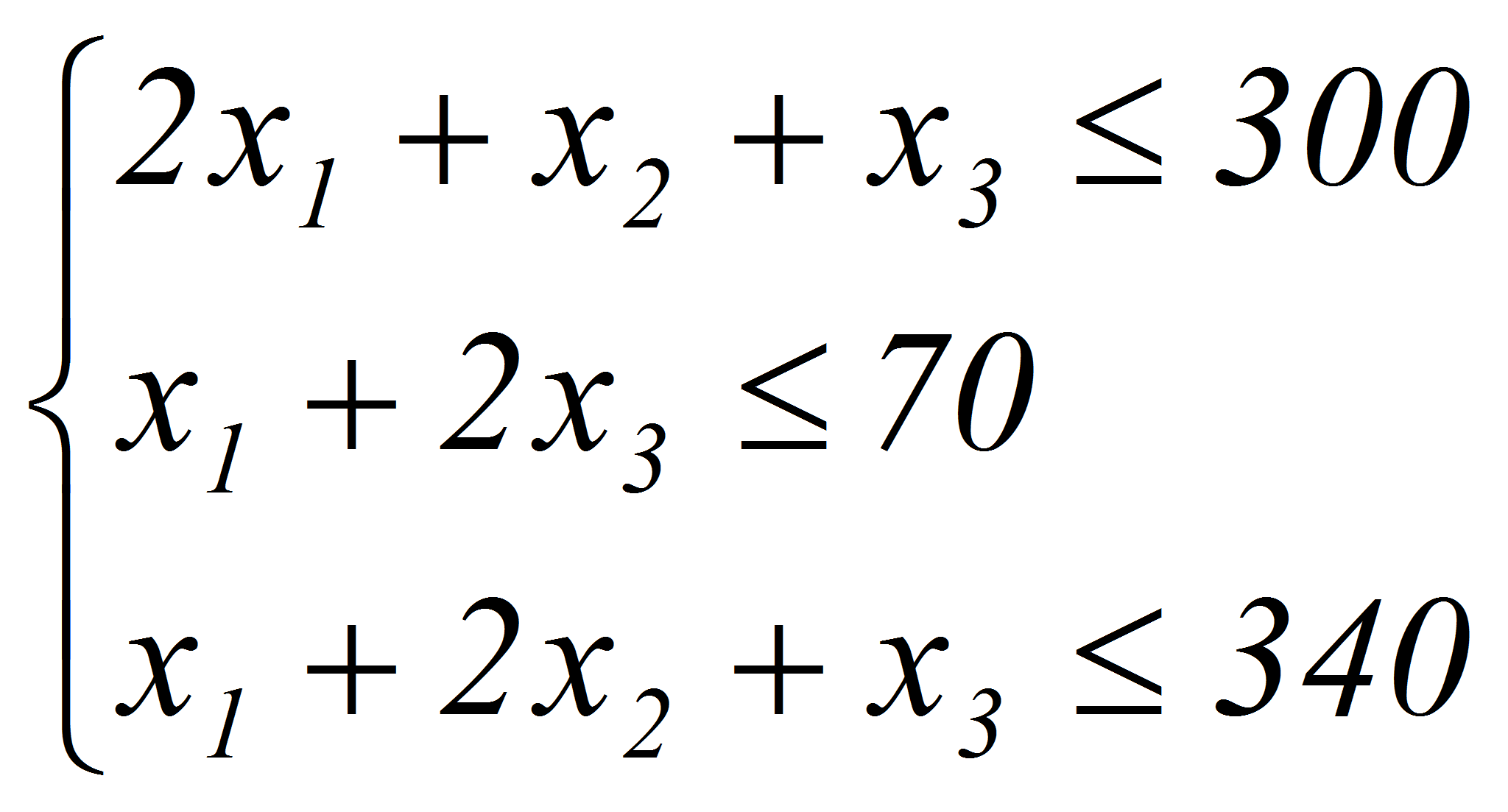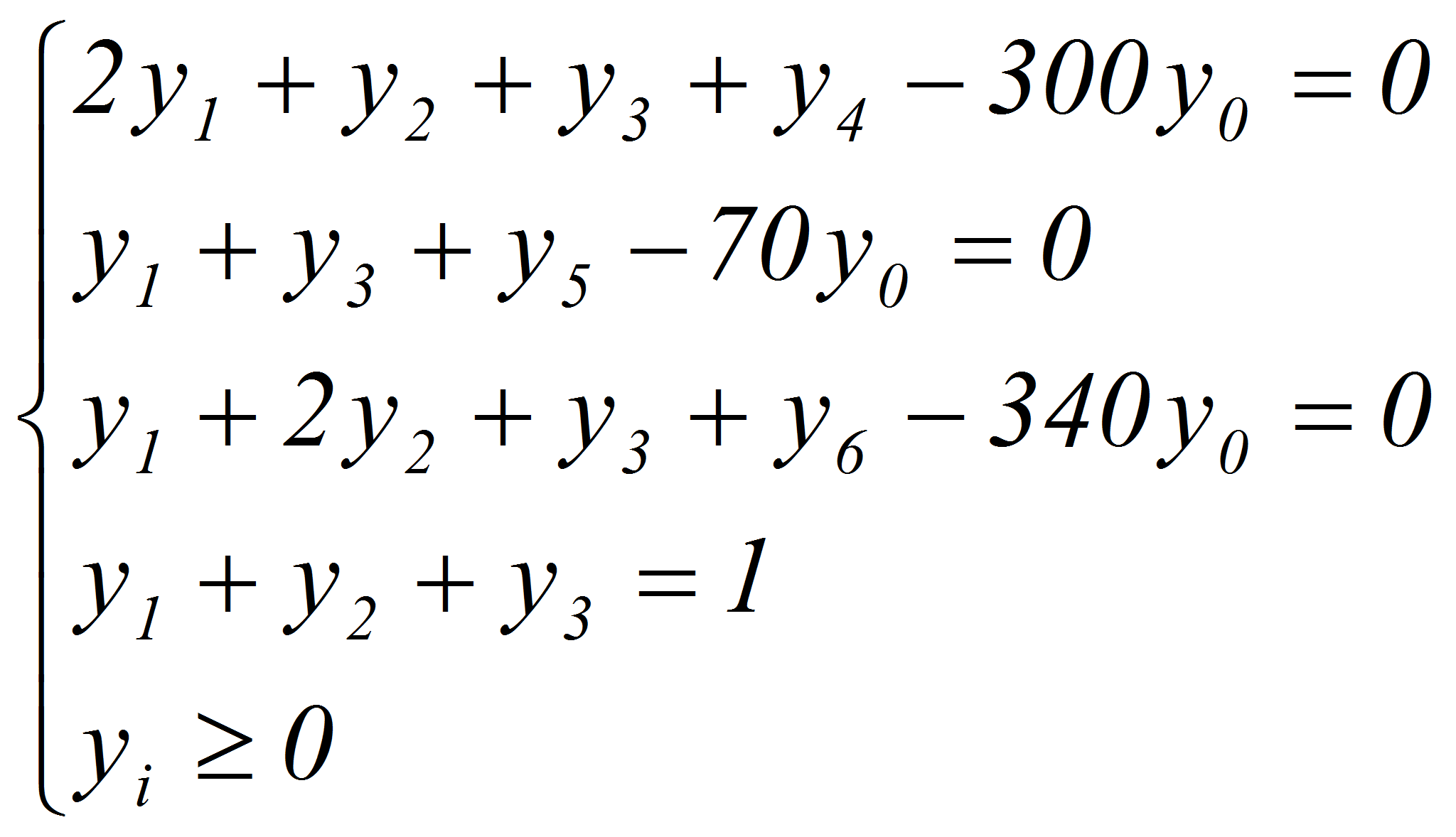В настоящее время широко разработаны вопросы традиционной оптимизации систем с детерминированными параметрами [1,2]. С математической точки зрения такая оптимизация есть отыскание экстремумов функции, параметры которых детерминированные (полностью определенные) величины. Однако на практике чаще встречаются системы с недетерминированными (не полностью определенными) параметрами. Такая оптимизация значит сложнее традиционной [1,2], так как для нее дополнительно необходимы обобщение понятия экстремума функции, выяснение условий существования экстремума недетерминированной функции и разработка специальных методов поиска экстремумов таких функций. В начале 1990-х годов в работах первого из авторов [3] был предложен некоторый общий подход к проблеме и на его основе дано решение недетерминированных версий ряда популярных задач оптимизации (линейное программирование, булево линейное программирование, транспортная задача, выпуклое нелинейное программирование, антагонистичная игра). В настоящей работе дано решение, на той же основе, недетерминированной версии еще одной прикладной задачи оптимизации задачи дробно-линейного программирования.
Общая задача дробно-линейного программирования в детерминированной постановке состоит в нахождении максимального значения дробно-линейной функции
где
![]() -
некоторые постоянные числа. Также предполагается, что знаменатель
функции
-
некоторые постоянные числа. Также предполагается, что знаменатель
функции
![]() в области неотрицательных решений системы линейных уравнений (2).
Решение этой задачи имеет своей целью минимизировать себестоимость
выпускаемых изделий.
в области неотрицательных решений системы линейных уравнений (2).
Решение этой задачи имеет своей целью минимизировать себестоимость
выпускаемых изделий.
Рассмотрим недетерминированный (интервальный) вариант задачи (1),(2), состоящий в определении максимального значения интервального обобщения функции (1)
при детерминированных условиях
![]()
![]()
![]()
![]() (4)
(4)
где
![]() и
и
![]() - интервалы вида
- интервалы вида
![]() ,
,
![]() ,
в которых
,
в которых
![]() ,
,
![]() - минимальные значения интервальных коэффициентов (нижние границы
интервалов), а
- минимальные значения интервальных коэффициентов (нижние границы
интервалов), а
![]() ,
,
![]() -
максимальные значения интервальных коэффициентов (верхние границы
интервалов),
-
максимальные значения интервальных коэффициентов (верхние границы
интервалов),
![]() -
некоторые постоянные числа,
-
некоторые постоянные числа,
![]() .
.
Будем решать поставленную интервальную задачу
методом детерминизации, т.е. сведением к двум аналогичным
детерминированным задачам. Так как целевая функция является
нелинейной и представляет собой отношение двух линейных функций, то
нижняя граничная задача задачи (3), (4) может быть получена при
замене всех интервальных коэффициентов числителя целевой функции (1)
их нижними границами, а всех интервальных коэффициентов знаменателя
целевой функции их верхними границами. Верхняя граничная задача
задачи (3), (4) может быть получена при замене всех интервальных
коэффициентов числителя целевой функции их верхними границами, а всех
интервальных коэффициентов знаменателя целевой функции их нижними
границами. В результате необходимых действий получим два решения двух
введенных детерминированных задач. Решение нижней граничной задачи
дает максимальное значение
![]() ее
целевой функции
ее
целевой функции
![]() ,
являющееся нижней границей интервала-решения исходной задачи (3),
(4), решение верхней граничной задачи дает максимальное значение
,
являющееся нижней границей интервала-решения исходной задачи (3),
(4), решение верхней граничной задачи дает максимальное значение
![]() ее
целевой функции
ее
целевой функции
![]() ,
являющееся верхней границей интервала-решения исходной задачи (3),
(4). Т.о. решение исходной задачи, т.е. максимум интервальной
целевой функции
,
являющееся верхней границей интервала-решения исходной задачи (3),
(4). Т.о. решение исходной задачи, т.е. максимум интервальной
целевой функции
![]() будет достигаться в некоторой точке
будет достигаться в некоторой точке
![]() ,
а значение этого максимума целевой функции при заданных
ограничениях будет
,
а значение этого максимума целевой функции при заданных
ограничениях будет
![]() .
.
Итак, нам необходимо решить две граничные детерминированные оптимизационные задачи – нижнюю граничную и верхнюю граничную.
Задача 1(нижняя граничная задача): Найти максимум функции
Сформулированная задача может быть сведена к задаче линейного программирования. Для этого обозначим
Используя введенные переменные, сведем задачу 1 к следующей задаче: найти максимум функции
при условиях
Задача (9)-(11) является задачей линейного программирования.
Следовательно, ее решение можно найти соответствующими известными
методами [1,2]. Зная оптимальный план решения этой задачи на основе
соотношении (8) получаем оптимальный план решения задачи 1.
Максимальное значение
![]() целевой функции
целевой функции
![]() задачи
1- нижней граничной задачи исходной задачи (3),(4) - является нижней
границей интервального максимального значения функции (3).
задачи
1- нижней граничной задачи исходной задачи (3),(4) - является нижней
границей интервального максимального значения функции (3).
Задача 2 (верхняя граничная задача): Найти максимум функции
Сформулированная задача, как и задача 1, может быть сведена к задаче линейного программирования. Для этого обозначим
и введем новые переменные
![]()
![]() .
(15)
.
(15)
Используя введенные переменные, сведем задачу 2 к следующей: найти максимум функции
при условиях
Задачу (16)-(18), как и задачу (9)-(11), решаем известными методами решения задач линейного программирования.
В результате получаем максимальное значение
![]() целевой функции
целевой функции
![]() задачи 2 верхней граничной задачи исходной задачи (3), (4). Это
значение является верхней границей интервального максимального
значения
задачи 2 верхней граничной задачи исходной задачи (3), (4). Это
значение является верхней границей интервального максимального
значения
![]() функции (3).
функции (3).
Так как система ограничений (4) интервальной задачи (3),(4) была
детерминированной, то системы ограничений (6) и (13) задач 1 и 2
совпадают. При этом, оказалось, что точки максимума целевых функции в
задачах 1 и 2 тоже совпадают. В результате решений задач 1 и 2
получаются граничные значения интервального максимума целевой функции
![]() интервальной
задачи (3),(4). Т.о. интервальный максимум значений целевой функции
интервальной
задачи (3),(4). Т.о. интервальный максимум значений целевой функции
![]() (3) при заданных ограничениях (4) получается в виде
(3) при заданных ограничениях (4) получается в виде
![]() ,
где
,
где
![]() - решение задачи 1,
- решение задачи 1,
![]() - решение задачи 2.
- решение задачи 2.
Пример: Найти максимальное значение функции
![]() (19)
(19)
Переменные
![]() могут принимать только лишь неотрицательные значения.
могут принимать только лишь неотрицательные значения.
Таким образом, математическая постановка задачи состоит в определении неотрицательного решения системы линейных неравенств (4), при котором достигается максимум функции F.
Решим нижнюю граничную задачу. Рассмотрим значение целевой функции
при нижних границах интервалов коэффициентов
![]() и верхних границах коэффициентов
и верхних границах коэффициентов
![]() .
.
От неравенств перейдем к равенствам, введем дополнительные переменные
Введем новую переменную
![]() ,
перейдем к новым переменным
,
перейдем к новым переменным
![]() .
.
Запишем систему ограничений в новых переменных
Решив задачу симплекс-методом, получим следующие значения переменных
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Сделав возврат к исходным переменным, получим следующее решение в
виде точки
.
Сделав возврат к исходным переменным, получим следующее решение в
виде точки
![]() ,
,
![]() ,
,
![]() .
Значение целевой функции
.
Значение целевой функции
![]() .
.
Решим верхнюю граничную задачу. Рассмотрим значение целевой функции
при верхних границах интервалов коэффициентов
![]() и нижних границах интервалов коэффициентов
и нижних границах интервалов коэффициентов
![]() .
.
От неравенств перейдем к равенствам, введем дополнительные переменные
Введем новую переменную
![]() ,
перейдем к новым переменным
,
перейдем к новым переменным
![]()
Запишем систему ограничений в новых переменных
Решив задачу симплекс-методом, получим следующие значения переменных
![]() ,
,
![]() ,
,
![]()
![]() .
Сделав возврат к исходным переменным, получим следующее решение в
виде точки
.
Сделав возврат к исходным переменным, получим следующее решение в
виде точки
![]() ,
,
![]() ,
,
![]() .
Соответствующее максимальное значение целевой функции
.
Соответствующее максимальное значение целевой функции
![]() .
.
Искомый максимум
![]() интервальной
целевой функции
интервальной
целевой функции
![]() (3) при заданных ограничениях (4) находится в общей точке (70;0;0)
решения двух граничных задач, а сам максимум целевой функции получаем
соединением двух максимальных значений целевой функции двух
граничных задач
(3) при заданных ограничениях (4) находится в общей точке (70;0;0)
решения двух граничных задач, а сам максимум целевой функции получаем
соединением двух максимальных значений целевой функции двух
граничных задач
![]() .
.
-
- Литература:
Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986. 317 с.
Волошин Г.Я. Методы оптимизации в экономике. – М.: Дело и сервис, 2004. 320с.
Левин В.И. Интервальные методы оптимизации систем в условиях неопределенности. – Пенза: Изд-во ПТИ, 1999. 101с.