Эпитропные жидкие кристаллы (ЭЖК) - это жидкокристаллическое состояние, которое образуется немезогенными жидкостями и возникает у поверхности лиофильной твердой подложки [1]. Организация ЭЖК слоев (приповерхностных ориентационно упорядоченных слоев жидкости) связана с дальнодействующими поверхностными силами, влияние которых распространяется на молекулы жидкости не более, чем на несколько молекулярных слоев [2]. Однако, на металлической подложке индивидуальные предельные углеводороды, смазочные жидкости на их основе (минеральные масла SAE 15W40, ВР180) образуют ЭЖК слои при Т~295 К толщиной ~1÷5 мкм. Кроме того, установлено, что степень молекулярной упорядоченности в ЭЖК слоях (в частности, в ЭЖК слоях н-алканов) убывает по мере удаления от подложки [3,4]. Это свидетельствует о несовершенстве представленной в [3] упрощенной реологической модели течения прослойки с квазижидкокристаллическими слоями.
В связи с этим предлагается новый взгляд на организацию ЭЖК. А именно, ЭЖК слои представляют собой объект с фрактальной структурой – фрактальный кластер, образованный молекулами жидкости на металлической подложке.
Задачей исследования стало изучение структуры ЭЖК слоев н-тетрадекана и выявление ее фрактальной природы.
Широко известно определение фрактала, данное Мандельбротом: фрактал представляет самоподобное (в смысле изменения масштаба) множество, размерность которого отличается от топологической [5,6]. Фрактальный кластер (или фрактальный агрегат) является одним из объектов с фрактальной структурой. Такая система имеет рыхлую и ветвистую структуру и образуется в большом наборе физических процессов, сопровождающихся ассоциацией твердых частиц близких размеров. Одним из свойств фрактального кластера является то, что по мере его роста падает средняя плотность вещества в объеме, занимаемом кластером [5].
Физические системы обладают характерным минимальным линейным размером, таким как радиус R0 атома или молекулы. Известная форма для соотношения между числом частиц и размером кластера, который оценивается по радиусу R наименьшей сферы, содержащей кластер внутри себя, имеет вид:
где Df - размерность кластера, не зависящая от его формы. Фрактальная размерность кластера служит количественной характеристикой того, как кластер заполняет занимаемое им пространство [6,7].
В [8] была получена фрактальная формула зависимости вязкости от градиента скорости &#;:
η= η0(1+k&#;-α), (2)
где k - константа, &#;-- градиент скорости, α=p(Df+1) (Df - фрактальная размерность площади агрегата; p - величина, характеризующая потенциал взаимодействия коллоидных частиц и кинетику формирования фрактального агрегата).
Объектом исследования был представитель н-алканов - тетрадекан
![]() (Тпл=278,8 К). Индивидуальные жидкости удобны для
исследования ввиду известного строения их молекул. Изучались
температурные зависимости коэффициента вязкости тетрадекана в его
микронных прослойках, в которых наличие ЭЖК существенно и может
повлиять на этот коэффициент. При этом для измерений вязкости тонких
прослоек жидкостей использовался ротационный вискозиметр [3].
(Тпл=278,8 К). Индивидуальные жидкости удобны для
исследования ввиду известного строения их молекул. Изучались
температурные зависимости коэффициента вязкости тетрадекана в его
микронных прослойках, в которых наличие ЭЖК существенно и может
повлиять на этот коэффициент. При этом для измерений вязкости тонких
прослоек жидкостей использовался ротационный вискозиметр [3].
Измеряемая «эффективная» вязкость &#;eff микронных прослоек тетрадекана сравнивалась с его вязкостью &#;o в «объеме», определяемой капиллярными (&#; ~ 1 мм) вискозиметрами. Экспериментальные зависимости коэффициента относительной вязкости тетрадекана (&#;отн&#;=&#;eff/&#;o) от скорости сдвиговой деформации в его прослойке (толщиной D = 1,5 мкм) ротационной пары вискозиметра для разных температур представлены на рис. 1. Аналогичные зависимости были получены для прослоек толщиной D = 4 мкм. Из рис. 1 следует, что есть некоторый диапазон скоростей деформации γ, в котором эффективные вязкости тетрадекана, измеренные при разных температурах, существенно различаются, причем вязкость увеличивается с понижением температуры. Повышенная, по сравнению с «объемом», вязкость микронной прослойки, как и ранее связана с наличием ЭЖК слоев [3,4]. С увеличением γ, эффективная вязкость жидкостей уменьшается и становится равной «объемной» вязкости жидкости (&#;отн → 1), т. е. вязкости изотропной жидкости.
На рис. 2 приведен график температурной зависимости коэффициента вязкости ms тетрадекана при зазоре D=1,5 мкм, полученный экстраполяцией экспериментальных значений эффективной вязкости в область малых &#;. Из графика видно, что коэффициент вязкости ЭЖК слоя тетрадекана &#;&#;s отличен от вязкости в «объеме» &#;0 и имеет другую температурную зависимость.
Р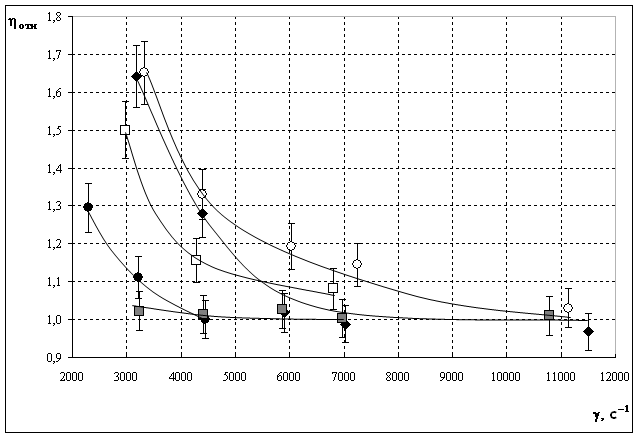
ис.
1. Экспериментальные зависимости относительной вязкости тетрадекана
от скорости сдвиговой деформации, зазор ротационной пары D=1,5
мкм, при температурах Т:○– 285,5 К, ♦–288,8
К, □–293,8 К, ● –297,3 К,
![]() -
300,8 К.
-
300,8 К.
 Рис.
2. Температурные зависимости коэффициента
вязкости &#;s
(&#;) и
коэффициента вязкости «в объеме» &#;0
(&#;)
тетрадекана.
Рис.
2. Температурные зависимости коэффициента
вязкости &#;s
(&#;) и
коэффициента вязкости «в объеме» &#;0
(&#;)
тетрадекана.
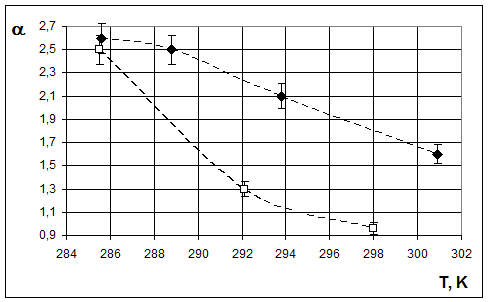
На рис. 3 и 4 представлены зависимости ln(&#;отн-1) от lnγ для прослоек тетрадекана, содержащих ЭЖК слои (для построения этих зависимостей использовался интервал скоростей сдвиговой деформации, в котором &#;отн>1). В соответствии с формулой (2) экспериментальные точки аппроксимировались прямыми линиями. В табл. 1 приведены значения коэффициентов lnk и α. На рис. 5. приведена зависимость коэффициента α от температуры для прослоек тетрадекана толщиной 1,5 и 4 мкм. Из рисунка видно, что эти коэффициенты уменьшаются при увеличении температуры и толщины прослойки. От температуры зависят и величина p, и величина Df. По нашему мнению, зависимость коэффициента α от толщины прослойки тетрадекана свидетельствует о различных фрактальных размерностях микронных прослоек тетрадекана, обусловленных разной степенью перекрытия ЭЖК слоев в таких тонких прослойках.
Убывание степени молекулярной упорядоченности в ЭЖК слоях (в частности, в ЭЖК слоях н-алканов) по мере удаления от подложки, вообще говоря, приводит к более рыхлой упаковке мономеров в них и снижению плотности по мере удаления от подложки.
Р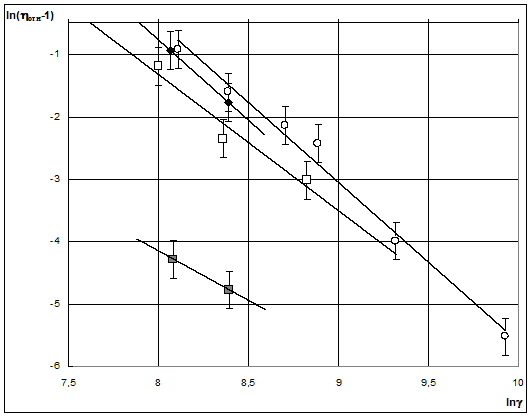
ис.
3. Зависимость ln(&#;отн-1)
от ln(γ) для прослойки тетрадекана,
толщина прослойки D=1,5 мкм, при
температуре Т: :○– 285,5 К, ♦–288,8 К,
□–293,8 К,
![]() -
300,8 К.
-
300,8 К.
-
- Р
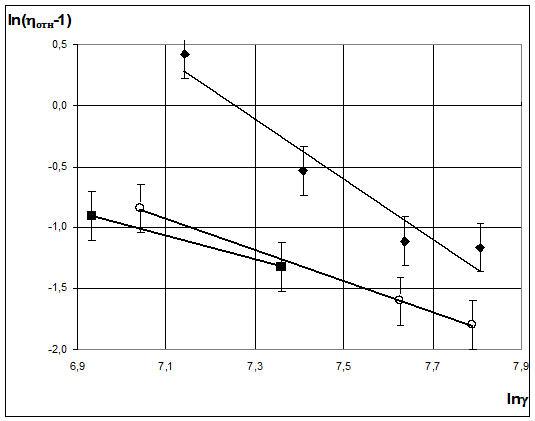
ис. 4. Зависимость ln(&#;отн-1) от ln(γ) для прослойки тетрадекана, толщина прослойки D=4 мкм, при температуре Т: &#;- 285,5 К, ○-292,1 К С, ■ -298 К.
- Р
Таблица 1
Постоянные lnk и α для тетрадекана
|
D, мкм |
Т,К |
lnk |
α |
|
|
285,6 |
~20,5 |
2,6 |
|
1,5 |
288,8 |
~20 |
2,5 |
|
|
293,8 |
~16 |
2,1 |
|
|
300,9 |
~9 |
1,6 |
|
|
285,5 |
~18 |
2,5 |
|
4 |
292,1 |
~7,5 |
1,2 |
|
|
298 |
~6 |
0,96 |
Рис. 5. Зависимость коэффициента α от температуры для прослоек тетрадекана толщиной: &#;- 1,5 мкм, &#;- 4 мкм.
Все вышесказанное позволяет нам сделать вывод о том, что ЭЖК слои представляют собой объект с фрактальной структурой – трехмерный фрактальный кластер, растущий на твердой подложке. Очевидно, что необходимо дальнейшее изучение рассматриваемого вопроса, что и станет задачей наших последующих исследований.
Выводы
В связи с проявлением ЭЖК слоев в микронных прослойках н-тетрадекана, вязкость последних отлична от вязкости в «объеме» и имеет иную температурную зависимость.
ЭЖК слои представляют собой объект с фрактальной структурой – фрактальный кластер.
Явление убывания степени молекулярной упорядоченности в ЭЖК слоях по мере удаления от подложки связано с фрактальной природой ЭЖК.
Литература:
Дерягин Б. В. Открытие СССР «Явление образования гомогенной граничной жидкокристаллической фазы немезогенной жидкости». Диплом №388. / Б. В. Дерягин, Ю. М. Поповский, Б. А. Алтоиз //Открытия и изобретения. – 1991. №12. – С. 1.
Алтоиз Б.А. Модель Изинга эпитропной ЖК фазы / Б.А. Алтоиз, Ю.М.Поповский, Е.С.Ляхова // Колл. ж. – 2000. – Т.62, №3. – С.299-302.
Алтоиз Б.А. Исследование эффективной вязкости тонких прослоек алифатических жидкостей в поле флуктуационных сил, порождаемых твердыми подложками / Б.А. Алтоиз, С.В. Кириян, Е.А. Шатагина // Журнал технической физики. – 2010. – Т.80, № 10. – С. 37-40.
Altoiz B.A. Structural rheological model of two-phase interlayer shear flow / B.A. Altoiz, S.K. Aslanov, S.V. Kiriyan // Zeitschrift für Angewandte Mathematik und Physik. – 2011. – V. 62, № 2. – P. 195–202.
Смирнов Б.М. Физика фрактальных кластеров / Б.М. Смирнов / М.: Наука.–1991. – 136 с.
Шмидт Ф.К. Фрактальный анализ в физико-химии гетерогенных систем и полимеров / Ф.К. Шмидт / Иркутск, ИГУ.– 2001. – 181 с.
Федер Е. Фракталы \Е. Федер\ М.: Мир. – 1991. – 254 с.
Лесин В. И. Фрактальная формула зависимости вязкости неньютоновской жидкости от градиента скорости / В. И. Лесин // Георесурсы. Геоэнергетика. Геополитика. – 2011. – №1(3). oilgasjournal.ru.