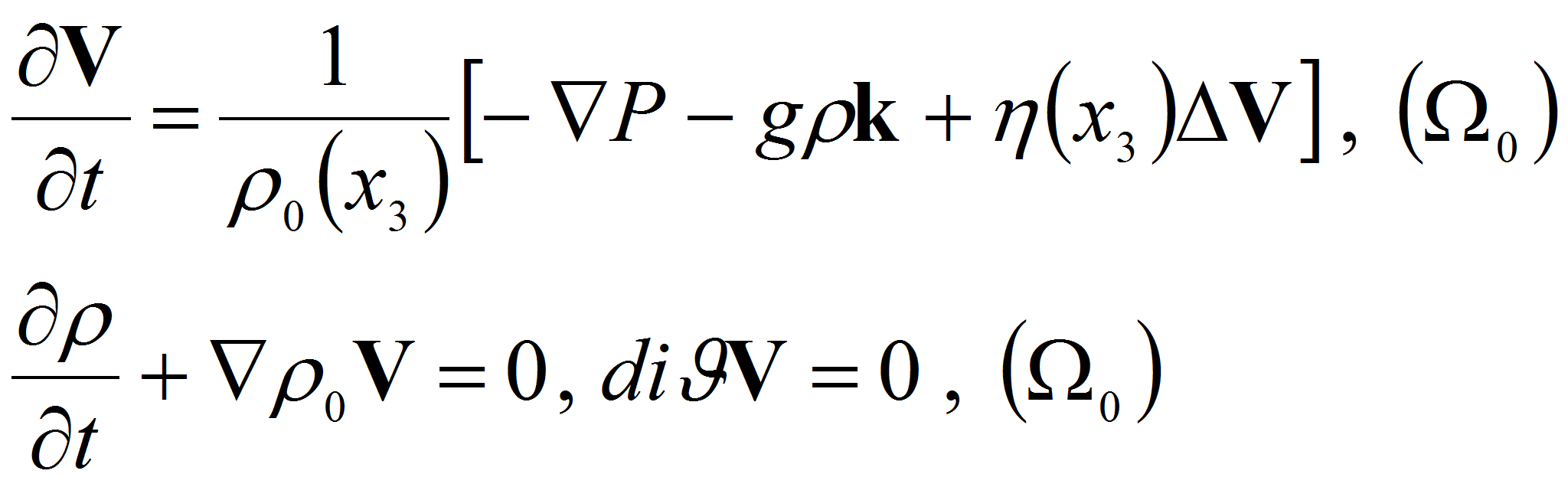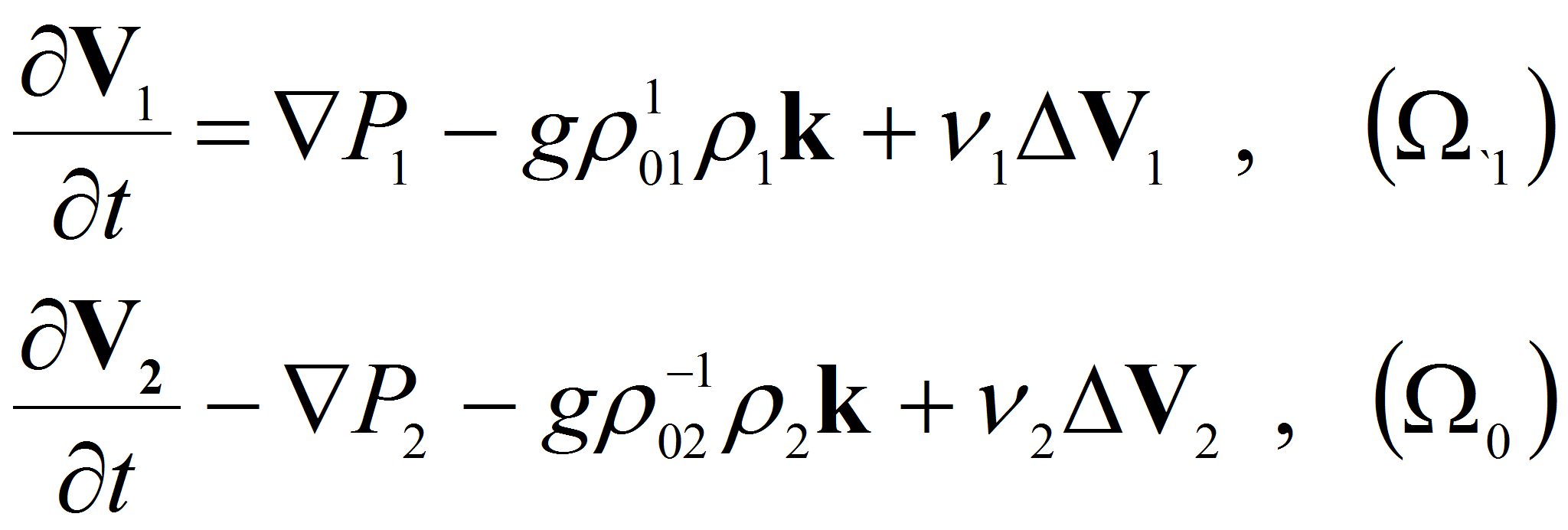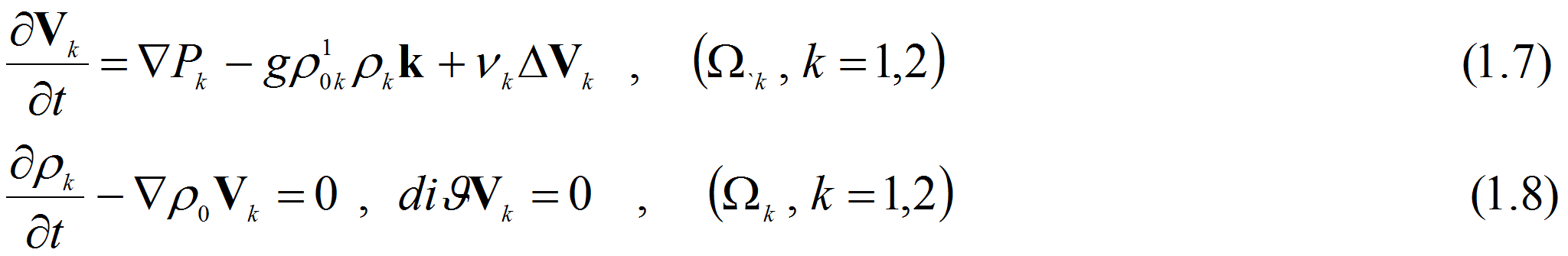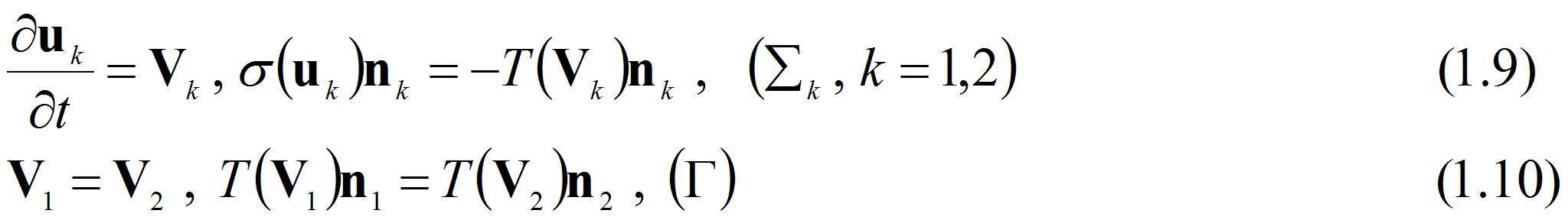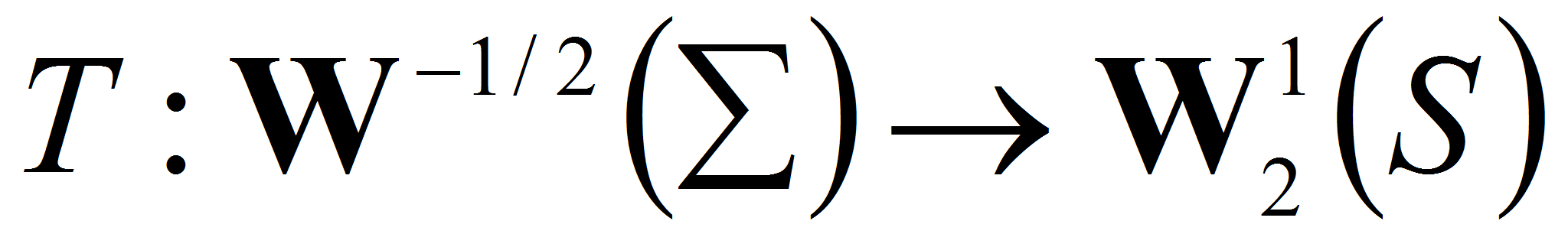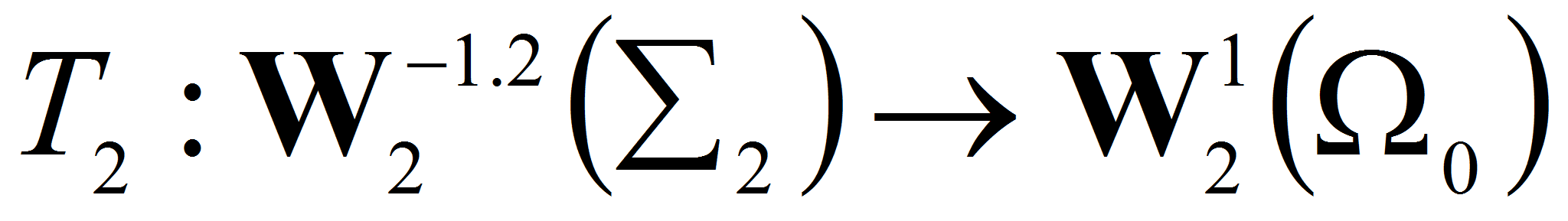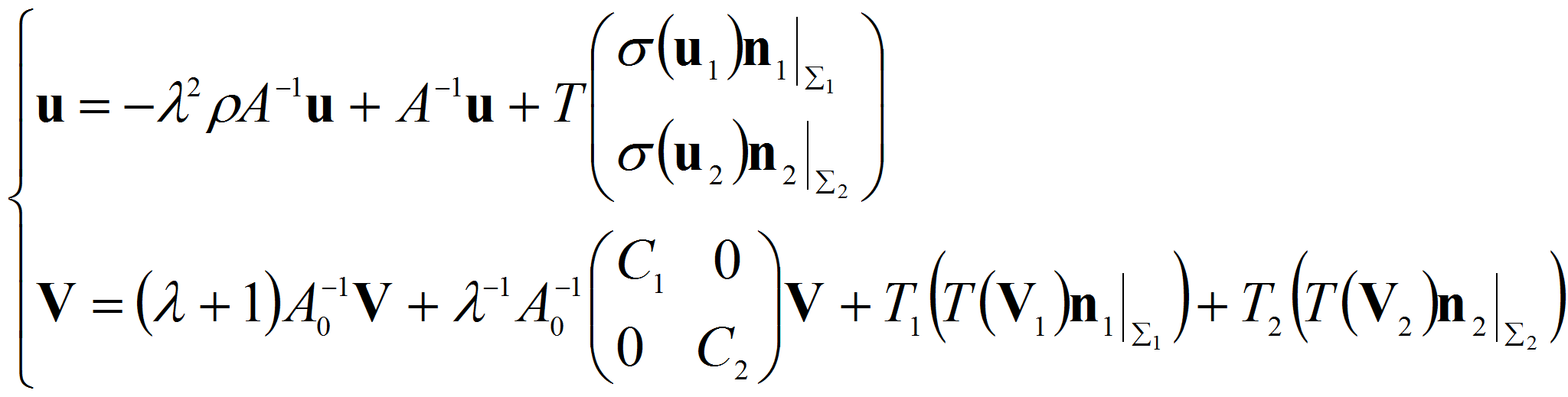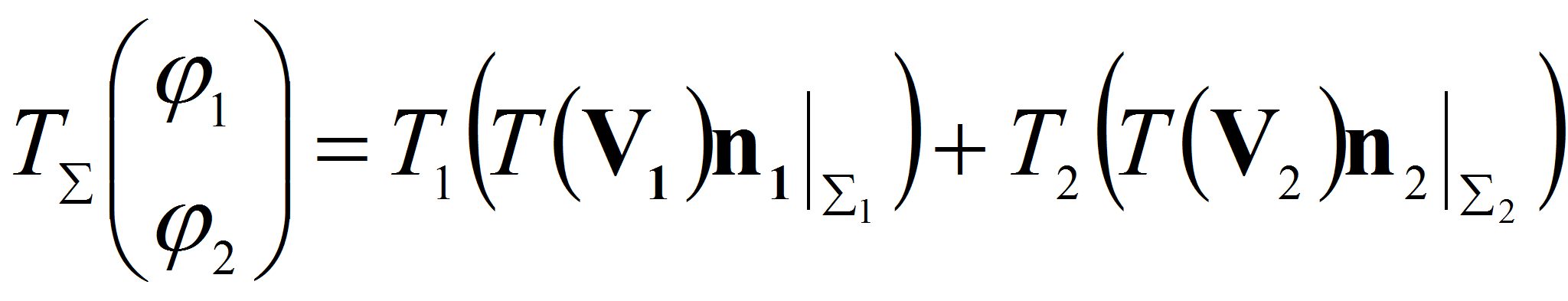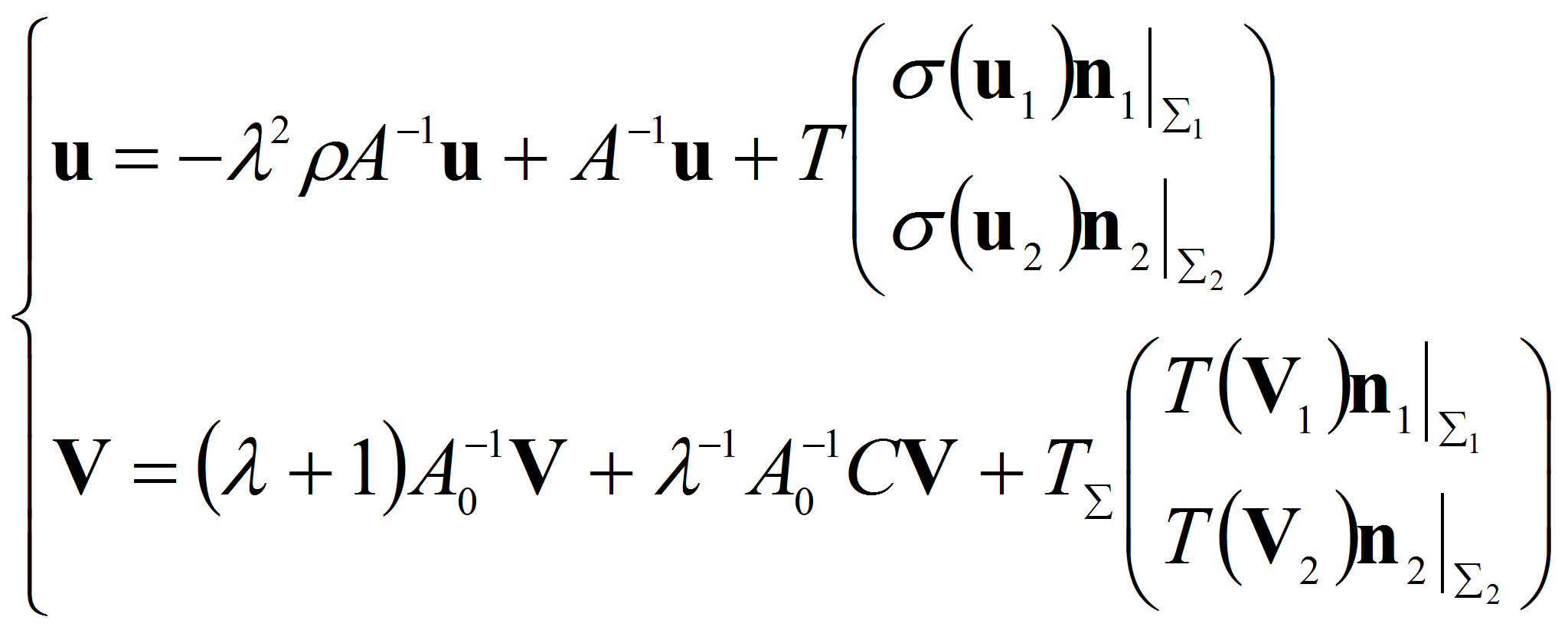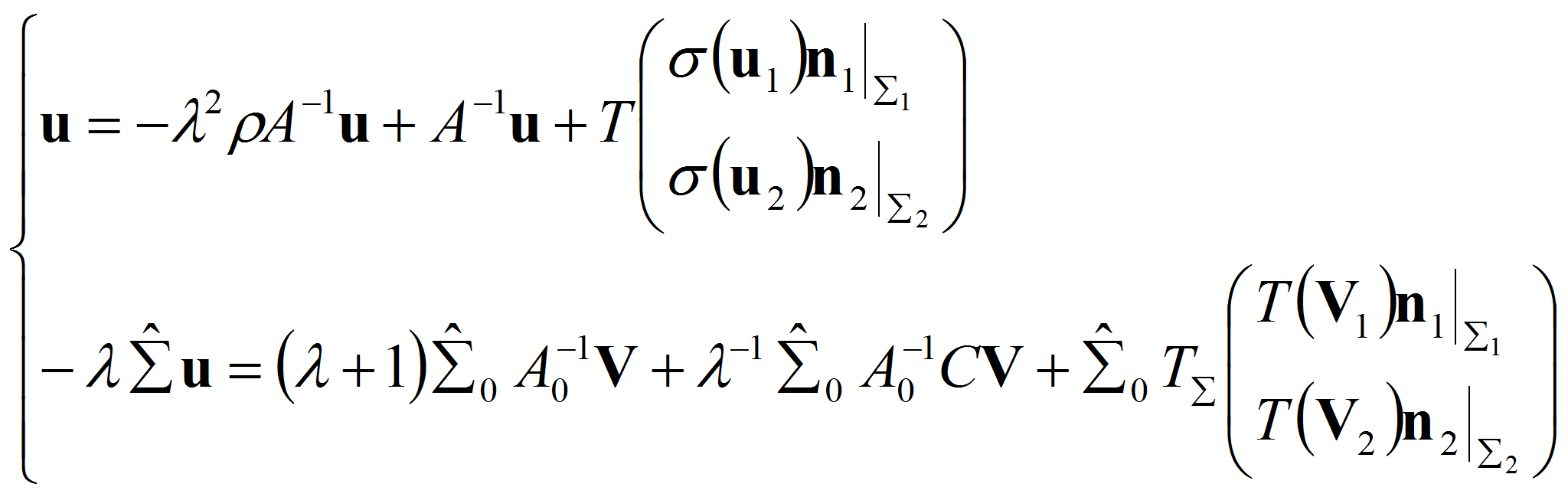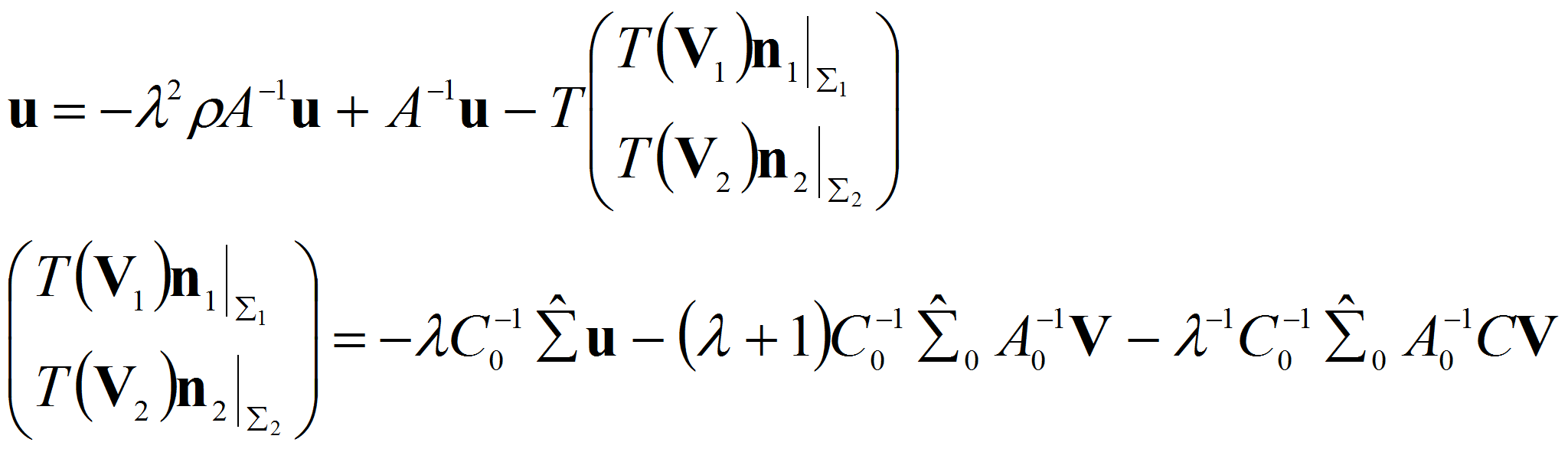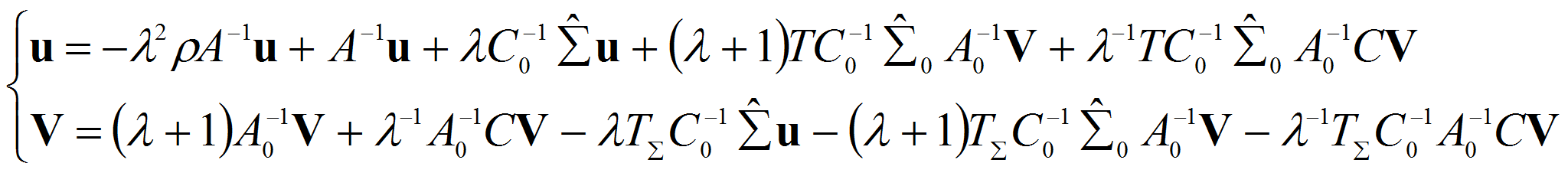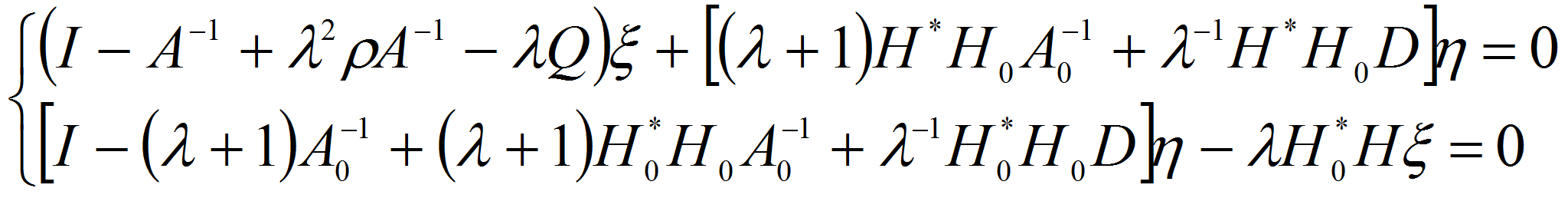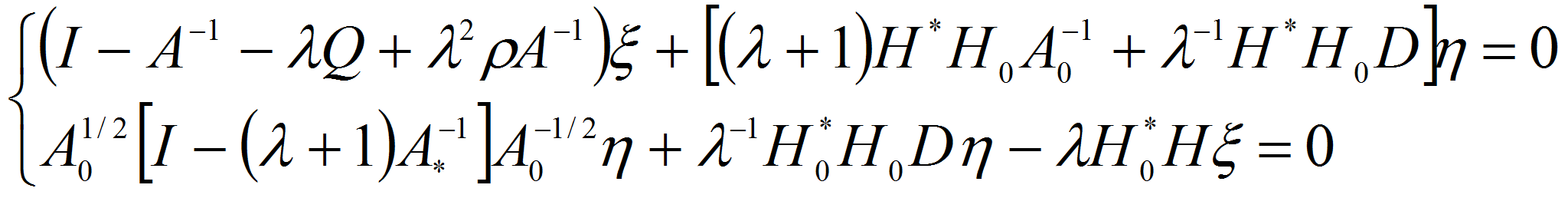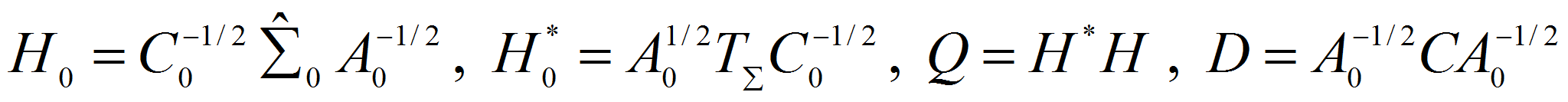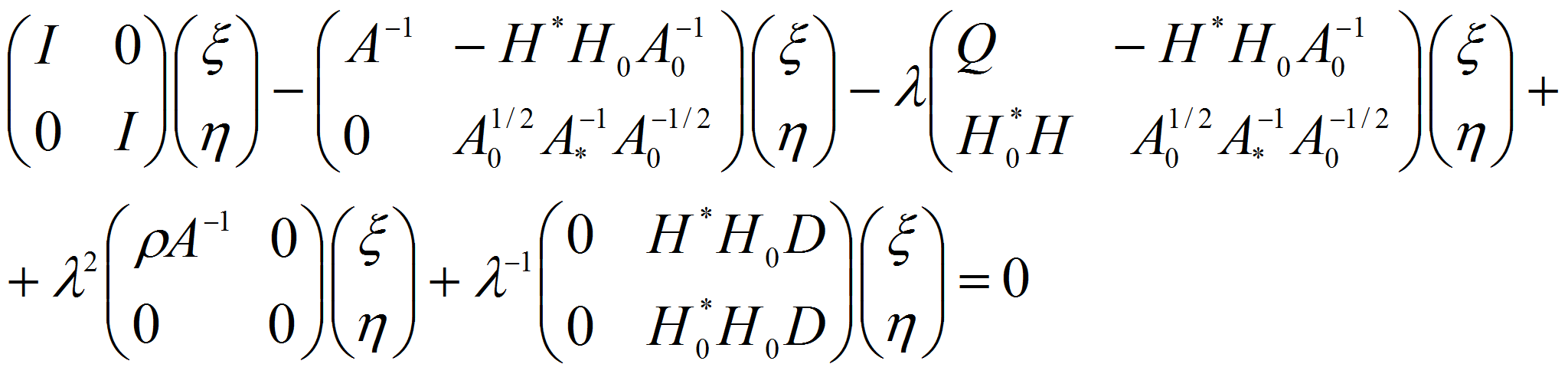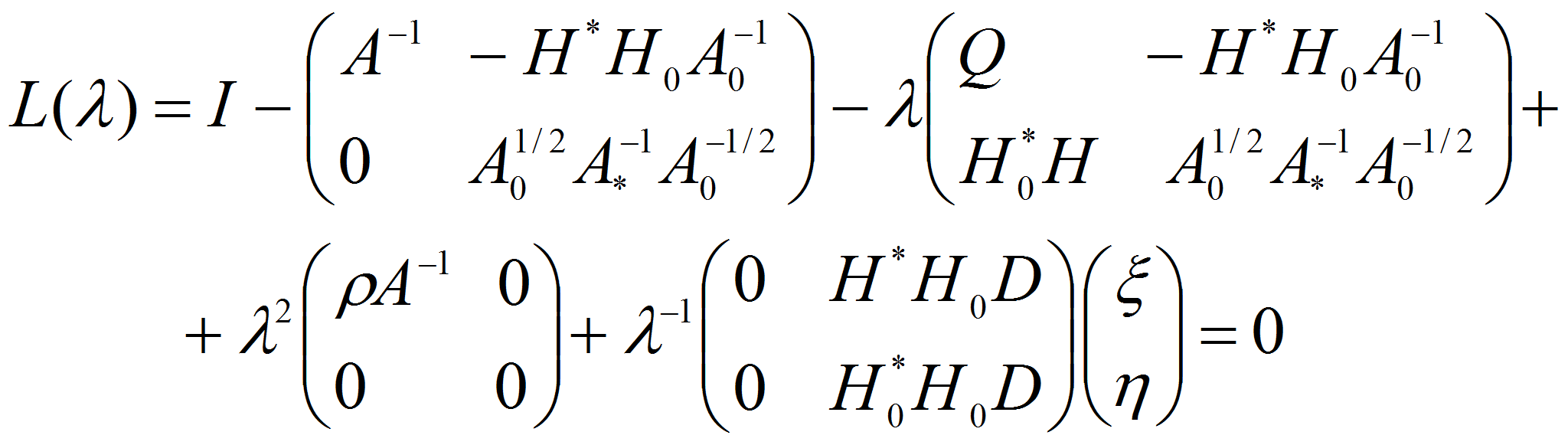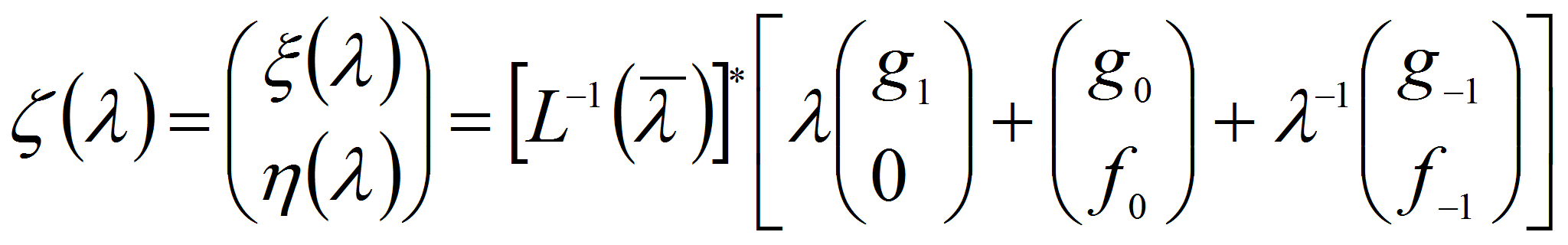Задача о нормальных колебаниях системы вязких стратифицированных жидкостей в упругом сосуде

Изучаются свойства собственных значений и собственных функций в задаче о нормальных колебаниях вязкой несжимаемой стратифицированной жидкости, заполняющей упругий сосуд. Получены утверждения о локализации спектра и доказана терема о полноте собственных функций с конечным дефектом.

Изучение задач о движении жидкости в сосуде относятся к числу классических задач гидромеханики. Движения жидкости и сосуда, зависящие от времени как называются нормальными или свободными.

Задачи о колебаниях вязкой стратифицированной жидкости в неподвижном сосуде рассматривались в . В были исследованы некоторые задачи о колебаниях вязкой несжимаемой однородной жидкости в упругом сосуде, однако условия согласования между жидкостью и упругим сосудом в этой работе носили математической характер.

Настоящая работа посвящена задаче о нормальных колебаниях системы вязких несжимаемых стратифицированных жидкостей в упругом сосуде. При этом условия согласование между упругой стенкой и жидкостью будет выписано, как это принято в линейной теории. Часть результатов данной работы изложена в .

1. Постановка задачи. Рассмотрим ограниченную область и пусть подобласть и , причем границы класса .

Пусть в упругом сосуде занимающем область находится система из двух вязких стратифицированных несжимаемых жидкостей заполняющая область . Границы раздела жидкостей обозначим через . Пусть и части , лежащие соответственно ниже и выше . . 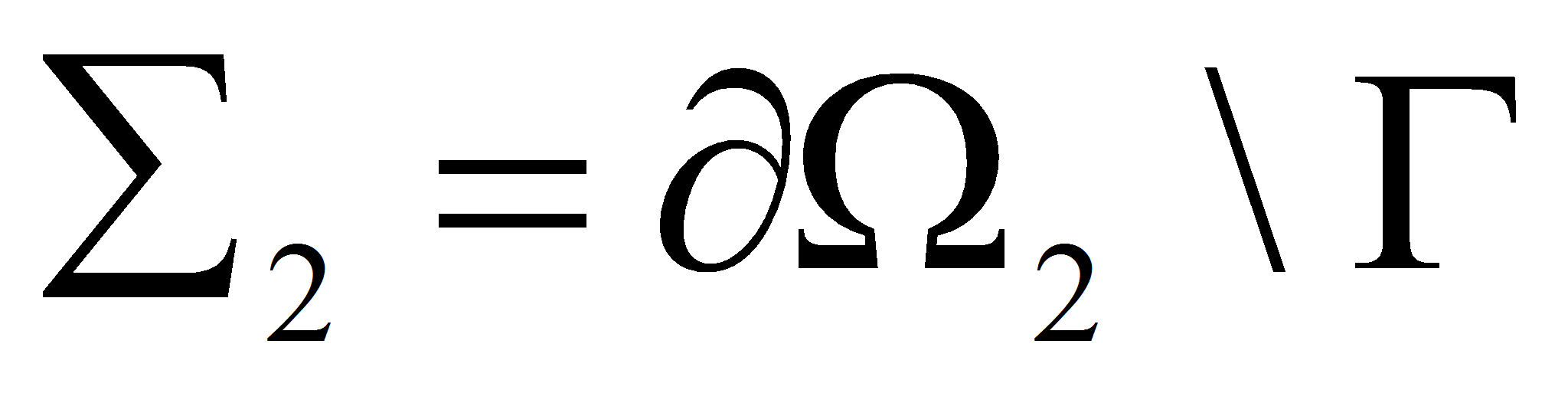Соответствующий участок упругого сосуда обозначим через Напомним, что основным частотным параметром, характеризующий распространение и типы волн в стратифицированной жидкости, является так называемая частота Вяйсяля – Брента которая определяется соотношением

(1.1)

где и соответственно стационарное распределение плотности и его производная, а ускорение свободного падения. Будем считать, что на стратифицированную жидкость действует гравитационное поле с ускорением оси декартовой системы координат . Рассматривается случай устойчивой стратификации жидкости:

(1.2)

где считается непрерывной функцией Тогда в приближении Буссинеска линеаризованные уравнения движения стратифицированной вязкой жидкости в объеме примут вид

(1.3)

где динамическая вязкость, отклонение плотности от положения равновесия скорость частицы жидкости. Чтобы упростить первое уравнение из (1.3) в области заменим его приближенными уравнениями в областях и

(1.4)

где константы, усредняющие в областях и значений усредняют значения отклонения плотности от положения равновесия в областях и . При этом на границе соприкосновения должны, очевидно, выполнятся условия

(на Г) (1.5)

где первое равенство означает непрерывность скорости, а второе – равенство напряжений. Здесь

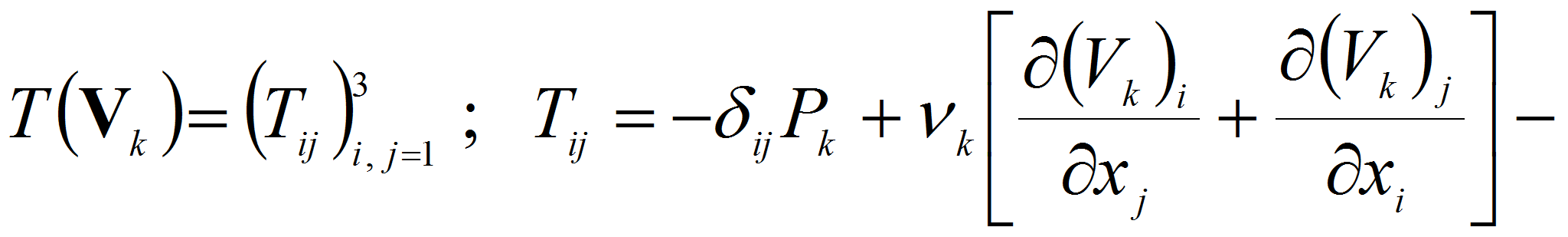тензор Навье – Стокса, соответствующий течению внешняя нормаль на Г к .

Если теперь область заполнена вязкой стратифицированной жидкостью, уравнения движения которой мы описываем приближенной системой (1.4) , (1.5) то уравнения свободных колебаний такой механической системы примут вид:

(1.6)

(1.11)

Здесь вектор смешения, а

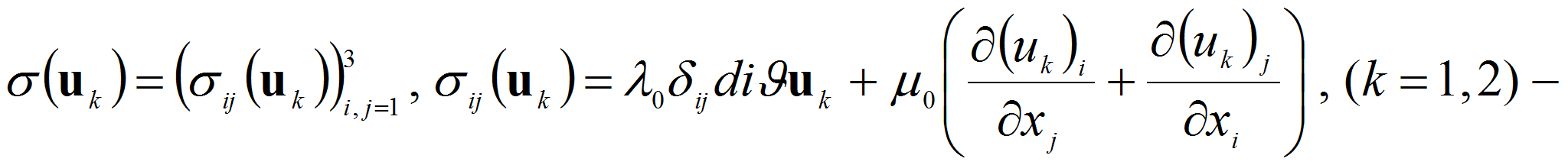тензор напряжений изотропного упругого тела, постоянные Ляме, символ Кронекера, плотность тела, нормаль внешняя к той области, из которой берется нормальная производная. Краевое условие (1.6) означает отсутствие напряжений на Первое равенство (1.9) является условием прилипания вязкой жидкости на стенке а второе равенство напряжений на . (1.11) начальные данные.

Чтобы получить задачу на собственные значения будем искать решения, зависящие от времени как Подставляя решение такого вида в (1.6) – (1.10) и с помощью возникающих равенств

исключая плотности , придем к системе

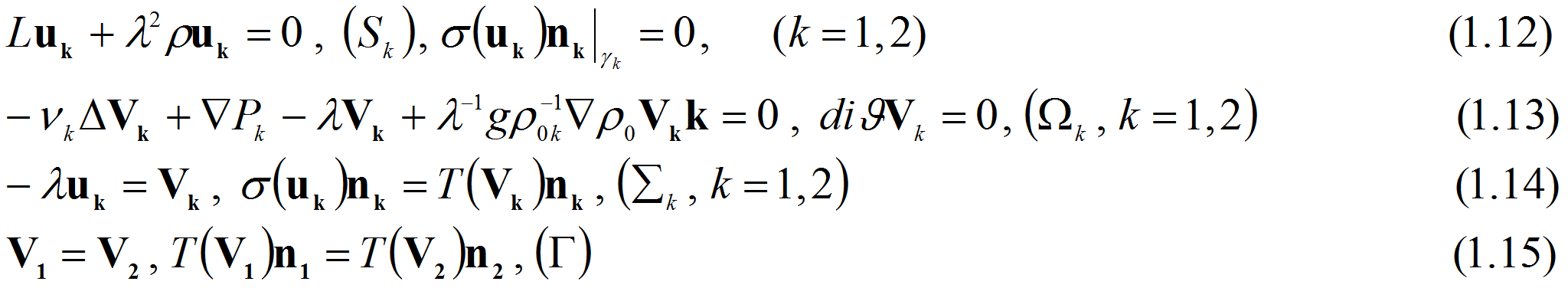Именно эта система является объектом исследования последующих пунктов и цель которую мы ставим, состоит в том чтобы изучить структуру спектра и свойства собственных функций указанной задачи.

2. Переход к операторному уравнению. Положим

и обозначим подпространство в .

Пусть ортопроектор.

Для дальнейшего исследования задачу (1.12) – (1.15) сведем к операторному пучку. С этой целью рассмотрим следующие вспомогательные задачи:

Задача I. По функции найти решение задачи

Задача II. По функции 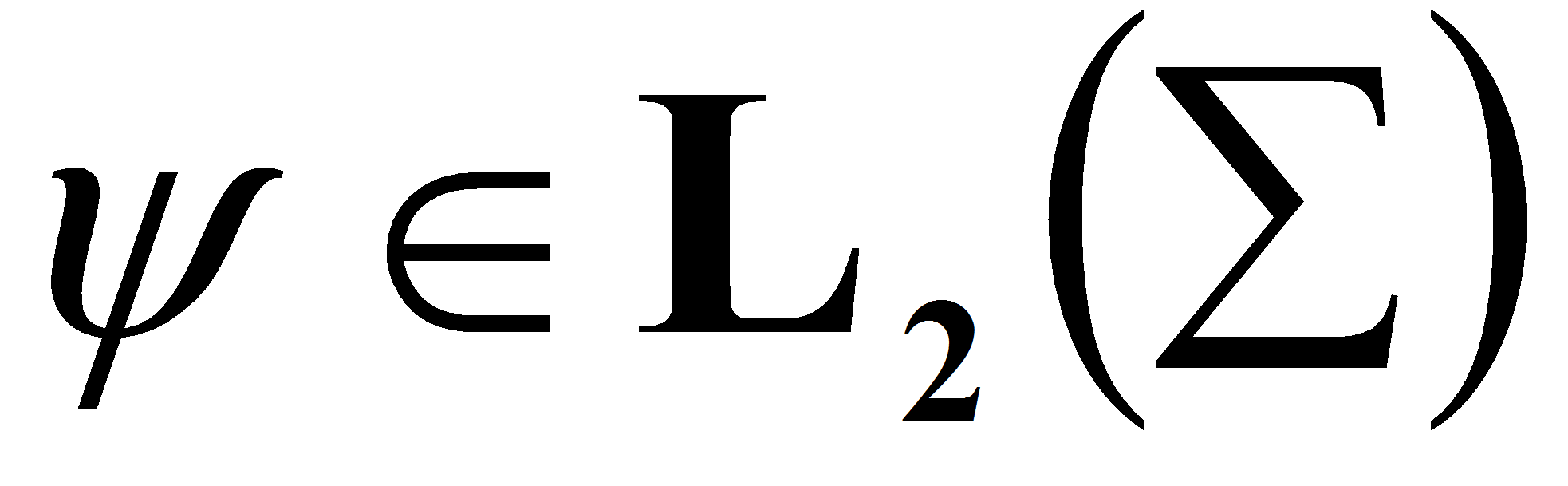найти решение задачи

Задача III. Для функции найти решение задачи

Задача IV. По функции найти решение задачи

Из результатов работ и следует каждой из этих задач отвечает оператор, которой однозначно задает обобщенное решение задачи. Выпишем последовательно обозначения для этих операторов и перечислим их свойства.

I. В задаче I возникает компактный оператор причем

и .

II. В задаче II возникает непрерывный оператор

действующий по правилу .

III. В задаче III возникает компактный, самосопряженный оператор

причем и .

IV. В задаче IV (а) возникает непрерывный оператор

и .

В задаче IV (б) возникает непрерывный оператор

и .

Заметим теперь, что если решение задачи, отвечающее числу , то с помощью введенных операторов задача (1.12-1.15) может быть записана в виде системы:

где

Введем операторы

Тогда последнюю систему можно записать в виде

(2.1)

Учитывая, что в силу (1.14) 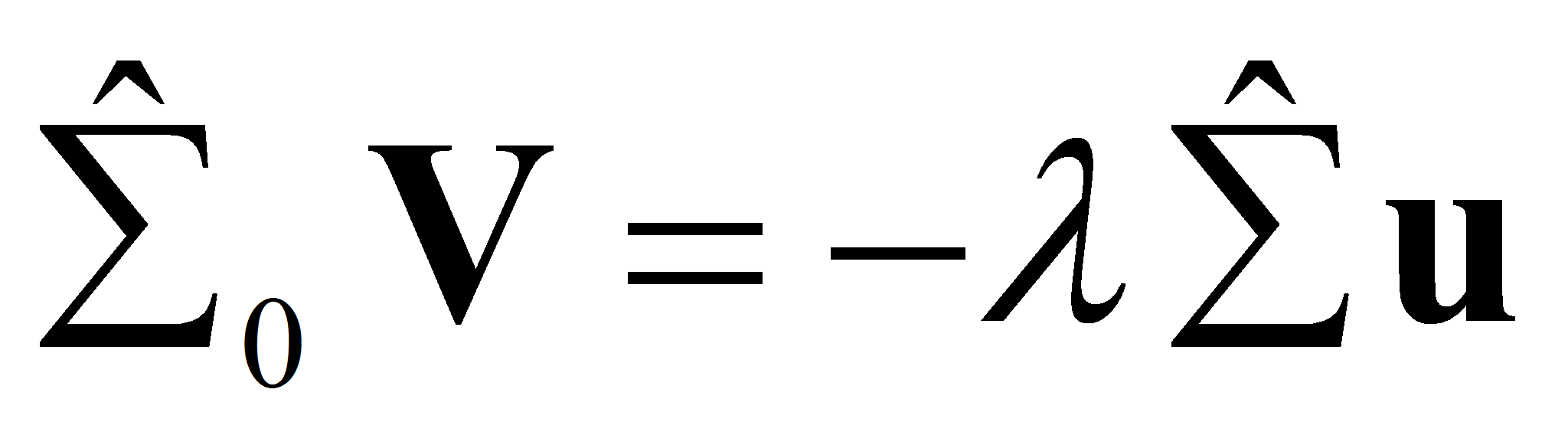и применяя к второму равенству системы (2.1) оператор взятия следа получим

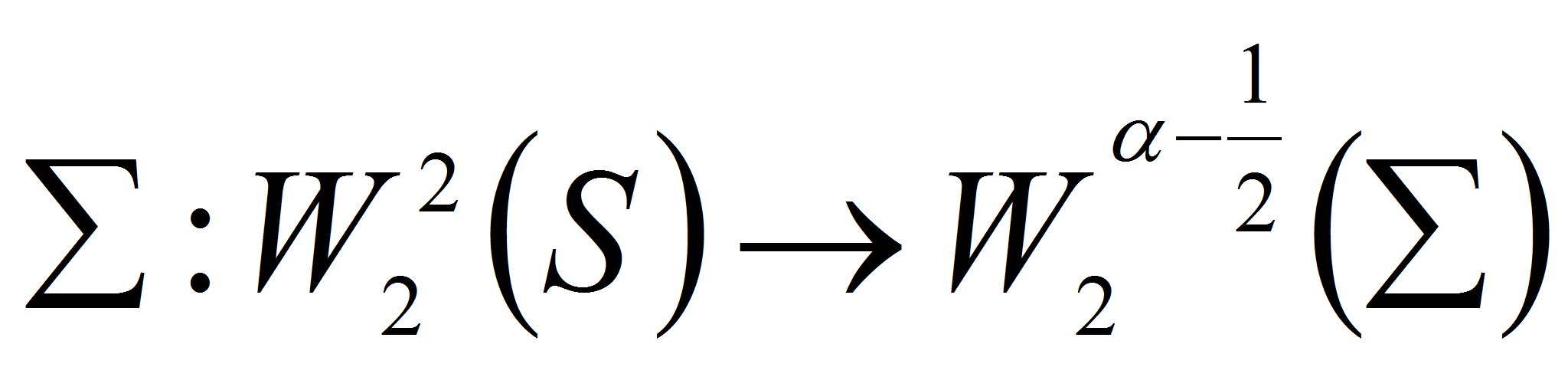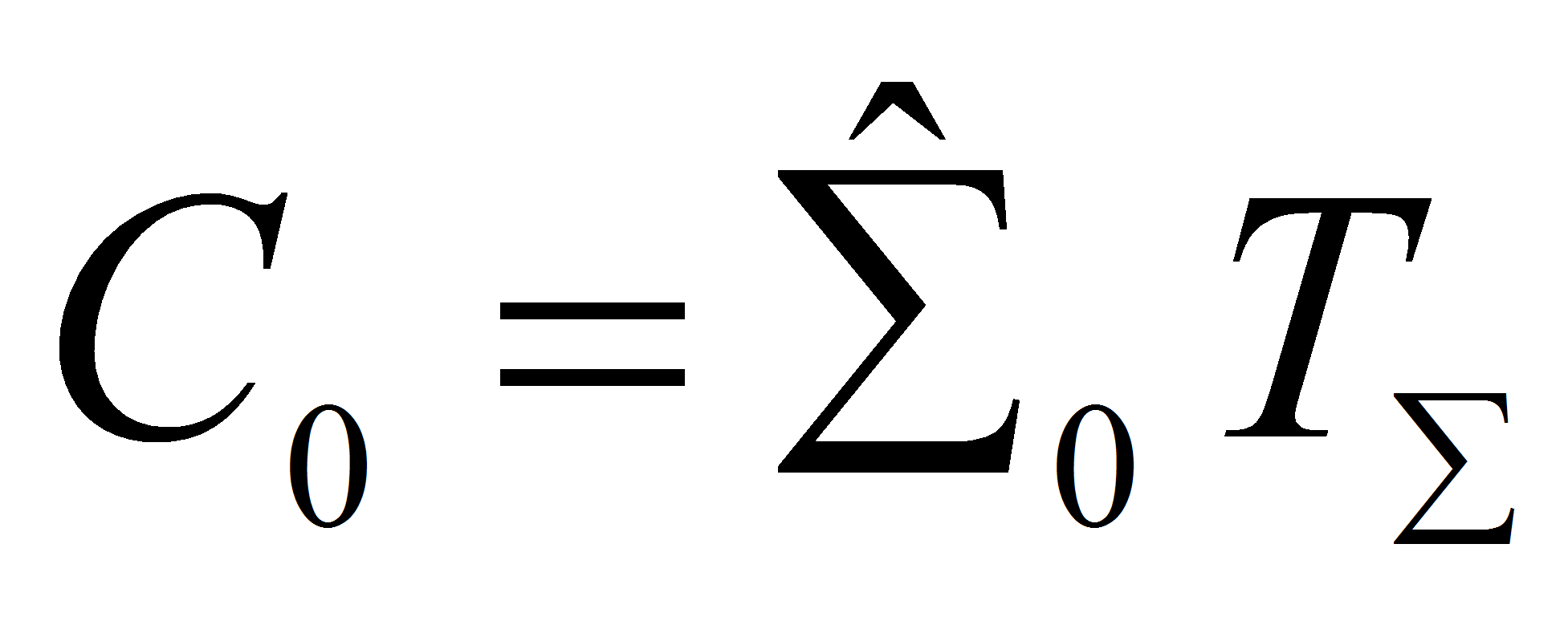где оператор взятия следа Введем обозначение , тогда учитывая получим

Подставляя последнего формулу в первое и второе уравнение системы (2.1) получим

Откуда делая замену после некоторых преобразований придем к системе

или

(2.2)

где

систему (2.2) можно переписать в виде

(2.3)

из (2.3) видно, что исходная задача (1.12-15) свелась к исследованию операторного пучка

(2.4)

3. Структура спектра. Утверждение о полноте. Сначала отметим, что так как то операторы определяемые равенствами положительные в .

Оператор непрерывно обратим.

Его сужение на есть самосопряженный положительный компактный оператор, действующий в Из результатов работы известно, что ограничен и его образ является подпространством в . Также получается, что в и ограничен,

ограничены

ограничены.

Исследование операторного пучка приводит к следующему результату.

Теорема. Спектр пучка (2.4) (и задачи (1.12-15)) состоит из собственных значений (с.з.). конечной кратности, имеющих предельные точки в и на , расположен в правой полуплоскости и симметричен относительно вещественной оси. При этом при больших все с.з. , за исключением конечного числа точек попадают в сколь угодно малые углы примыкающие к мнимой оси и положительной полуоси.

Доказательство. Введем обозначения

где

произвольное достаточно малое число а, выбирается достаточно большим,

где достаточно малое число, - также достаточно мало.

Прежде всего подчеркнем, что говоря о свойствах спектра пучка в этой теореме, мы рассматриваем не как пучок с абстрактными оператора перечисленными выше, а как конкретный пучок полученный сведением именно из задачи (1.12-15). В свете этого сразу получим, что спектр симметричен относительно вещественной оси и , так как это непосредственно проверяется для задачи (1.12-15). Дискретность спектра кроме точек 0 и , есть следствие теоремы 5.1 из примененной к . Утверждение о локализации спектра при больших и малых следует из аналитичности вектор – функции

(2.5)

соответственно в областях .

Функция в (2.5) является сопряженным к оператор функции . Теорема доказана.

При формулировке проводимого ниже утверждения для простоты будем считать, что все с. з. пучка (и задачи 1.12 – 15) простыми. Каждому такому и отвечающему собственному вектору пучка поставим в соответствие вектор из пространства .

Теорема 2. Система векторов отвечающих всем с. з. при полна в с точностью до конечномерного подпространства.

Доказательство. Допустим, что система неполна в указанном пространстве. Тогда согласна лемме 2 из найдутся векторы из которых хотя бы один отличен от нуля, такие что вектор – функция будет аналитична в .

Выбираем достаточно малым, учитывая что имеет конечный порядок роста, и применяя к ней теорему Фрагмена – Линделефа вне области можно получить, что Полученное противоречие доказывает, что система полна в пространстве с точностью до конечномерного подпространства. Теорема доказана.

Замечание. Для того, чтобы сформулировать результат о полноте с конечным дефектом для исходной задачи (1.12-15), нужно проследить за обратным переходом от пучка из (2.4) к этой задаче.

Литература:

1. Копачевский Н. Д., Темнов А. Н. Свободные колебания вязкой стратифицированной жидкости в сосуде – Деп. в ВИНТИ 16.08.33, № 4531-83 ДЕП, 43 с.

2. Копачевский Н. Д., Темнов А. Н. Колебания стратифицированной жидкости в бассейне произвольной формы. – ЖВМ и МФ, 1986, т. 26, № 5.

3. Оразов М. Б. Некоторые вопросы спектральной теории несамосопряженных операторов и связанные с ними задачи механики. - Докт. Дисс., Ашхабад. 1983.

4. Ashirov A. On the problem about fluctuations of the system of a viscous stratified liquid in the elastic vessel. – The IV congress of the Turkic World mathematical society. Book of abstracts. Baku, Azerbaijan, 2011.

5. Краусс В. К. Внутренние волны. – Л., “Гидрометеоиздат”, 1968.

6. Аскеров Н. К., Крейн С. Г., Лаптев Г. И. Задача о колебаниях вязкой жидкости и связанные с ней операторные уравнения -функциональный анализ и его приложения, 1968, т. 2, № 2.

7. Бабский В. Г., Копачевский Н. Д., Мышкис А. Д., Слобожанин Л. А., Тюпцов А. Д. Гидромеханика невесомости. – М., “Наука”, 1976.

8. Гохберг И. Ц, Крейн М. Г. Введение в теорию линейных несамосопряженных операторов, М., “Наука” 1965.

9. Радзиевский Г. В. Квадратичный пучок операторов. – Препринт, Киев 1976.