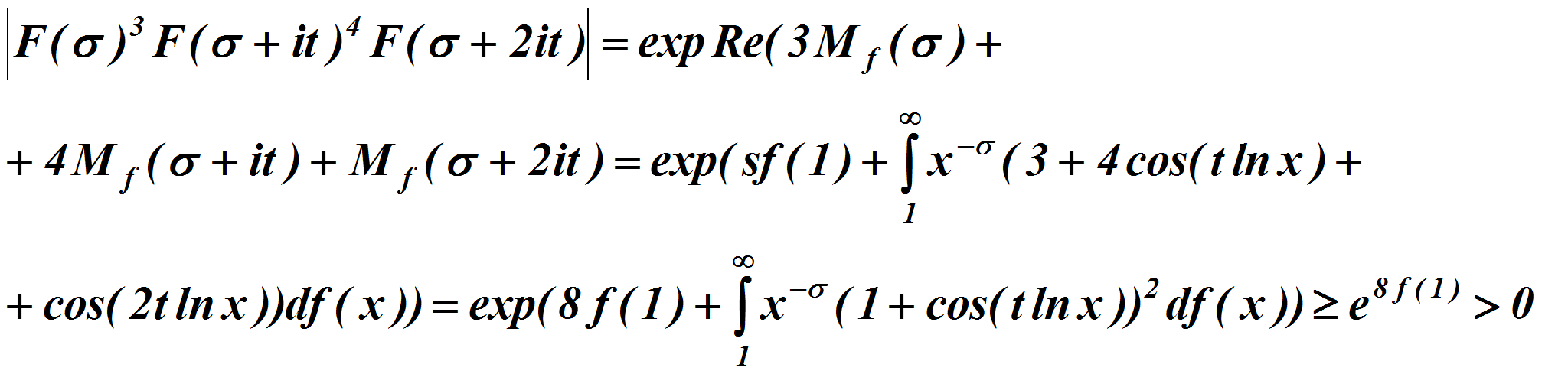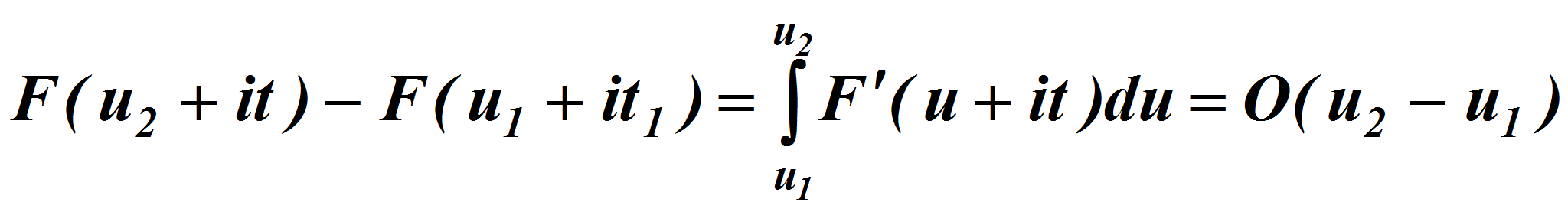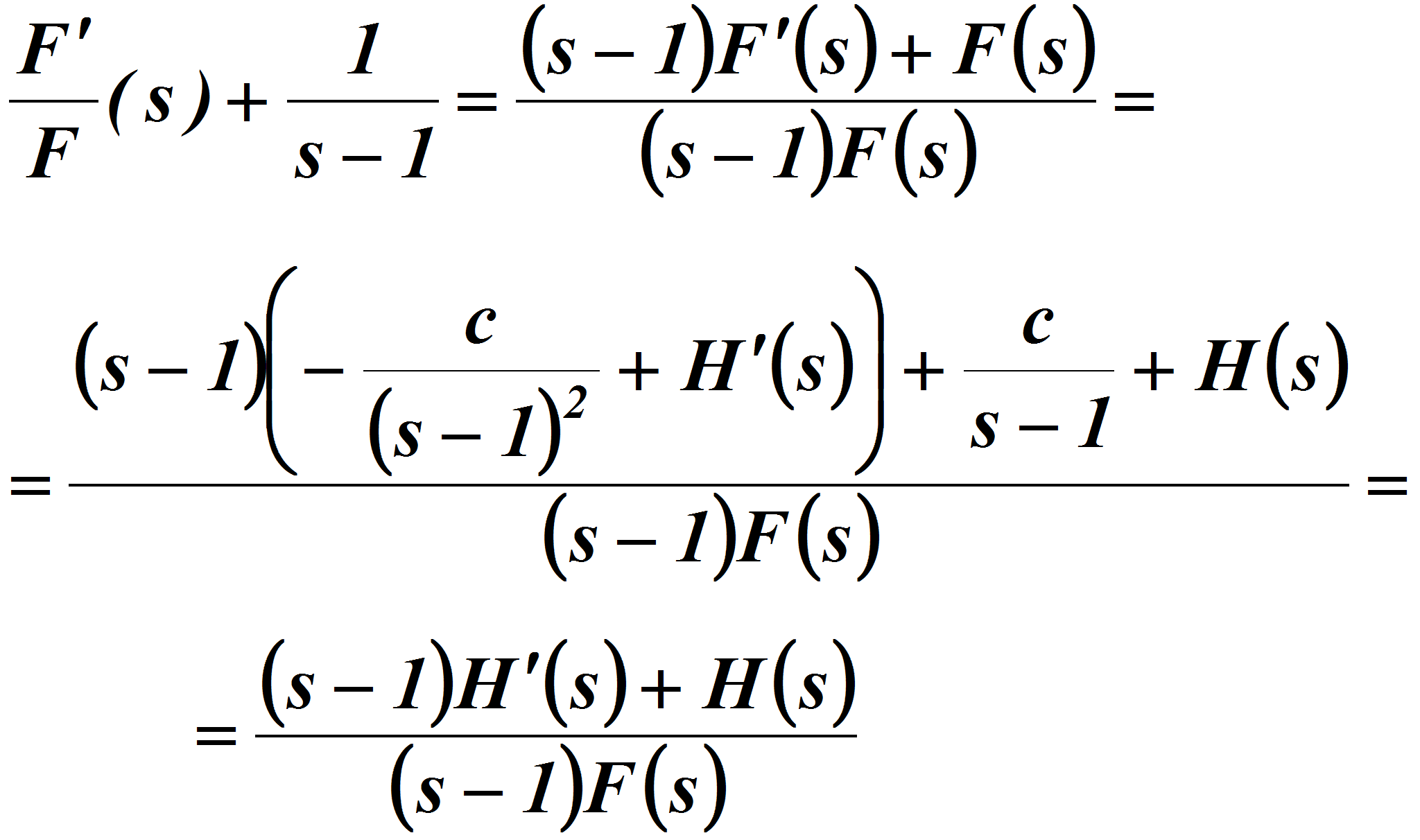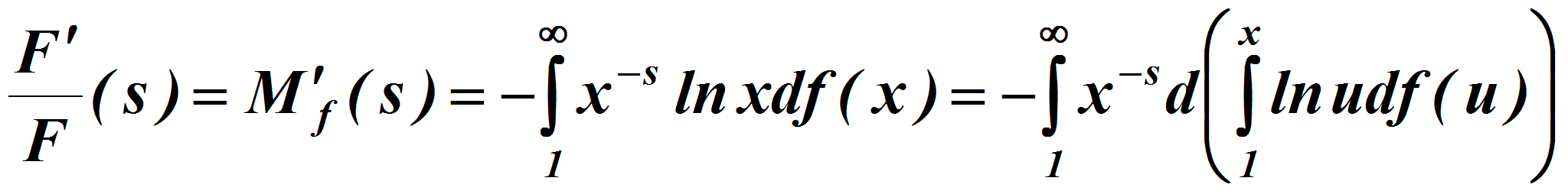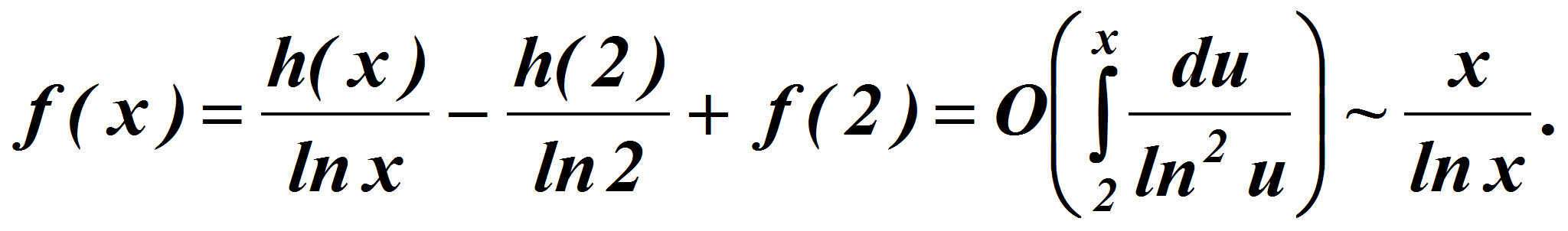The work considers the issue of minimal limitations which the Mellin transformation exponential of non-decreasing function f(x) must be in accord with in order for asymptotic behaviour of this function for large xs to be analogous to asymptotic behaviour of quantity of numbers not exceeding x.
Sufficient conditions which the Mellin transformation of non-decreasing function f(x) must be in accord with in order for asymptotic formula f(x) ≈ x/eux where x → ∞, have been obtained.
From the results obtained, in particular where f(x) = π(x), here is contained the asymptotic law of distribution of prime numbers.
Работа содержит достаточные условия,
которым должно удовлетворять преобразование Меллина неубывающей
функции
![]() ,
чтобы была справедлива асимптотическая формула
,
чтобы была справедлива асимптотическая формула![]() при
при
![]() .
.
Из полученных результатов, в частности, при
![]() здесь содержится асимптотический закон распределения простых чисел.
здесь содержится асимптотический закон распределения простых чисел.
Пусть
![]() −
неубывающая функция, определенная при
−
неубывающая функция, определенная при
![]()
Поставим вопрос о том, какие минимальные ограничения на
функцию
![]() обеспечивают
асимптотическую формулу
обеспечивают
асимптотическую формулу
− аналог закона простых чисел.
Введем следующее определение. Будем говорить, что
функция
![]() ,
регулярная при
,
регулярная при
![]() ,
продолжима на прямую
,
продолжима на прямую
![]() ,
если для каждого фиксированного действительного
,
если для каждого фиксированного действительного
![]() существует конечный предел
существует конечный предел
Если при этом стремление к пределу равномерно в каждом
конечном промежутке изменение
![]() ,
то продолжимость называется равномерной.
,
то продолжимость называется равномерной.
Лемма 1. Пусть
интеграл
![]() сходится при
сходится при
![]() ,
,![]() .
Если производная
.
Если производная
![]() равномерно
продолжима на прямую
равномерно
продолжима на прямую
![]() ,
исключая точку
,
исключая точку
![]() ,
,
при
![]() ,
то функция
,
то функция
![]() не
обращается в нуль в замкнутой плоскости
не
обращается в нуль в замкнутой плоскости
![]() .
.
Доказательство. Из
сходимости интеграла
![]() при
при
![]() ,
следует, что
,
следует, что
![]() при
при
![]() .
Далее
.
Далее
С другой стороны, если
![]() ,
,
![]() ,
то при
,
то при
![]()
Ввиду равномерной продолжимости
производной
![]() на прямую
на прямую
![]() ,
имеем
,
имеем
![]() при
при
![]() ,
откуда следует
,
откуда следует
Отсюда согласно условию леммы вытекает
в противоречии с неравенством (1).
Мы воспользовались тем, что из равномерной продолжимости
![]() следует равномерная продолжимость
следует равномерная продолжимость
![]() ,
так как при
,
так как при
![]()
что влечет за собой равномерную продолжимость функции
![]() ,
и следовательно, оценку
,
и следовательно, оценку
Полученное противоречие показывает, что![]() при
при
![]() .
Лемма доказана.
.
Лемма доказана.
Теорема 1. Если
функция
![]() такова, что
такова, что
![]() ,
при
,
при
![]() ,
причем
,
причем
![]() ,
функция
,
функция
![]() равномерно
продолжима на прямую
равномерно
продолжима на прямую
![]() ,
то
,
то
Доказательство. Из наших условий следует, что
Ввиду равномерной продолжимости функции
![]() из леммы 1 следует, что функция
из леммы 1 следует, что функция
![]() не обращается в нуль в замкнутой полуплоскости
не обращается в нуль в замкнутой полуплоскости
![]() .
Так как при
.
Так как при
![]()
то
Так как числитель и знаменатель последней дроби
равномерно продолжимы на прямую
![]() ,
причем знаменатель
,
причем знаменатель
![]() не обращается в нуль в полуплоскости
не обращается в нуль в полуплоскости
![]() (так как
(так как
![]() ),
то функция
),
то функция
![]() равномерно продолжима на прямую
равномерно продолжима на прямую
![]() .
.
Применим к ней сформулированную ниже теорему Икеара.
Теорема.
(Теорема Икеара [2]). Пусть
![]() неубывающая функция, определенная при
неубывающая функция, определенная при
![]() .
.
Если функция
равномерно продолжима на прямую
![]() ,
то
,
то
![]() при
при
![]() .
.
В нашем случае
так что из предыдущего вытекает, что условия теоремы Икеара выполнены. Согласно этой теоремы
Отсюда следует
откуда
Теорема доказана.
-
- Литература:
Ингам А.Е. Распределение простых чисел.− ОНТИ, 1936.
Райков Д.А. Обобщение теоремы Икеара−Ландау.− Матем. сб. 8(45), №3, 1938, 559-568.
Постников А.Г. Упрощение элементарного доказательства А.Сельберга асимптотического закона распределения простых чисел.− УМН, т.х., 1955, №4.