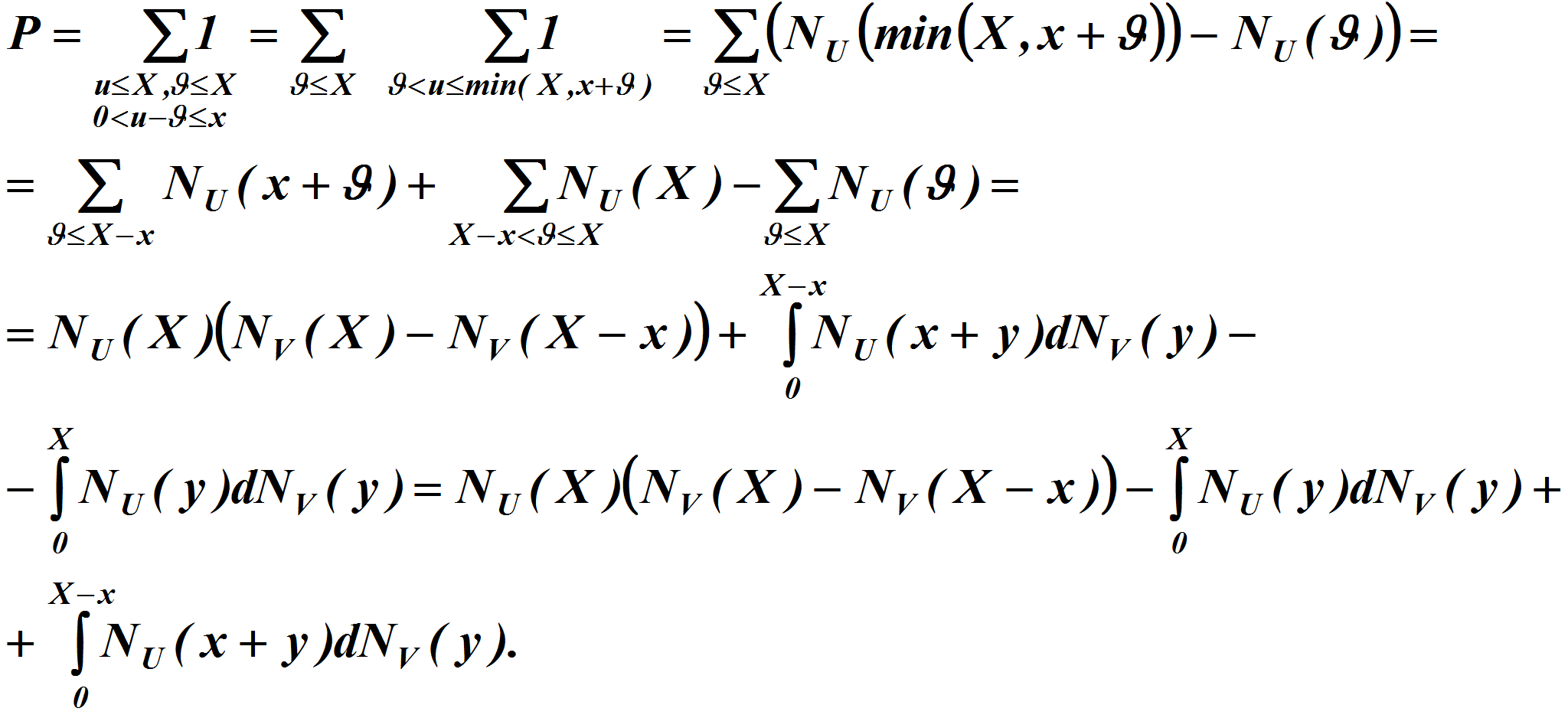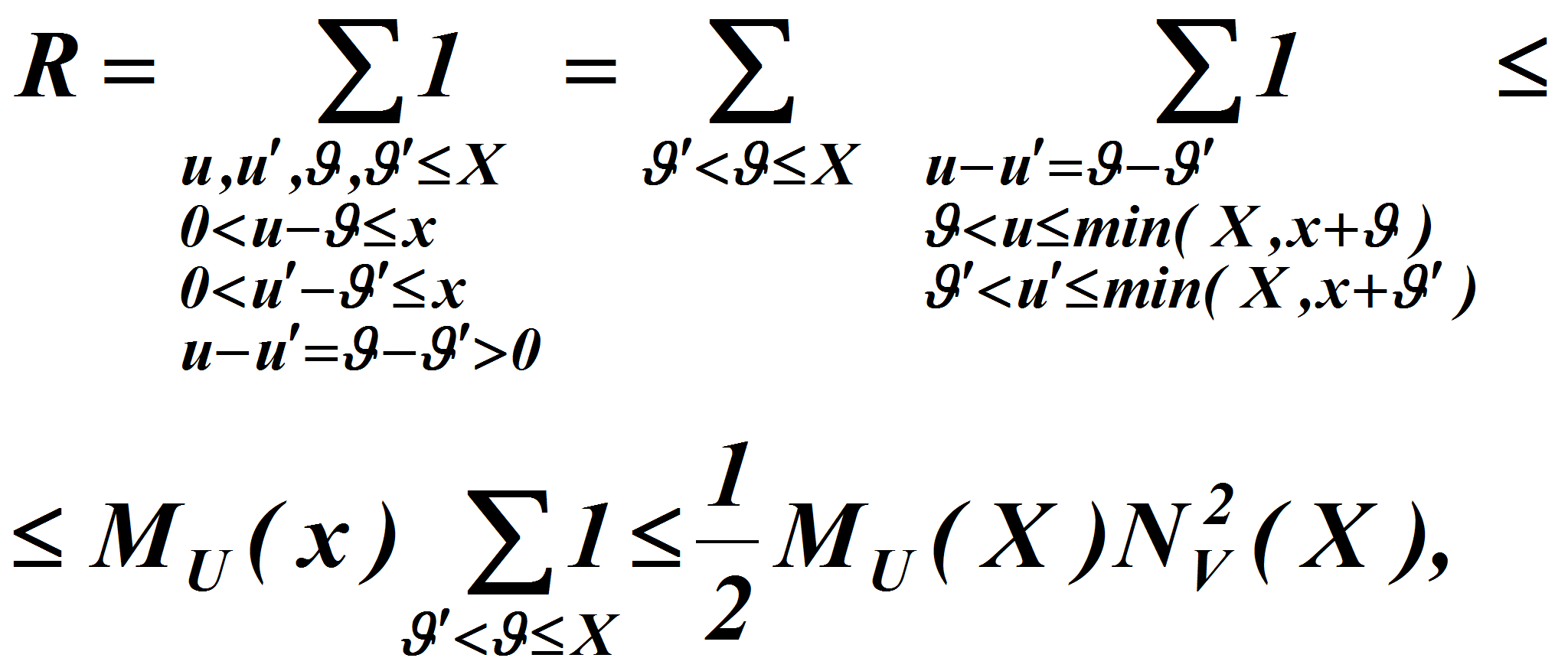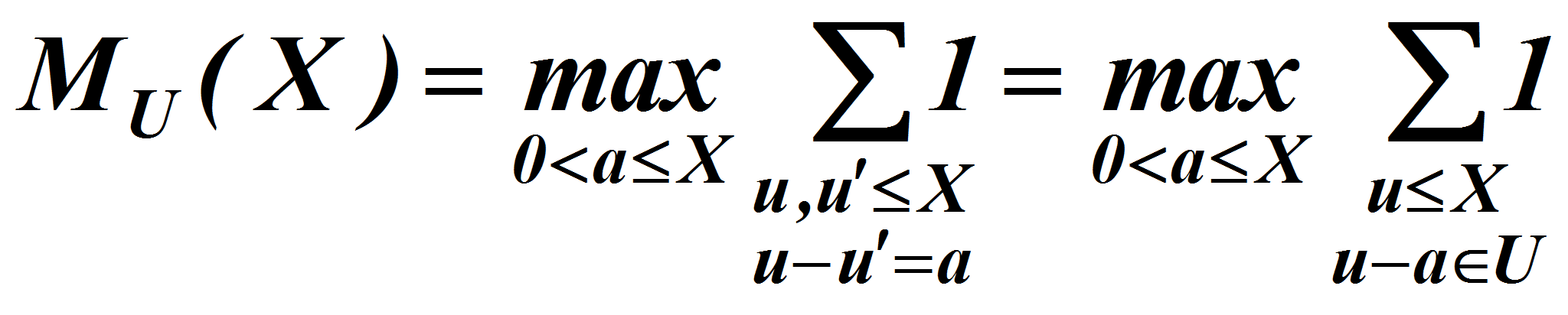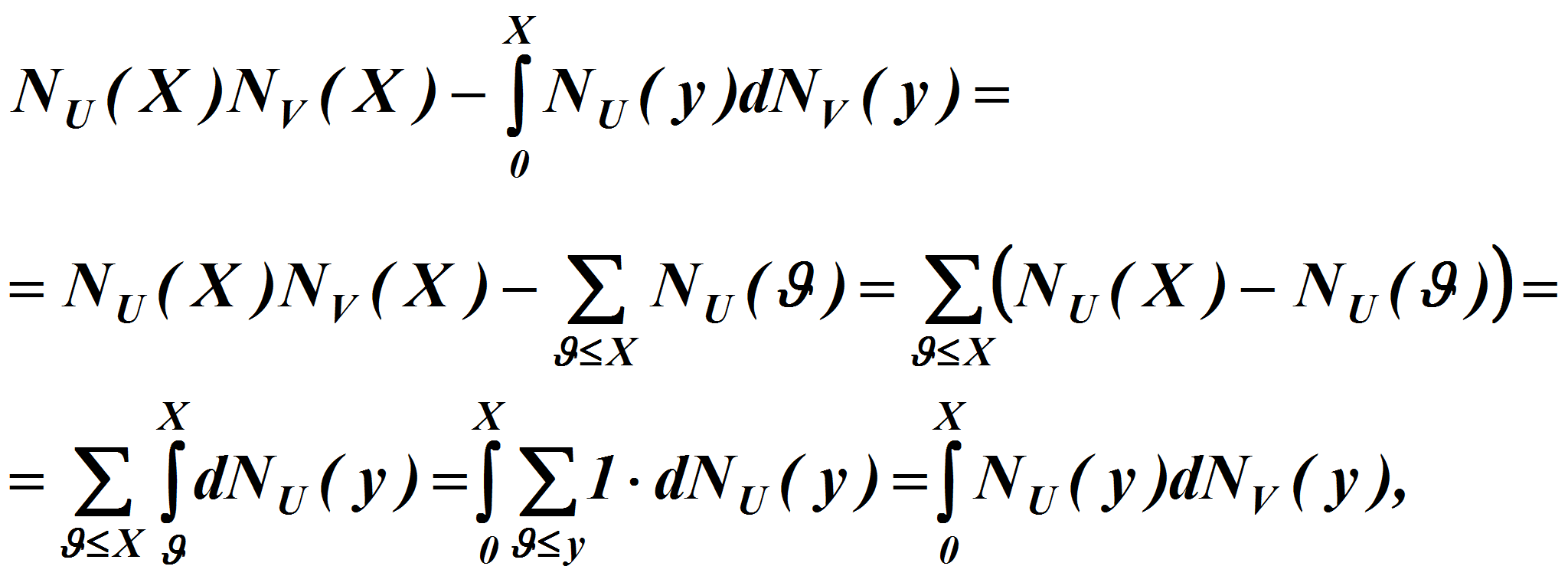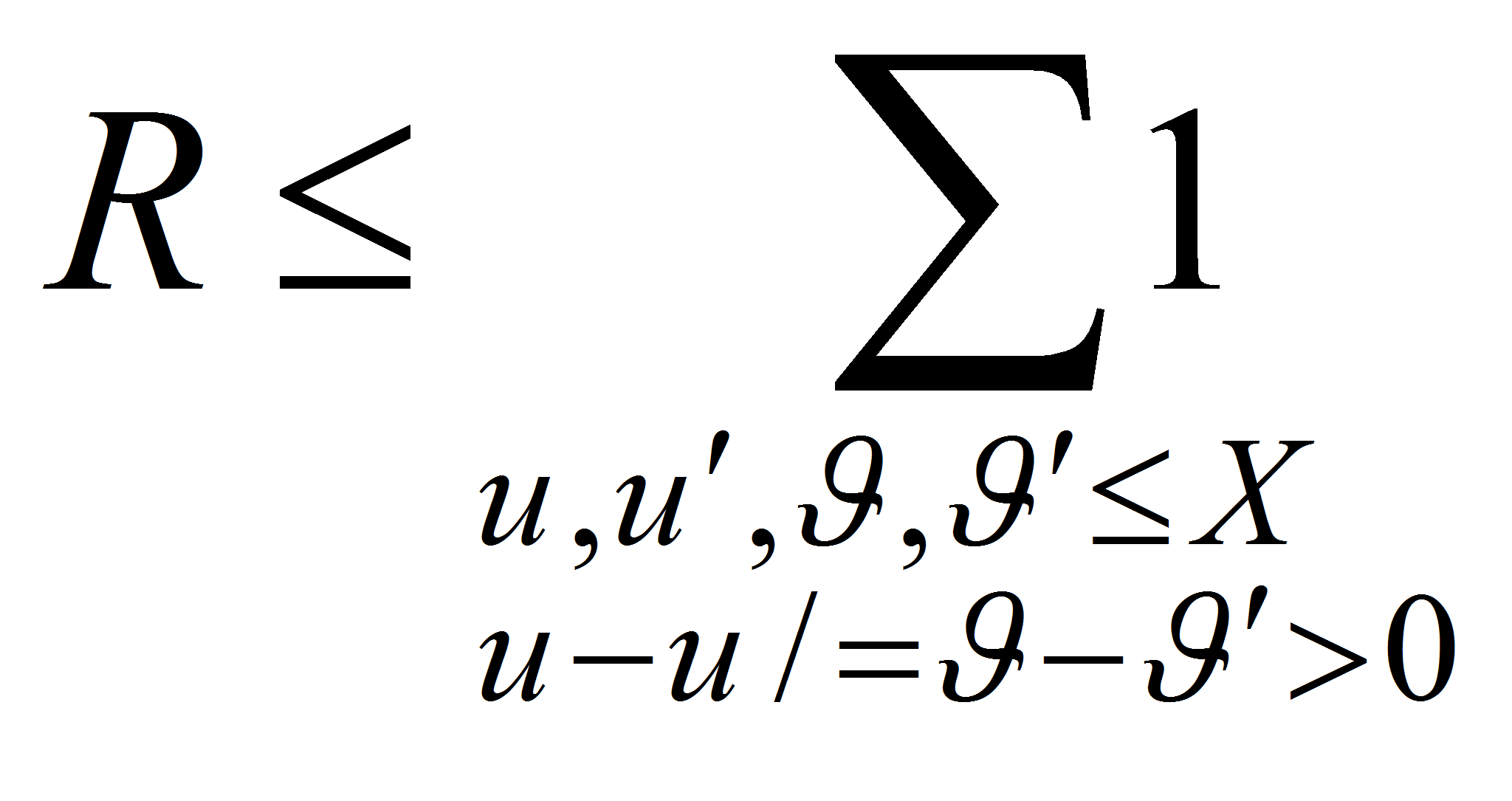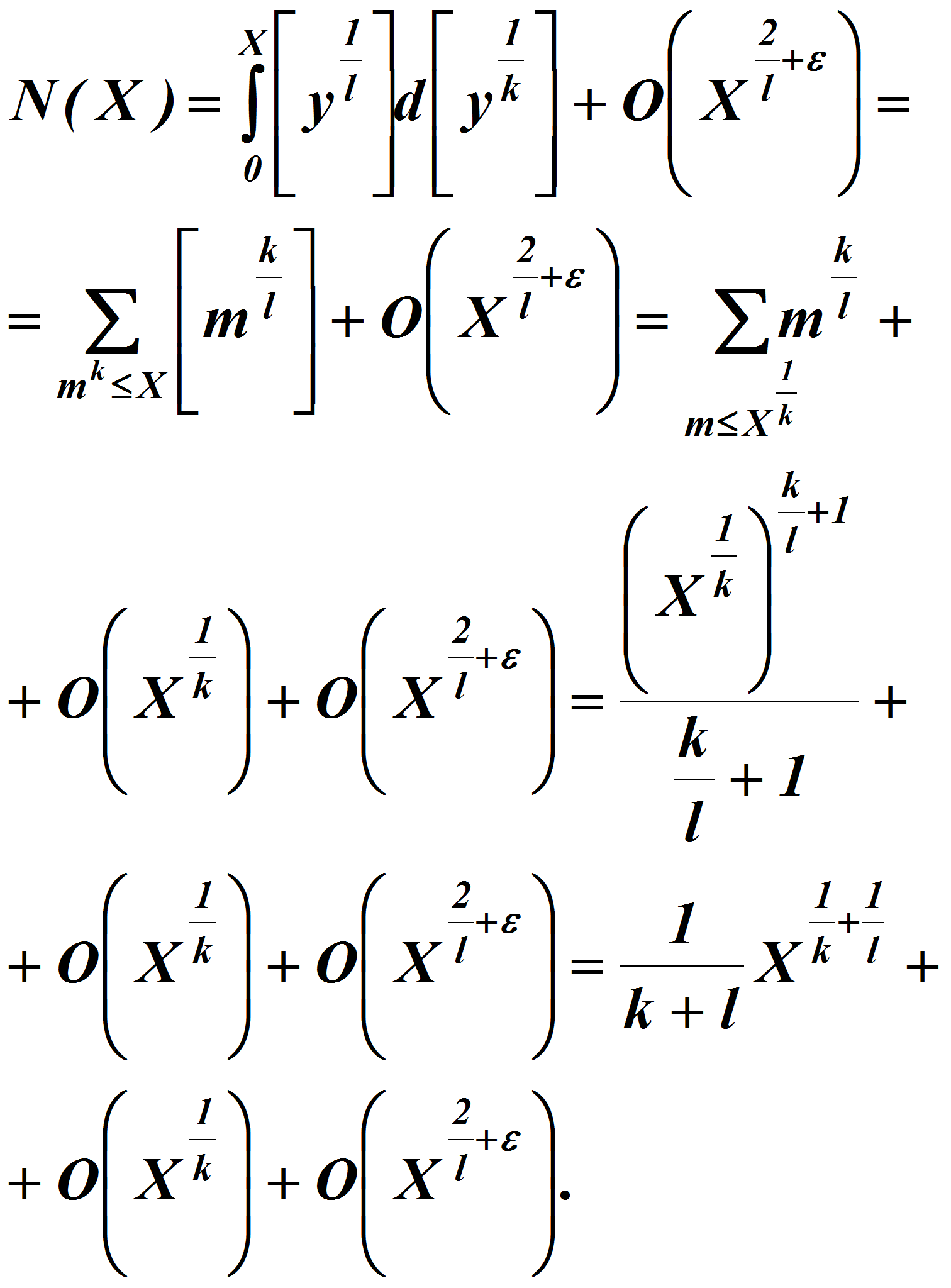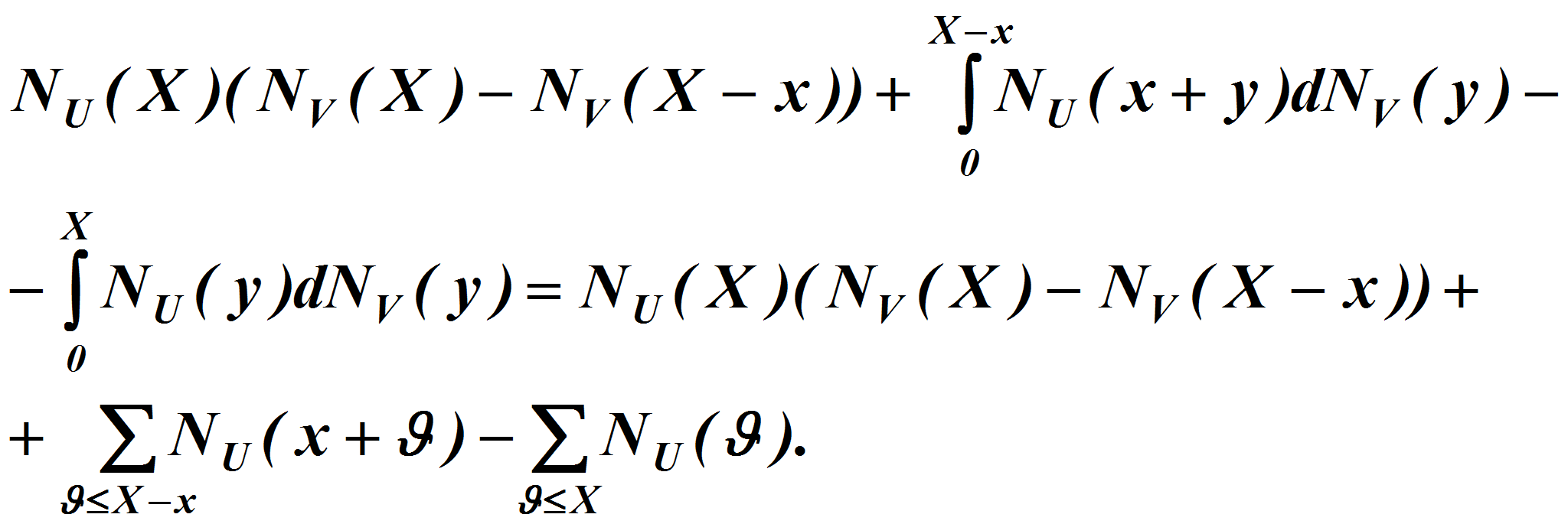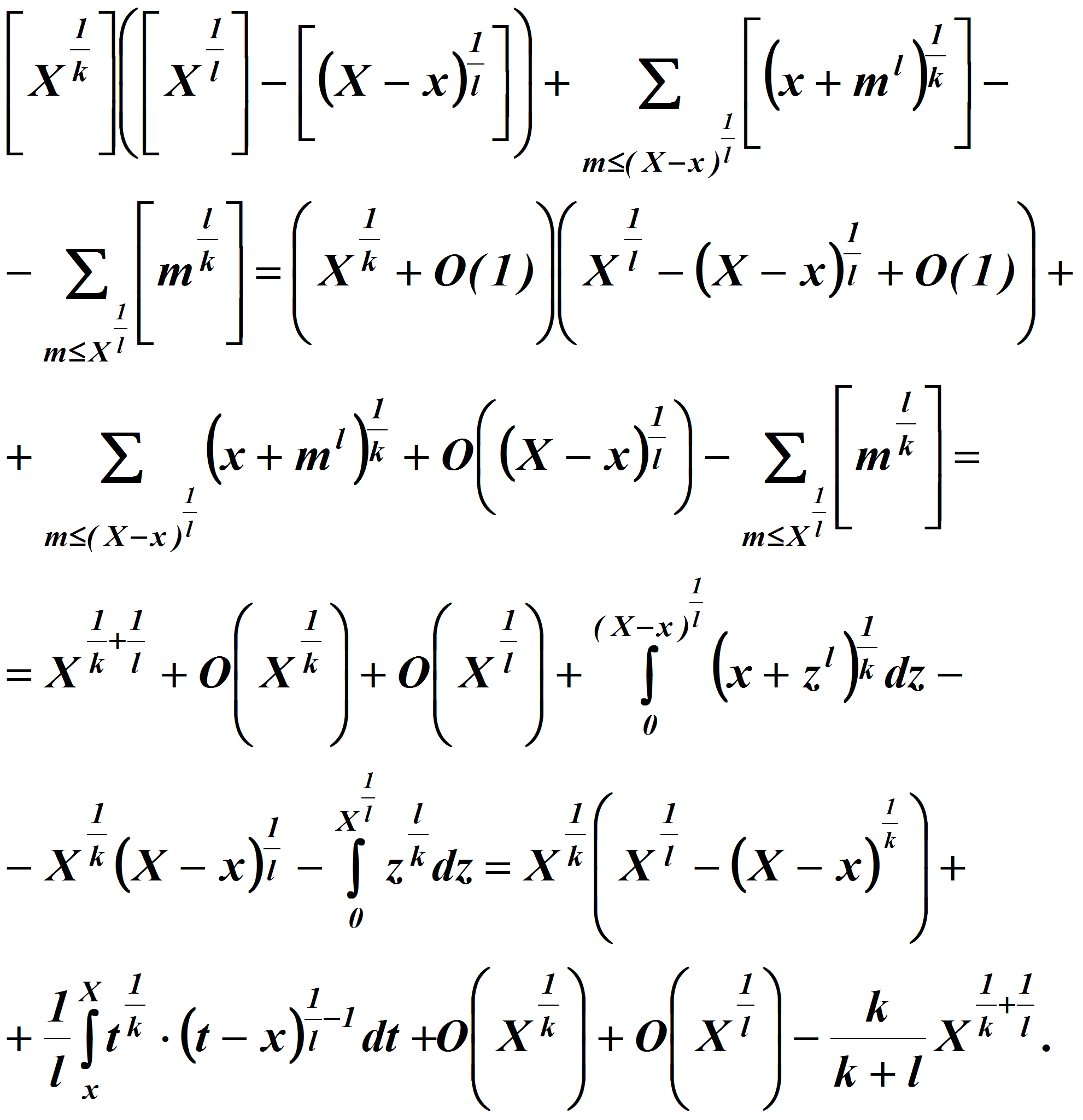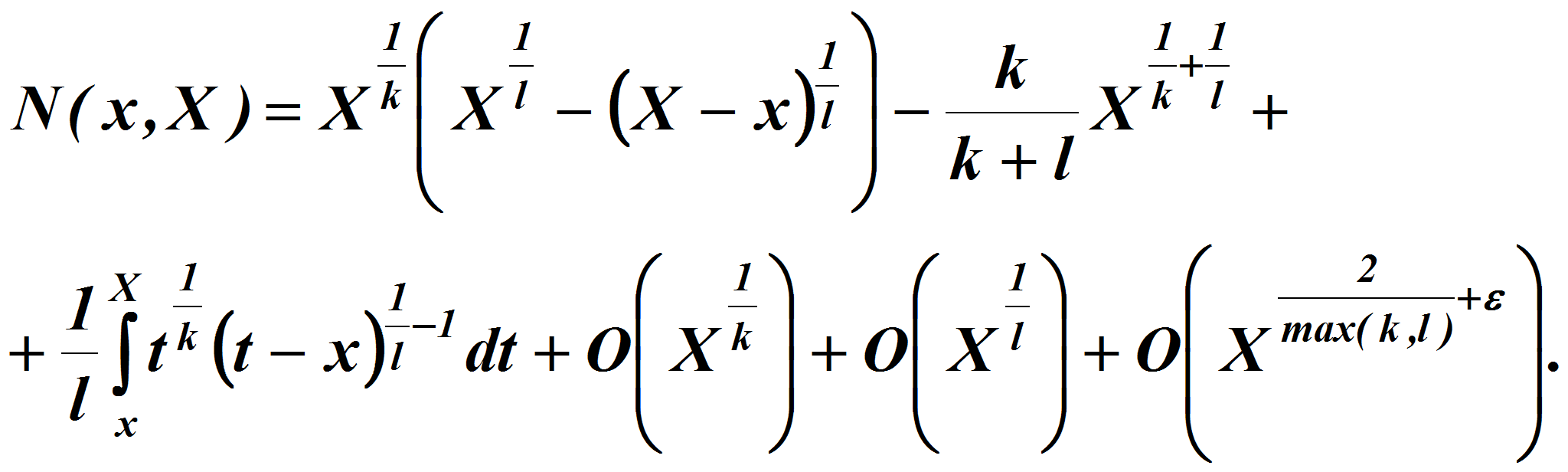The present work
researches the density of sequence of natural numbers, belonging
within a specified interval and presentable as a difference between
members of two specified sequences of natural numbers U
and V.
Using the identical equation of N. P. Romanoff and the Romanoff-Erdцs
inequality asymptotic formulae, characterising the quantity of
natural numbers presentable as a difference of ak
– bl,
where a and
b
– natural numbers, k
≥ 2, l ≥ 2 – whole
numbers, have been obtained. Asymptotic formulae for the quantity of
natural numbers, not exceeding a specified limit and presentable as a
difference u
- ∂, (u
U and ∂
V) in one
way only, have been obtained.
В данной работе изучается плотность
последовательности натуральных чисел, принадлежащих заданному
интервалу и представимых в виде разности членов двух заданных
последовательностей натуральных чисел
и
.
С помощью тождества Н.П.Романова и
неравенства Романова−Эрдоша получены асимптотические формулы,
характеризующие количество натуральных чисел, представимых в виде
разности
,
где
и
− натуральные числа,
,
−
целые числа. Получены также асимптотические формулы для числа
натуральных чисел, непревосходящих заданной границы и представимых в
виде разности
,
(
и
)
единственным образом.
Пусть
и
две последовательности натуральных чисел. Мы рассматриваем
натуральные числа
представимые в виде
,
где
,
(в
дальнейшем включения
и
подразумевается
если явно не оговорено противное).
Применим тождество Романова к множеству
,
образованному парами (
),
где
,
,
и
.
Обозначим через
и
соответственно
подсчитывающие функции последовательностей
а через
&#;
число пар из
.
В этих обозначениях
Обозначим через
число представлений натурального
в виде разности
,
где
,
.
Согласно тождеству Романова [1]
,
где
где
.
Пусть
&#;
число натуральных чисел
,
представимых в виде разности
,
где
,
а
&#;
число натуральных чисел
,
представимых в указанном виде единственным образом. В силу
неравенства Романова&#;Эрдоша
[1]
С другой стороны
Так как
то
Таким образом справедлива
Теорема 1. Имеют место соотношения
где
.
Пусть
означает число натуральных чисел, представимых в виде разности
,
где
,
а
&#;
число натуральных чисел, представимых в указанном виде единственным
образом. Очевидно,
.
Поэтому при
из теоремы 1 следует
Теорема 2. В условиях теоремы 1
и
,
.
Ясно, что последний интеграл
.
С другой стороны, если
,
то
Если существует функция
при
,
такая, что
и
,
то при
имеем
и следовательно
Если при этом
и
,
то
.
Таким образом, имеет место
Теорема 3. Пусть
и
&#;
последовательности натуральных чисел такие, что
и существует функция
(при
),
такая, что
и
.
Тогда при
и
.
Замечание. Как видно
из определения величины
,
.
Последняя сумма симметрична относительно
и
.
Поэтому наряду с оценкой
,
полученной выше, справедливо также неравенство
.
Отсюда следует, что утверждение теоремы 2 остается
справедливым, если в вычитаемых членах заменить
на
.
Ввиду асимметрии исходной задачи относительно
и
,
такая замена позволяет в ряде случаев получать новые результаты.
Применим теорему 2 к последовательностям степеней
,
,
где
и
заданные
целые числа &#;2.
Тогда
,
.
Как было доказано в работе [1], в этом случае
,
,
для любого фиксированного
.
По теореме 2
Если
,
то есть
,
то главный член не поглощается остатком, ввиду
произвольной малости
В силу предыдущих замечаний второй остаточный член можно
заменить на
.
Это соответствует оценке
.
Согласно теореме 2, точно также
получается и оценка
.
Поэтому справедлива следующая
Теорема 4. Пусть
и
неравные друг другу целые числа &#;2.
Тогда число натуральных чисел, непревосходящих
и представимых в виде разности
,
в котором уменьшаемое и вычитаемое также не превосходит
,
а также число натуральных чисел, непревосходящих
и представимых в указанном виде единственным образом асимптотически
равно
,
где
&#;
произвольно малое фиксированное положительное число.
Теоремы 2&#;4
относятся к случаю
.
Рассмотрим теперь задачу о натуральных числах
,
представимых в форме
,
где
и
заданные целые числа,
и
натуральные числа
,
причем
.
Применим теорему 1. Главный член в этой теореме равен
Если
,
,
то последнее выражение равно
Отсюда также, как при доказательстве предыдущей теоремы, имеем
Аналогичные равенства справедливы для
.
-
- Литература:
Оразов М. Некоторые приложения неравенства Романова-Эрдоша.&#; Изв.АН Туркм.ССР, сер. физ.&#;техн., хим. и геолог. Наук 1 (1978), 3&#;9.
Wirzing E. Eine Erweiter und der esten Romanow schen sotzes.&#; Math., 9(1958), 407&#;409.
Бредихин Б.М. Остаточный член в асимптотической формуле для
.&#;
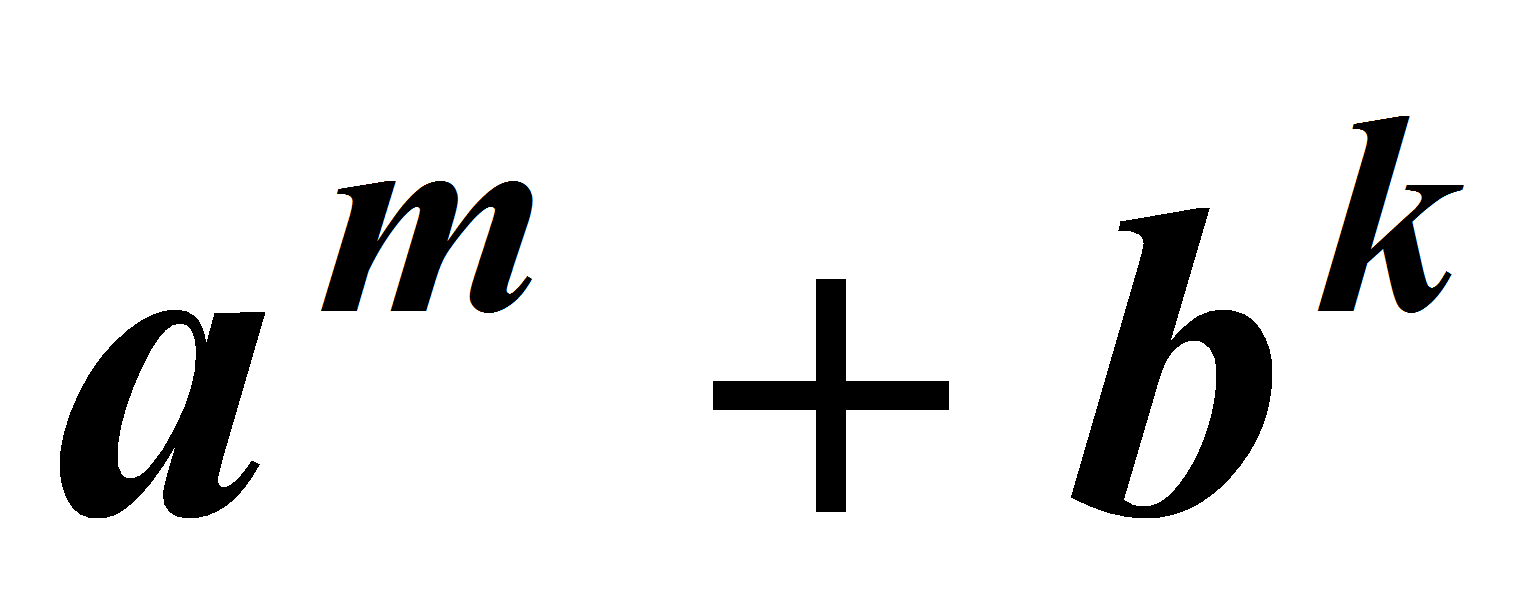Изв. Высших учебных заведений СССР, Математика, 6(19), 1960, 40&#;49.
