В данной работе представлена оценка влияния формы башенной градирни из монолитного железобетона на восприятие ветровых нагрузок. Проведен анализ влияния воздействия ветра на три математические модели башни на основе расчета в программном комплексе SAP 2000 21, с помощью которого были выявлены деформированные схемы башен и распределения напряжений по тему оболочек.
Ключевые слова: напряженно-деформированное состояние, железобетон, башенная градирня, ветровая нагрузка, ветровое воздействие.
При строительстве и проектировании высотных зданий и сооружений существенный вклад в напряженно-деформированное состояние системы вносит ветровое воздействие. Более того, ветровая нагрузка является динамической, восприятие которой может привести к потере устойчивости конструкции и обрушению. В этой связи, возникают вопросы, связанные с обеспечением надежности и безопасности здания или сооружения на всех их жизненных этапах с помощью влияния внешней формы сооружения.
Основная часть
В рамках статьи рассматривался вопрос влияния формы башенной оросительной градирни на восприятие ветровой нагрузки.
Параметр высоты оболочки был принят одинаковым для всех рассматриваемых моделей и равен 100,0 м. Радиус основания оболочек принят равным 50,0 м для всех вариантов. Высота опорной колоннады 15 м, следовательно, суммарная высота градирни от уровня земли составляет 115,0 м.
Толщина стенки железобетонной оболочки по п.6.3.3 [1] должна быть не менее 180 мм и иметь переменное сечение по высоте, но, так как подбор сечения производиться не будет, для обеспечения равенства условий восприятия нагрузки, принимаем толщину оболочки равной 250 мм для всех трех вариантов. Опорный пояс имеет прямоугольное поперечное сечение размерами 800х600 мм. Наклонная опорная колоннада устроена по касательной к нижней грани оболочки и имеет прямоугольное поперечное сечение размерами 450х450 мм. Прочие параметры градирен определены математическим расчетом и приведены ниже в таблице 1.
Материал оболочки и опорного пояса, а также для опорной колоннады и кольцевого фундамента по п.6.6.8 [1] принимается бетон класса прочности на осевое сжатие В30.
Определение размеров башенных градирен
Башня градирни представляет собой однополостной гиперболоид, описываемый следующим математическим уравнением в декартовых координатах:
где А и В — действительные полуоси,
С — мнимая полуось,
х, y, z — координаты точек поверхности.
Для упрощения, гиперболоид может быть построен как фигура вращения с формообразующей гиперболой, подчиняющейся уравнениям:
![]() (2)
(2)
или ![]() (3)
(3)
При этом, параметр С будет отвечать за масштаб значения Z, а параметры А и В — за пологость формы. Таким образом, можно задать формообразующие разной степени изгиба. Чем меньше значение параметров А и В, тем больше перепад в значениях Z.
Вращение гипербол (2,3) осуществляется вокруг осей, параллельных OX или OY соответственно. Вершина гиперболы будет приходиться на точку с координатой по осям OX/OY соответствующей 0. Для формирования оболочки градирни, минимальный диаметр располагается примерно на ¼ ниже верха башни, следовательно, для распределения высот будут использоваться как положительные, так и отрицательные значения. Шаг по вертикали для упрощения принимаем равным 5м, нижний диаметр будет определяться значением при X = -75м, верхний при Х = +25 м.
Принимаем параметр масштаба С равным 10. Параметр изгиба формообразующей кривой принимаем равной 12,5; 13,75 и 15. На основе расчета получаем следующие значения координаты Z, приведенные на рисунках 1, 2, 3.
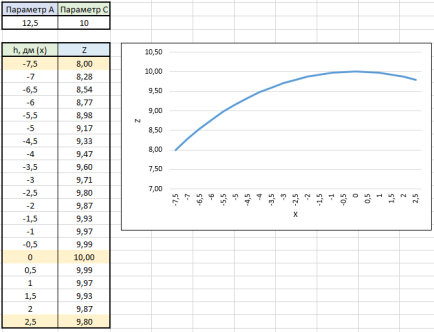
Рис. 1. Форма гиперболы при А = 12,5
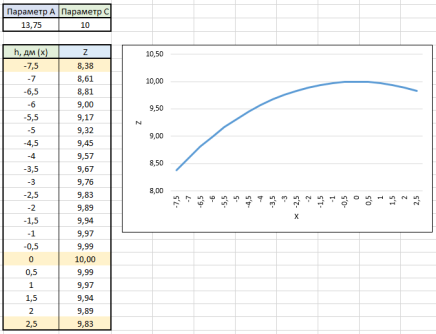
Рис. 2. Форма гиперболы при А = 13,75
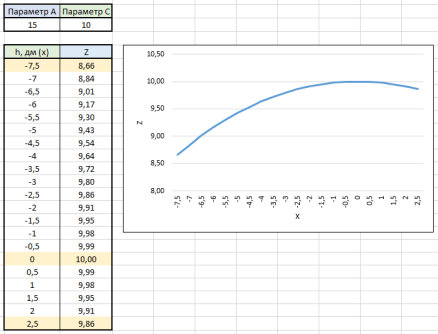
Рис. 3. Форма гиперболы при А = 15
Согласно вычисленным параметрам градирен, определяем физические значения радиусов участков башни для построения в графическом программном комплексе (табл. 1). Параметры определялись пропорционально относительно известного размера нижнего радиуса поверхности.
Таблица 1
Параметрические и физические параметры башенных оросительных градирен
|
Вариант оболочки |
Параметр А |
Радиус в основании, м |
Радиус в верхней части, м |
Радиус самой узкой части, м |
Вспомогательная точка построения |
|
1 |
12,5 |
50 |
32 |
30 |
-5: 38 м |
|
2 |
13,75 |
50 |
36 |
34 |
-5: 41 м |
|
3 |
15 |
50 |
38 |
37 |
-5: 43м |
Расчетные модели оболочек были разработаны в графическом программном комплексе Rhinoceros 6 и экспортированы в расчетный комплекс, реализующий МКЭ, SAP 2000 21.
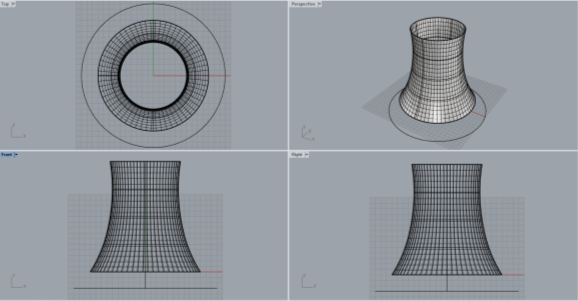
Рис. 4. Моделирование оболочки в ПК Rhinoceros 6
Стержневая опорная колоннада и опорный пояс заданы универсальным линейным конечным элементом Straight Frame, сетка оболочки задана универсальным пластинчатым конечным элементом Shell Thin, размеры сетки 5х5 м.
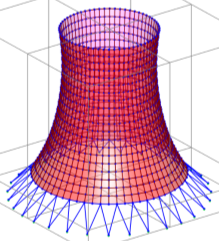
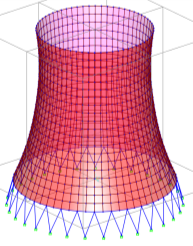
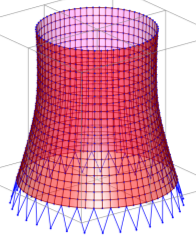
Рис. 5. Модели оболочек в ПК SAP 2000 21
Опорные закрепления не допускают линейных перемещений в трех направлениях, а также повороты относительно этих трех направлений.
Сбор нагрузок
Расчет градирен проводился на восприятие собственного веса конструкций, который задается автоматически в ПК SAP 2000 21 на основе заданного материала и размеров поперечных сечений всех элементов, и ветрового воздействия. Статическая ветровая нагрузка собиралась для г. Санкт-Петербурга типа местности А в соответствии с [2], динамическая составляющая задавалась автоматически в ПК SAP 2000 21.
Так как ветровое давление в ПК SAP 2000 21 задается параметрально уже с учетом распределения его по высоте конструкции, суть сводится к определению аэродинамического коэффициента се1 внешнего давления по формуле В.2 и аэродинамического коэффициента лобового сопротивления сх по формуле В.3 п. В.1.12 прил. В [2].
Коэффициент лобового сопротивления сх для наклонных элементов определяется по формуле В.4. п. В.1.12 прил. В [2] и зависит от вертикального угла наклона оси элемента к горизонтальной плоскости.
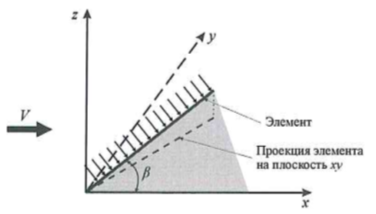
Рис. 6. Значение вертикального угла при определении коэффициента сх
Определение коэффициента сх приведено в таблице 2.
Таблица 2
Определение коэффициента лобового сопротивления сх
|
Вариант 1 |
|||||||||
|
Δ |
z |
d, m |
k(z) |
Re*10–6 |
Δ/d |
C |
β верт |
sinβв |
Сx |
|
0 |
15 |
100 |
1,125 |
3,514 |
0,00000200 |
0,4 |
45 |
0,707 |
0,283 |
|
4,46 |
19,46 |
94,71 |
1,237 |
3,759 |
0,00000211 |
0,4 |
59,3 |
0,860 |
0,344 |
|
4,56 |
24,02 |
89,76 |
1,300 |
3,848 |
0,00000223 |
0,4 |
61,54 |
0,879 |
0,352 |
|
4,66 |
28,68 |
85,19 |
1,359 |
3,917 |
0,00000235 |
0,4 |
63,85 |
0,898 |
0,359 |
|
4,75 |
33,43 |
81 |
1,418 |
3,986 |
0,00000247 |
0,4 |
66,23 |
0,915 |
0,366 |
|
4,83 |
38,26 |
77,24 |
1,478 |
4,058 |
0,00000259 |
0,4 |
68,71 |
0,932 |
0,373 |
|
4,91 |
43,17 |
73,91 |
1,532 |
4,113 |
0,00000271 |
0,4 |
71,26 |
0,947 |
0,379 |
|
4,98 |
48,15 |
71 |
1,582 |
4,163 |
0,00000282 |
0,4 |
73,73 |
0,960 |
0,384 |
|
5,03 |
53,18 |
68,49 |
1,632 |
4,218 |
0,00000292 |
0,4 |
75,99 |
0,970 |
0,388 |
|
5,07 |
58,25 |
66,34 |
1,683 |
4,281 |
0,00000301 |
0,4 |
78,04 |
0,978 |
0,391 |
|
5,11 |
63,36 |
64,52 |
1,725 |
4,329 |
0,00000310 |
0,4 |
79,89 |
0,984 |
0,394 |
|
5,13 |
68,49 |
63 |
1,764 |
4,373 |
0,00000317 |
0,4 |
81,55 |
0,989 |
0,396 |
|
5,15 |
73,64 |
61,77 |
1,802 |
4,425 |
0,00000324 |
0,4 |
83,2 |
0,993 |
0,397 |
|
5,17 |
78,81 |
60,85 |
1,841 |
4,486 |
0,00000329 |
0,4 |
84,92 |
0,996 |
0,398 |
|
5,18 |
83,99 |
60,26 |
1,880 |
4,559 |
0,00000332 |
0,4 |
86,73 |
0,998 |
0,399 |
|
5,18 |
89,17 |
60,01 |
1,919 |
4,643 |
0,00000333 |
0,4 |
88,62 |
1,000 |
0,400 |
|
5,19 |
94,36 |
60,11 |
1,958 |
4,741 |
0,00000333 |
0,4 |
90,59 |
1,000 |
0,400 |
|
5,18 |
99,54 |
60,57 |
1,997 |
4,854 |
0,00000330 |
0,4 |
92,54 |
0,999 |
0,400 |
|
5,17 |
104,71 |
61,38 |
2,024 |
4,952 |
0,00000326 |
0,4 |
94,46 |
0,997 |
0,399 |
|
5,16 |
109,87 |
62,53 |
2,049 |
5,062 |
0,00000320 |
0,4 |
96,33 |
0,994 |
0,398 |
|
5,13 |
115 |
64 |
2,075 |
5,185 |
0,00000313 |
0,4 |
98,18 |
0,990 |
0,396 |
|
Вариант 2 |
|||||||||
|
Δ |
z |
d, m |
k(z) |
Re*10–6 |
Δ/d |
C |
β верт |
sinβв |
Сx |
|
0 |
15 |
100 |
1,125 |
3,514 |
0,00000200 |
0,4 |
51,93 |
0,787 |
0,315 |
|
4,7 |
19,7 |
95,95 |
1,243 |
3,802 |
0,00000208 |
0,4 |
66,7 |
0,918 |
0,367 |
|
4,75 |
24,45 |
92,17 |
1,306 |
3,915 |
0,00000217 |
0,4 |
68,31 |
0,929 |
0,372 |
|
4,81 |
29,26 |
88,67 |
1,366 |
4,017 |
0,00000226 |
0,4 |
69,97 |
0,940 |
0,376 |
|
4,86 |
34,12 |
85,45 |
1,427 |
4,119 |
0,00000234 |
0,4 |
71,69 |
0,949 |
0,380 |
|
4,9 |
39,02 |
82,54 |
1,488 |
4,222 |
0,00000242 |
0,4 |
73,46 |
0,959 |
0,383 |
|
4,95 |
43,97 |
79,94 |
1,540 |
4,300 |
0,00000250 |
0,4 |
75,28 |
0,967 |
0,387 |
|
4,98 |
48,95 |
77,64 |
1,590 |
4,375 |
0,00000258 |
0,4 |
77 |
0,974 |
0,390 |
|
5,01 |
53,96 |
75,61 |
1,640 |
4,453 |
0,00000265 |
0,4 |
78,57 |
0,980 |
0,392 |
|
5,04 |
59 |
73,83 |
1,690 |
4,536 |
0,00000271 |
0,4 |
79,97 |
0,985 |
0,394 |
|
5,06 |
64,06 |
72,27 |
1,730 |
4,595 |
0,00000277 |
0,4 |
81,21 |
0,988 |
0,395 |
|
5,07 |
69,13 |
70,9 |
1,768 |
4,651 |
0,00000282 |
0,4 |
82,33 |
0,991 |
0,396 |
|
5,08 |
74,21 |
69,76 |
1,807 |
4,713 |
0,00000287 |
0,4 |
83,56 |
0,994 |
0,397 |
|
5,1 |
79,31 |
68,86 |
1,845 |
4,782 |
0,00000290 |
0,4 |
85 |
0,996 |
0,398 |
|
5,11 |
84,42 |
68,27 |
1,883 |
4,860 |
0,00000293 |
0,4 |
86,66 |
0,998 |
0,399 |
|
5,11 |
89,53 |
68,01 |
1,921 |
4,950 |
0,00000294 |
0,4 |
88,54 |
1,000 |
0,400 |
|
5,11 |
94,64 |
68,11 |
1,960 |
5,052 |
0,00000294 |
0,4 |
90,59 |
1,000 |
0,400 |
|
5,11 |
99,75 |
68,58 |
1,998 |
5,169 |
0,00000292 |
0,4 |
92,62 |
0,999 |
0,400 |
|
5,1 |
104,85 |
69,39 |
2,024 |
5,267 |
0,00000288 |
0,4 |
94,56 |
0,997 |
0,399 |
|
5,08 |
109,93 |
70,54 |
2,050 |
5,377 |
0,00000284 |
0,4 |
96,43 |
0,994 |
0,397 |
|
5,06 |
114,99 |
72 |
2,075 |
5,500 |
0,00000278 |
0,4 |
98,22 |
0,990 |
0,396 |
|
Вариант 3 |
|||||||||
|
Δ |
z |
d, m |
k(z) |
Re*10–6 |
Δ/d |
C |
β верт |
sinβв |
Сx |
|
0 |
15 |
100 |
1,125 |
3,514 |
0,00000200 |
0,4 |
75,07 |
0,966 |
0,386 |
|
4,85 |
19,85 |
96,98 |
1,246 |
3,834 |
0,00000206 |
0,4 |
72,7 |
0,955 |
0,382 |
|
4,87 |
24,72 |
94,12 |
1,309 |
3,967 |
0,00000212 |
0,4 |
73,64 |
0,960 |
0,384 |
|
4,89 |
29,61 |
91,4 |
1,370 |
4,092 |
0,00000219 |
0,4 |
74,46 |
0,963 |
0,385 |
|
4,91 |
34,52 |
88,8 |
1,432 |
4,214 |
0,00000225 |
0,4 |
75,13 |
0,967 |
0,387 |
|
4,92 |
39,44 |
86,28 |
1,493 |
4,332 |
0,00000232 |
0,4 |
75,68 |
0,969 |
0,388 |
|
4,93 |
44,37 |
83,85 |
1,544 |
4,416 |
0,00000239 |
0,4 |
76,15 |
0,971 |
0,388 |
|
4,95 |
49,32 |
81,55 |
1,593 |
4,494 |
0,00000245 |
0,4 |
76,91 |
0,974 |
0,390 |
|
4,97 |
54,29 |
79,45 |
1,643 |
4,574 |
0,00000252 |
0,4 |
78,09 |
0,978 |
0,391 |
|
4,99 |
59,28 |
77,63 |
1,693 |
4,659 |
0,00000258 |
0,4 |
79,68 |
0,984 |
0,394 |
|
5,02 |
64,3 |
76,18 |
1,732 |
4,723 |
0,00000263 |
0,4 |
81,71 |
0,990 |
0,396 |
|
5,05 |
69,35 |
75,12 |
1,770 |
4,792 |
0,00000266 |
0,4 |
84,06 |
0,995 |
0,398 |
|
5,06 |
74,41 |
74,45 |
1,808 |
4,873 |
0,00000269 |
0,4 |
86,21 |
0,998 |
0,399 |
|
5,07 |
79,48 |
74,09 |
1,846 |
4,964 |
0,00000270 |
0,4 |
87,95 |
0,999 |
0,400 |
|
5,08 |
84,56 |
73,96 |
1,884 |
5,062 |
0,00000270 |
0,4 |
89,27 |
1,000 |
0,400 |
|
5,08 |
89,64 |
73,99 |
1,922 |
5,165 |
0,00000270 |
0,4 |
90,19 |
1,000 |
0,400 |
|
5,08 |
94,72 |
74,13 |
1,960 |
5,272 |
0,00000270 |
0,4 |
90,78 |
1,000 |
0,400 |
|
5,08 |
99,8 |
74,38 |
1,999 |
5,384 |
0,00000269 |
0,4 |
91,39 |
1,000 |
0,400 |
|
5,07 |
104,87 |
74,75 |
2,024 |
5,467 |
0,00000268 |
0,4 |
92,13 |
0,999 |
0,400 |
|
5,07 |
109,94 |
75,29 |
2,050 |
5,556 |
0,00000266 |
0,4 |
93,01 |
0,999 |
0,399 |
|
5,06 |
115 |
76 |
2,075 |
5,651 |
0,00000263 |
0,4 |
94,02 |
0,998 |
0,399 |
Коэффициент внешнего давления се1 зависит от горизонтального угла , замеряемого до каждого конечного элемента оболочки. Коэффициенты определяются по графику на рис. В.16 п. В.1.12 прил. В [2] в зависимости от числа Рейнольдса Re.
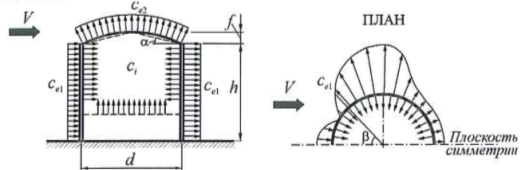
Рис. 7. Схема распределения ветрового давления по цилиндрической поверхности
Определение коэффициента се1 приведено в таблице 3.
Таблица 3
Определение коэффициента внешнего давления се1
|
β гор |
се1 |
β гор |
се1 |
β гор |
се1 |
β гор |
се1 |
|
0 |
1,000 |
48 |
-0,633 |
96 |
-1,265 |
144 |
-0,700 |
|
6 |
0,800 |
54 |
-0,844 |
102 |
-1,124 |
150 |
-0,700 |
|
12 |
0,600 |
60 |
-1,056 |
108 |
-0,983 |
156 |
-0,700 |
|
18 |
0,400 |
66 |
-1,267 |
114 |
-0,841 |
162 |
-0,700 |
|
24 |
0,200 |
72 |
-1,478 |
120 |
-0,700 |
168 |
-0,700 |
|
30 |
0,000 |
78 |
-1,689 |
126 |
-0,700 |
174 |
-0,700 |
|
36 |
-0,211 |
84 |
-1,548 |
132 |
-0,700 |
180 |
-0,700 |
|
42 |
-0,422 |
90 |
-1,406 |
138 |
-0,700 |
В результате модального расчета имеем следующие деформационные схемы и напряженные состояния в оболочке, приведенные на рисунках 8, 9 и 10.
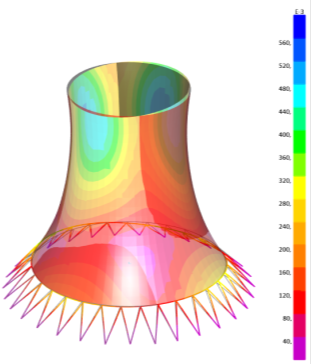
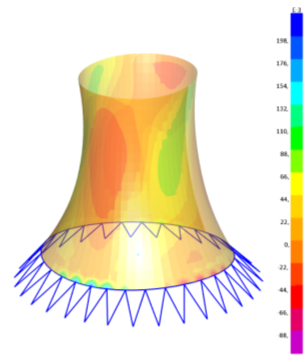
Рис. 8. Деформированная схема и напряжения в оболочке вариант 1
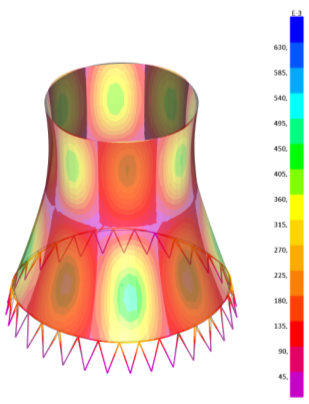
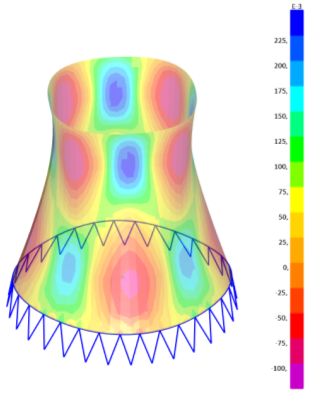
Рис. 9. Деформированная схема и напряжения в оболочке вариант 2
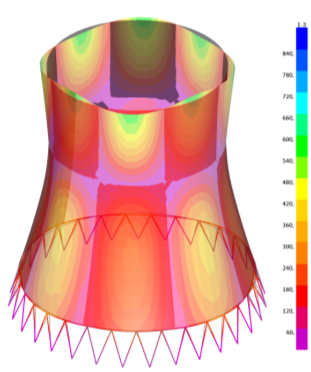
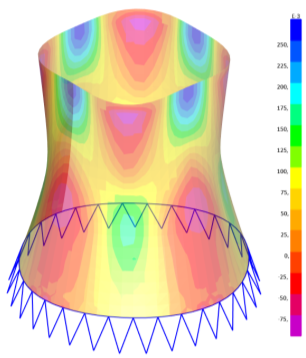
Рис. 10. Деформированная схема и напряжения в оболочке вариант 3
Заключение
Анализируя полученные выше результаты, можно сделать следующие выводы:
- При прочих равных параметрах (материал, высота, диаметр основания), чем более обтекаемую форму имеет оболочка, тем меньшие перемещения в ней возникают в результате восприятия ветрового воздействия;
- Растягивающие и сжимающие напряжения имеют меньше очагов распределения по поверхности оболочки, а также имеют меньшие значения, в случае, если формообразующая гипербола имеет большую стрелу подъема;
- С увеличением пологости оболочки, увеличиваются растягивающие напряжения в бетоне.
Следовательно, оболочка варианта 1 является наиболее рациональной для восприятия ветровой нагрузки в регионе г. Санкт-Петербурга. Тем не менее, форма не соответствует технологически принятым рекомендациям по проектированию башенных градирен, поэтому должна утверждаться технологами с учетом обеспечения требуемой площади орошения и испарения, а также с учетом обеспечения охлаждения воды до требуемой температуры. Более того, подобное расположение опорной колоннады, обеспечивающее осевую передачу усилия от опорного пояса на фундамент, будет требовать серьезной анкеровки, поскольку угол наклона к горизонту достаточно мал, что может значительно сказаться на стоимости сооружения. Таким образом, опираться только на рациональность при восприятии ветровой нагрузки при проектировании башенных градирен нельзя, необходимо учитывать сопутствующие конструктивные параметры и их рациональность.
Литература:
- СП 340.1325800.2017 Конструкции железобетонные и бетонные градирен. Правила проектирования — М.: Минстрой России, 2017. — 48 с.
- СП 20.13330.2016 Нагрузки и воздействия. Актуализированная редакция СНиП 2.01.07–85* — М.: Минстрой России, 2016. — 104 с.
- СНиП 52–01–2003. Бетонные и железобетонные конструкции. Основные положения [Текст]. — М., 2004. — 24 с.
- Югов А. М., Титков С. О., Анищенков В. М. Оценка влияния формообразования башенной металлической градирни на восприятие ветровых нагрузок // Металлические конструкции. Макеевка: Донбасская национальная академия строительства и архитектуры, 2018. 41–48.
- Корсаков А. Б., Щуров А. С. Расчет ветровых нагрузок на внешнюю поверхность вытяжной башни градирни методами вычислительной аэродинамики // Автоматизация и IT в энергетике. М.: Издательский дом «ИД АВИТ-ТЭК», 2015. 10–12.
- Корсун В. И., Стеблянко Л. В., Корсун А. В. Исследование напряженно-деформированного состояния железобетонной градирни // Вестник Донбасской национальной академии строительства и архитектуры. Макеевка: Донбасская национальная академия строительства и архитектуры, 2003. 113–118.
- Гмирач К. М., Козлов А. В., Проскуров Р. А. Подбор оптимальных параметров эллипсоидной железобетонной оболочки вращения // Международный научно-исследовательский журнал. — 2017. — № 2. — С. 100–104.







