При разработке залежей при больших градиентах давления на фильтрацию жидкости в пористой среде влияют инерционные силы, которые создают дополнительные сопротивления, направленные против движения.
Таким образом, при больших скоростях течения природа нелинейности закона фильтрации иная, чем при малых скоростях фильтрации. Когда течение достаточно медленное, соответственно медленно происходят деформации жидких частиц, и жидкость успевает реагировать на эти изменения. С увеличением скорости движения время прохождения через сужение уменьшается, и жидкие частицы не успевают деформироваться. Это приводит к увеличению сопротивления движения.
В статье предложено более общая формула, подобная формуле Дюпюи, которая учитывает также влияние инерционных сил и применима для произвольного полиномиального закона фильтрации.
Ключевые слова: скорость, инерционные силы, нелинейный закон, коэффициент продуктивности.
When developing deposits with large pressure gradients, the filtration of liquid in a porous medium is affected by inertial forces that create additional resistances directed against movement.
Thus, at high flow rates, the nature of the nonlinearity of the filtration law is different than at low filtration rates. When the flow is slow enough, the deformation of the liquid particles is slow, and the liquid has time to react to these changes. With increasing speed, the passage time through the narrowing decreases and the liquid particles do not have time to deform. This leads to an increase in traffic resistance.
The article proposes a more general formula similar to Dupuy's formula, which also takes into account the influence of inertial forces and is applicable to an arbitrary polynomial filtration law.
Key words: speed, inertia forces, nonlinear law, the coefficient of performance.
Основной задачей рациональной разработки нефтяных и газовых месторождений является полнота извлечения промышленных запасов нефти.
Наличие у жидкости релаксационных (неравновесных свойств) определяет характер сопротивления при движении в пористой среде. Течение через сужения и расширения поровых каналов сопровождается деформацией жидких частиц. Поскольку релаксирующая жидкость реагирует на изменение условий с некоторым запаздыванием, то в зависимости от скорости движения характер сопротивления будет меняться. 1,2.
В работе делается попытка обобщения закона фильтрации с учетом влияния инерционных сил при фильтрации нефти в пористой среде.
Следует отметить, что все процессы, которые искривляют диаграмму, увеличивают коэффициент а, b и наоборот.
Как известно, в 1901 году Форхгеймер, ссылаясь на исследования Мазони, рекомендовал выражать зависимость градиента давления от скорости (при больших градиентах) формулой: 
где а и b — эмпирические коэффициенты.
Будем считать это выражение моделью 1. Однако ученый отметил, что еще лучше зависимость 
от u будет выражаться трехчленным законом (модель 2): 
где с — эмпирический коэффициент.
Для проверки этого положения были обработаны индикаторные диаграммы некоторых скважин Уренгойского месторождения. Результаты обработки показали, что для прогноза модель 2 дает результаты значительно точнее, чем модель 1 1. В более общем случае закон фильтрации можно представить следующим образом:
. (1)
Здесь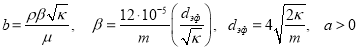 
.
Использование кубического слагаемого в уравнении
связано с необходимостью увеличения точности. Однако это необходимо также и для учета неравновесных свойств фильтрационного потока и влияния инерционных сил. Как видно, при 
из формулы (1) получается закон Дарси. А при а = 0 получается двучленный закон Форхгеймера. Подставляя в уравнение (1) 
, получаем:
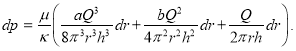
Интегрируя левую часть этого равенства от рс до рк, а правую часть 
, получим:
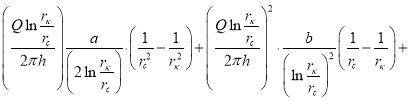
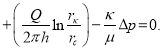Здесь 
Сделав подстановки
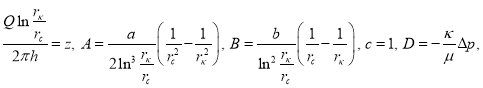
мы получаем кубическое уравнение в виде 
Для решения этого кубического уравнения используем подстановку 
Тогда данное кубическое уравнение представится в виде: 
Здесь 
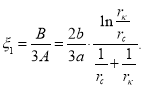
Для поставленной задачи 
и данное уравнение имеет всего один действительный корень, который можно найти по формуле Кардано.
Решение уравнения (1) по формуле Кардано имеет вид:
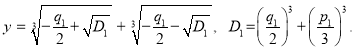
Последнее можно преобразовать в следующий вид:
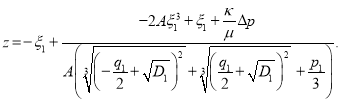
Делая подстановку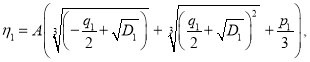 
мы получаем:
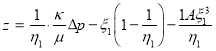. (3)
Здесь 
– безразмерный параметр, величина которого приблизительно равна единице 
Однако она — переменная величина. Учитывая в (3)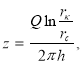 
мы получаем:
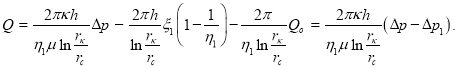(4)
Здесь 
(5)
Учитывая, что 
то из формулы (4) получается формула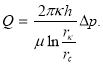 
Как видно из (5), градиент давления, который направлен против движения, состоит из двух составляющих. Первая 
, которая зависит от коэффициентов а, b и от характера изменения 
в процессе разработки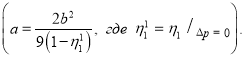 
А вторая составляющая учитывает влияние инерционных сил.
Графики изменения 
схематично имеют следующий вид:
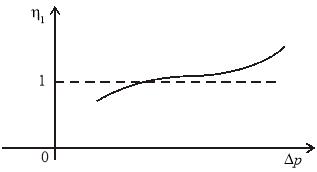
Рис.1. График изменения параметра
от депрессии 
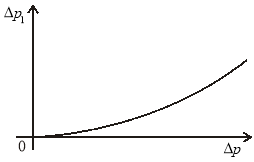
Рис.2. График изменения 
от депрессии 
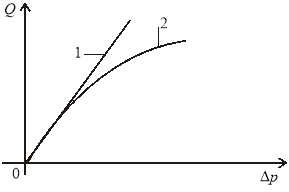
Рис. 3. График изменения
1 — по формуле Дюпюи; 2 — по формуле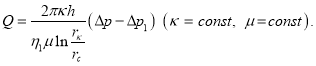 
Следует отметить, что полученные формулы можно применять не только для трехчленного закона фильтрации, но и для любого полиномиального закона фильтрации. Для этого в формулах (4) и (5) введем поправочную функцию 
, т. е. вместо 
возьмем выражение 
. Здесь коэффициент 
будет определяться с помощью данных полученных при гидрогазодинамических исследований скважин. Для этого проводится исследование методом установившихся отборов. По предложенной формуле (5) определяется 
. Далее по формуле
где для нефти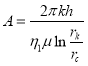 
, 
.
Таким образом, при различных 
определяется значение 
. Если 
то, 
, если же 
то 
. Тогда для его определения при различных 
используется формула 
. Полученные данные аппроксимируются по программе Excel [3]. Подставляя выражение для 
в формулах (4) и (5), мы получаем общие формулы для дебита флюида при нелинейном законе фильтрации для нефти:
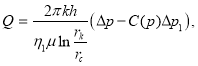(6)
где
или 
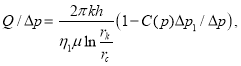(7)
Эта задача актуальна, потому что увеличение градиента, направленного против движения, отрицательно влияет на количество извлекаемых запасов. Со временем актуальность этой задачи будет увеличиваться в связи с тем, что открываемые новые месторождения находятся на все более больших глубинах. А с увеличением глубины увеличивается и скорость, и градиент давления. Поэтому увеличиваются и сопротивления, связанные с влиянием инерционных сил.
Таким образом, в статье получена более общая формула, учитывающая влияние инерционных сил и применима для произвольного полиномиального закона фильтрации.
Литература:
- А. Х. Мирзаджанзаде, О. Л. Кузнецов, Х. С. Басниев, З. С. Алиев. Основа технологии добычи газа. — М.: Недра, 2003, 880 с.
- А. Х. Мирзаджанзаде, И. М. Аметов, А. Г. Ковалев. Физика нефтяного и газового пласта. — Москва-Ижевск: Институт компьютерных исследований, 2005, 280 с.
- Спиридонов, О. В. Расширенные возможности Microsoft Excel 2003 / О. В. Спиридонов. — Центр дистанционных образовательных технологий МИЭМП, 2010.
