There are given the methods of proof using cubic polynome between the sides of triangle and its angles. On this occasion, we use theorem of Viet for main trigonometric functions and equation.
Key words: equation, triangle, inradius, radius of circumcircle, area, semiperimetr, theorem of Viet.
В данной статье описаны методы доказательства связи между углами и сторонами треугольника с использованием кубических полиномов. В этом случае мы использовали теорему Виета и основные тригонометрические функции.
Ключевые слова: уравнение, треугольник, радиус вписанной окружности, радиус описанной окружности, площадь, полупериметр, теорема Виета.
It is clear that we use different compound trigonometric expressions relating to the angles of triangle and the relations among the sides triangle for proving geometric inequality. For example, for interior angles ![]() of ABC triangle:
of ABC triangle:
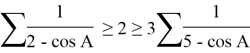
(According to the appearance, very “plain” inequality)
On this occasion the following method is really useful for us. Firstly,let’s get acquinted with simple lemma.
Lemma. The interior radius, half perimeter, ![]() sides and
sides and ![]() angles of ABC triangle are accordingly
angles of ABC triangle are accordingly ![]() va
va ![]() . In this case the following inequality is appropriate:
. In this case the following inequality is appropriate:

Proof. The following equation is not difficult to prove for any triangle:
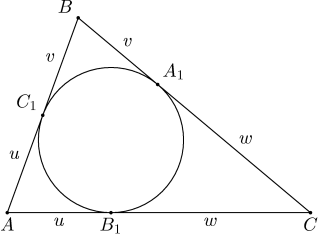

so, u=![]()
w=![]()
v=![]()
in this case, ![]()
![]()
![]()
From these inequalities ![]() can be seen easily.
can be seen easily.
From this
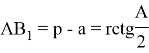
Lemma has been proved.
If we use ![]() in Lemma, we can have the following equation. Here R — externally drawn circle’s radius in the triangle.
in Lemma, we can have the following equation. Here R — externally drawn circle’s radius in the triangle.
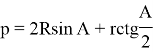
![]() (1)
(1)
We express ![]() va
va ![]() in the equality with the same trigonometric functions.
in the equality with the same trigonometric functions.
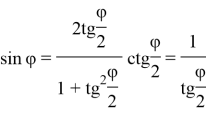
We tick as ![]() and bring it to (1) equation.
and bring it to (1) equation.
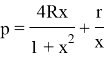
This equality expresses the equation in some ways. With simplifieng it, we have the following cubic equation:
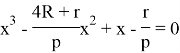
The roots of this equation are ![]()
If we use the theorem of Viyet for cubic equation,
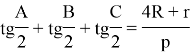
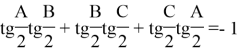
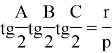
we have the above mentioned expressions. This is the first result, which was made via above mentioned first lemma.
Result 2. Now let’s tick as ![]() . From this
. From this
![]()

We bring these expressions to (1) equation.
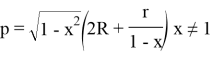
The equation is taken shape as following:
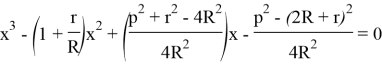
If we use the theoreme of Viyet for this equation,
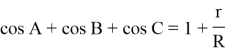
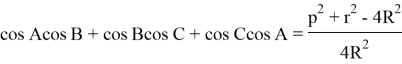
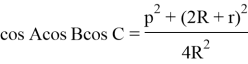
Result 3. The equation can be easily seen in the amount ![]() as following:
as following:
![]()
![]() triangle sides are the square rootsof this equation. If we use the theoreme of Viyet for the coefficient of the equation,
triangle sides are the square rootsof this equation. If we use the theoreme of Viyet for the coefficient of the equation,
![]()
![]()
Result 4. If ![]() va
va ![]() exchanges are accomplished in (1) equality, we can have the following equalities: (You can try this task)
exchanges are accomplished in (1) equality, we can have the following equalities: (You can try this task)
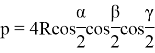
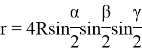
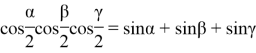
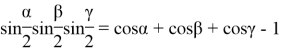
![]()
We direct the proof of the two above mentioned equality to the reader.
Proof: We divide the inequality into two parts.
Left side. According to Eyler inequality,
According to Gerretsion inequality, ![]()
We join them, ![]()
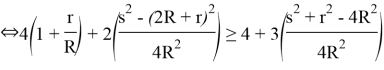
![]()
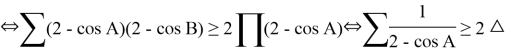
Right side.
According to Eyler inequality, ![]()
According to Gerretsion inequality, ![]() If we join them,
If we join them, ![]()
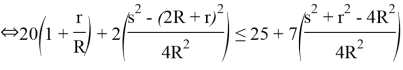
![]()
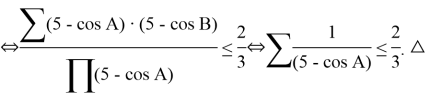
In addition, there are also inequalities, which are placed in the sides of triangle, namely contrast matter and they can be placed in the sides of triangle: For interior angles ![]() of ABC triangle:
of ABC triangle:
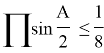
Proof. We use the following equation in order to prove the inequality:
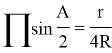
According to Eyler inequality, ![]() is clear. Therefore,
is clear. Therefore,
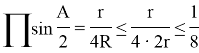
the inequality has been proved.
In conclusion we can tell that if we use different compound trigonometric expressions relating to angles of triangle, it will be so useful to prove many geometric inequations via above mentioned simple lemma.
References:
- Prosolov (Tasks for plantmeteres)
- Copyright 1996–2018 Alexandr Bogomolny
- Geometric inequalities marathon







