В данной статье представлен новый метод решения задачи Коши для линейного уравнения в частных производных первого порядка с постоянными коэффициентами, зависящего от двух переменных, и решение задачи Коши для уравнения продольных колебаний однородного стержня постоянного сечения методом понижения порядка.
Здесь и далее: ![]() ,
, ![]() — функции двух переменных,
— функции двух переменных, ![]() ,
, ![]() ,,
,, ![]() ,
, ![]() ,
, ![]() ,
, 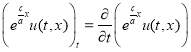 ,
, 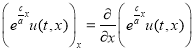 — частные производные, и вообще, для любой функции
— частные производные, и вообще, для любой функции ![]() будем полагать
будем полагать ![]() ,
, ![]() . Символ
. Символ ![]() будет означать, что из предыдущего уравнения получаем следующее.
будет означать, что из предыдущего уравнения получаем следующее.
1.Метод решения задачи Коши для линейного уравнения в частных производных первого порядка с постоянными коэффициентами, зависящего от двух переменных.
Данная задача Коши имеет вид [1]:
![]() ,
, ![]() ,
, ![]() , (1)
, (1)
![]() ,
, ![]() , (2)
, (2)
где ![]() — функция, имеющая первую производную,
— функция, имеющая первую производную, ![]() ,
, ![]() — вещественные числа, не равные нулю,
— вещественные числа, не равные нулю, ![]() — вещественное число.
— вещественное число.
Ход метода.
С одной стороны, из (1) следует
Умножим (3) на ![]() . Получим
. Получим
![]() . (4)
. (4)
Так как 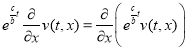 , и
, и 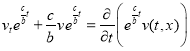 , то (4) можно представить в виде
, то (4) можно представить в виде
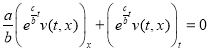 . (5)
. (5)
Положим в (5): ![]() .Тогда (5) будет иметь вид
.Тогда (5) будет иметь вид ![]() , или
, или
![]() . (6)
. (6)
Пусть ![]() — произвольное решение (6). Тогда, очевидно,
— произвольное решение (6). Тогда, очевидно, ![]() будет удовлетворять уравнению (1), то есть
будет удовлетворять уравнению (1), то есть
![]() . (7)
. (7)
С другой стороны, из (1) следует
![]() . (8)
. (8)
Умножим (8) на
![]() . (9)
. (9)
Так как 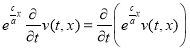 , и
, и 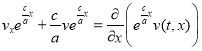 , то (9) можно представить в виде
, то (9) можно представить в виде
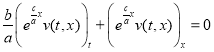 . (10)
. (10)
Положим в (10): ![]() .Тогда (10) будет иметь вид
.Тогда (10) будет иметь вид ![]() , или
, или
![]() . (11)
. (11)
Пусть ![]() — произвольное решение (11). Тогда, очевидно,
— произвольное решение (11). Тогда, очевидно, ![]() будет удовлетворять уравнению (1), то есть
будет удовлетворять уравнению (1), то есть
![]() . (12)
. (12)
Далее, поскольку уравнения (6) и (11) идентичны, то и их решение относительно ![]() , или
, или ![]() , будет одинаковым. Тогда, в данном случае, можно положить
, будет одинаковым. Тогда, в данном случае, можно положить
![]() . (13)
. (13)
Сопоставляя (7) и (12), с учетом (13), находим систему из двух уравнений:
![]() . (15)
. (15)
Приравнивая (14) и (15), находим, что в нашем случае будет выполнятся ![]() , откуда получаем равенство
, откуда получаем равенство ![]() , из которого следует
, из которого следует
![]() . (16)
. (16)
Очевидно, ![]() , где
, где ![]() – произвольная постоянная, будет решением уравнения (6), равно как и решением уравнения (11). В силу произвольности
– произвольная постоянная, будет решением уравнения (6), равно как и решением уравнения (11). В силу произвольности ![]() , можно положить
, можно положить ![]() , где
, где ![]() — произвольная дифференцируемая функция. Таким образом, имеем
— произвольная дифференцируемая функция. Таким образом, имеем
![]() . (17)
. (17)
В силу полученного равенства (16), в решении (17) можно заменить ![]() на
на ![]() , и решение (17) будет иметь вид
, и решение (17) будет иметь вид
![]() . (18)
. (18)
Поскольку функция ![]() — произвольная и дифференцируемая, то далее она может быть определена из условия (2). Подставим (18) в (7). Тогда получим
— произвольная и дифференцируемая, то далее она может быть определена из условия (2). Подставим (18) в (7). Тогда получим
![]() . (19)
. (19)
Применяя к (19) начальное условие (2), найдем окончательное решение задачи Коши (1), (2) в виде
2. Решение задачи Коши для уравнения продольных колебаний однородного стержня постоянного сечения методом понижения порядка.
Задача Коши для данного уравнения имеет вид [1], [2]:
![]() ,
, ![]() ,
, ![]() , (21)
, (21)
![]() ,
, ![]() , (22)
, (22)
![]() ,
, ![]() , (23)
, (23)
где для функций ![]() ,
, ![]() существует первая и вторая производная,
существует первая и вторая производная, ![]() — вещественное число, не равное нулю.
— вещественное число, не равное нулю.
Ход метода.
Уравнение (21) можно представить в виде ![]() , и далее, полагая функцию
, и далее, полагая функцию ![]() непрерывной по обеим переменным во всей области определения, в виде
непрерывной по обеим переменным во всей области определения, в виде ![]() , откуда далее, представим его в виде
, откуда далее, представим его в виде
![]() . (24)
. (24)
Положим в (24):
Тогда (24) будет иметь вид
![]() . (26)
. (26)
Уравнение (26) есть уравнение вида (1) при ![]() ,
, ![]() ,
, ![]() . Согласно формуле (19), его решением будет
. Согласно формуле (19), его решением будет
![]() , (27)
, (27)
где ![]() — произвольная функция, имеющая первую и вторую производную, далее подлежащая определению из начальных условий (22), (23). Подставляя найденное решение для
— произвольная функция, имеющая первую и вторую производную, далее подлежащая определению из начальных условий (22), (23). Подставляя найденное решение для ![]() из (27) в уравнение (25), находим, что решение уравнения (21) свелось к решению уравнения вида
из (27) в уравнение (25), находим, что решение уравнения (21) свелось к решению уравнения вида
![]() . (28)
. (28)
Таким образом, решение уравнения второго порядка (21) свелось к решению уравнения, подобного уравнению первого порядка вида (1), но с ненулевой правой частью. Далее выполним ряд следующих преобразований
![]() , (29)
, (29)
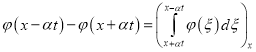 , (30)
, (30)
![]() . (31)
. (31)
Так как
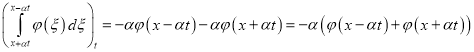 , (32)
, (32)
то подставляя (32) в (31) находим
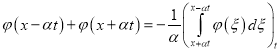 . (33)
. (33)
Подставляя (30) и (33) в (29) находим
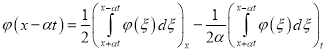 . (34)
. (34)
Далее, подставляя (34) в (28) находим
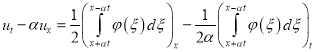 . (35)
. (35)
С уравнением (35) проведем следующие очевидные преобразования
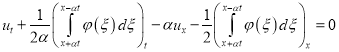 ,
, ![]()
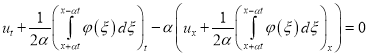 ,
, ![]()
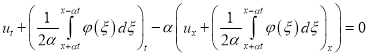 ,
,
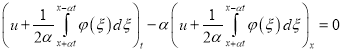 . (36)
. (36)
Уравнение (36) есть частный случай уравнения (1) при ![]() ,
, ![]() ,
, ![]() , если его рассматривать относительно функции
, если его рассматривать относительно функции 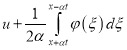 . Выполняя в уравнении (36) замену
. Выполняя в уравнении (36) замену
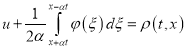 , (37)
, (37)
представим его в виде
![]() . (38)
. (38)
Исходя из решения (20) задачи Коши (1), (2), решение уравнения (38) имеет вид
![]() , (39)
, (39)
где ![]() — произвольная функция, имеющая первую и вторую производную, в дальнейшем подлежащая определению из начальных условий (22), (23). Таким образом, приравнивая (37) и (39) находим, что
— произвольная функция, имеющая первую и вторую производную, в дальнейшем подлежащая определению из начальных условий (22), (23). Таким образом, приравнивая (37) и (39) находим, что
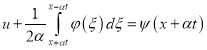 . (40)
. (40)
Очевидно, что уравнение (21) будет равносильно уравнению ![]() , и проведя аналогичные рассуждения, заменив
, и проведя аналогичные рассуждения, заменив ![]() на
на ![]() , получим еще одно решение, подобное (40):
, получим еще одно решение, подобное (40):
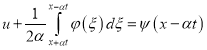 , (41)
, (41)
так как интеграл слева в (40), при замене ![]() на
на ![]() , остается прежним. Складывая (40) и (41), получим
, остается прежним. Складывая (40) и (41), получим
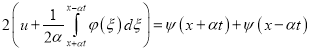 . (42)
. (42)
Из (42) элементарными преобразованиями получаем
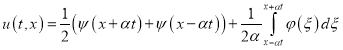 . (43)
. (43)
Применяя начальные условия (22), (23) к решению (43), найдем окончательное решение задачи Коши (21)-(23) в виде
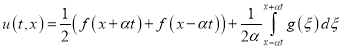 .
.
Литература:
- С. Фарлоу. Уравнения с частными производными для научных работников и инженеров,издательство «Высшая школа», Москва, (1985) — 384 с.
2. Н. С. Кошляков, Э. Б. Глинер, М. М. Смирнов. Уравнения в частных производных математической физики, издательство «Высшая школа», Москва, (1970) — 712 с.







