В статье представлена процесс разработки пользовательского приложения, решающего задачу поиска максимального потока алгоритмами Форда-Фалкерсона и Эдмонса-Карпа.
Ключевые слова: теория графов, задача поиска максимального потока, разработка приложений.
Теория графов универсальный инструмент, на основе которого могут решаться различные задачи, в том числе задачи поиска наилучшего с какой-либо точки зрения распределения узлов и дуг для получения или максимального «выигрыша» или минимального «проигрыша». Алгоритмы экстремальных задач на графах фактически являются одним из инструментов системного анализа.
Теория графов работает с довольно большим объемом данных. Алгоритмы, непосредственно обрабатывающие эти данные, также являются довольно громоздкими, так как представляют из себя последовательность действий, где текущий шаг необязательно зависит от предыдущего. Следствием этого является невозможность быстро определить, привело ли решение к верному ответу или нет, и на какой итерации была совершена ошибка.
Исходя из этих предпосылок, была поставлена цель: разработать программный продукт, который будет решать задачу о нахождении максимального потока. При этом полезно предусмотреть возможность вывода промежуточного решения, полученного на i-той итераций алгоритма. Программа должна работать с достаточно большим объемом информации, обрабатывать его в минимальный промежуток времени, иметь интерфейс, который был бы интуитивно понятен пользователю и прост в использовании.
Продукт реализует на платформе Microsoft Visual Studio 2019 (языки разработки C++ и C#) алгоритмы Форда-Фалкерсона и Эдмонса-Карпа, решающие задачу поиска максимального потока. Так как целью работы являлась разработка интерфейсного приложения, то для комфортной работы пользователя будет предлагаться несколько способов ввода данных. Вывод данных производится на интерфейс, с соответствующими пояснениями. В продукте также возможен вывод промежуточного значения ни i-той итерации алгоритма, а так же очищение всех полей ввода данных.
Для реализации были выбраны следующие алгоритмы.
Алгоритм Форда-Фалкерсона является одним из самых распространенных алгоритмов решения задачи нахождения максимально потока в транспортной сети. Алгоритм имеет непосредственную связь с теоремой Форда-Фалкерсона: для любой сети с одним источником и одним стоком величина максимального потока в сети от источника к стоку равна величине пропускной способности (минимального разреза).
Алгоритм Форда-Фалкерсона основан на следующих теориях:
-
Предположим, что в сети имеется некоторый поток и путь из s в t, состоящий из ненасыщенных дуг (дуга является ненасыщенной, когда пропускная способность не равна (меньше) потока по сети). Очевидным будет то, что поток в сети можно увеличить на величину
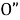 , минимальную из остаточных пропускных способностей дуг, входящих в этот путь. Перебирая все возможные пути из s в t и проводя процедуру увеличения потока, пока это возможно, получим в результате полный поток, то есть такой поток, для которого поток из s в t содержит по крайней мере одну насыщенную дугу.
, минимальную из остаточных пропускных способностей дуг, входящих в этот путь. Перебирая все возможные пути из s в t и проводя процедуру увеличения потока, пока это возможно, получим в результате полный поток, то есть такой поток, для которого поток из s в t содержит по крайней мере одну насыщенную дугу.
Рассмотрим произвольный маршрут из s в t. Дуги, образующие этот маршрут, естественным образом делятся на прямые (от s в t) и обратные (от t в s). Пусть существует путь, в котором прямые дуги не насыщены, а потоки в обратных дугах положительны. Пусть ![]() — минимальная из остаточных пропускных способностей прямых дуг, а
— минимальная из остаточных пропускных способностей прямых дуг, а ![]() — минимальная их величин потоков обратных дуг. Тогда поток в сети можно увеличить на величину
— минимальная их величин потоков обратных дуг. Тогда поток в сети можно увеличить на величину ![]() , прибавляя
, прибавляя ![]() к потокам на прямых дугах и вычитая
к потокам на прямых дугах и вычитая ![]() из потоков на обратных дугах.
из потоков на обратных дугах.
Очевидно, что при этом условие сохранения потока
![]()
для узлов, входящих в рассматриваемый маршрут, не нарушится. Если множество обратных дуг не пусто, то при такой процедуре увеличения потока в сети фактического перемещения объектов вдоль рассматриваемого маршрута не происходит, так как оно в принципе невозможно. Однако эта процедура уменьшает потоки на некоторых дугах, которые, возможно, были перед этим насыщенными, образуя таким образом новые пути из ненасыщенных дуг, вдоль которых и происходит фактические перемещения потока величины ![]() . Ясно также, что первая процедура является частным случаем второй.
. Ясно также, что первая процедура является частным случаем второй.
Получена авторская программная реализация алгоритма:
onEnd [EdgCount] = v;
nextEdg [EdgCount] = firstEdg [u];
firstEdg [u] = EdgCount; // началом списка становится новое ребро
capacity [EdgCount++] = cap; // определяем пропускную способность
// Обратное ребро
onEnd [EdgCount] = u; // на конце обратного u
nextEdg [EdgCount] = firstEdg [v];// добавляем в начало списка для v
firstEdg [v] = EdgCount;// началом списка становится новое ребро
capacity [EdgCount++] = 0; }// определяем пропускную способность
int findFlow (int u, int flow) {
if (u == destinationVertex) return flow; // возвращаем полученный минимум
visited [u] = true;
for (int Edg = firstEdg [u]; Edg!= — 1; Edg = nextEdg [Edg]) {int to = onEnd [Edg];
if (!onEnd [Edg & & firstEdg [u] > > 0) {
// ищем поток в поддереве
int minResult = findFlow(to, min(flow, capacity [Edg]));
if (minResult > 0) {
capacity [Edg] -= minResult;
capacity [Edg ^ 1] += minResult; }}}
return 0;}
int main() {
fill(firstEdg, firstEdg + MAX_V, -1);// определяем существование ребра
cin >> numOfVertex >> numOfEdg;//считываем количество вершин и ребер
cin >> sourceVertex >> destinationVertex; // считываем источник и сток
for (int i = 0, u, v, cap; i) { cin >>> u >>>>>>> v >>>>>>>>>>> крышка; addEdg(u, v, cap); }
// Нахождение максимального потока
int maxFlow = 0;
int iterationResultt = 0;
while ((iterationResultt t = findFlow(sourceVertexx, INF)) > 0) { fill(visited, visited + MAX_V, false);
maxFlow + = iterationResultt;}
Алгоритм Эдмондса–Карпа является более углубленной реализацией метода Форда–Фалкерсона, в которой в качестве дополняющего пути выбирается кратчайший по рёбрам путь в остаточной сети (длины всех рёбер равны 1).
Остаточная пропускная способность пропускная способность ребра за вычетом текущего потока вдоль этого ребра. При этом если некоторый поток протекает по ориентированному ребру, то возникает так называемое обратное ребро (направленное в обратную сторону), которое будет иметь нулевую пропускную способность, и по которому будет протекать тот же по величине поток, но со знаком минус. Если же ребро было неориентированным, то оно как бы распадается на два ориентированных ребра с одинаковой пропускной способностью, и каждое из этих рёбер является обратным для другого (если по одному протекает поток F, то по другому протекает –F).
Общая схема алгоритма Эдмондса-Карпа такова. Полагаем поток равным нулю. Затем ищем дополняющий путь, т. е. простой путь из s в t по тем рёбрам, у которых остаточная пропускная способность строго положительна. Если дополняющий путь был найден, то производится увеличение текущего потока вдоль этого пути. Если же пути не было найдено, то текущий поток является максимальным. Для поиска дополняющего пути могут использоваться обход в ширину и обход в глубину.
Рассмотрим подробнее процедуру увеличения потока. Пусть мы нашли некоторый дополняющий путь, тогда пусть c наименьшая из остаточных пропускных способностей рёбер этого пути. Процедура увеличения потока заключается в следующем: для каждого ребра (u, v) дополняющего пути выполним: F(u, v) += C, а F(v, u) = F(– u, v) (или, что то же самое, F(v, u) –= C).
Величиной потока будет сумма всех неотрицательных величин F(S, v), где v любая вершина, соединённая с истоком.
Полученная авторская программная реализация алгоритма:
//найти путь приращения в остаточном графе
bool path(int u, int v)
{ queue
int C, F;
for(int i = 0; i < n; i++) p [i] = -1;
O.push(u);
p [u] = u;
while(!O.empty())
{ x = O.front(), O.pop();
if(x == v) return true;
for(int i=last [x]; i!= — 1; i=prev [i])
{ y = to [i];
F = f [i];
C = c [i];
if(p [y] == -1 && C > F)
{ p [y] = x;
Edg [y] = i;
O.push(y); }}}
return false;}
// увеличение потока
int send(int u, int v)
{ bottleneck = INF;
int x, y, index, sym;
y = v;
while(p [y]!= y)
{ x = p [y];
index = Edg [y];
bottleneck = (bottleneck > c [index]-f [index]? c [index]-f [index]: bottleneck);
y = x;} }
y = v;
while(p [y]!= y)
{ x = p [y];
index = Edg [y];
f [index] += bottleneck;
f [index^ 1] -= bottleneck;
y = x; }
return bottleneck;}
Перечислим основные процедуры и функции, реализующие работу приложения:
function FF(Mass:Matrix); функция, решающая задачу алгоритмом Форда-Фалкерсона.
function EK(Mass:Matrix); функция, решающая задачу алгоритмом Эдмонса–Карпа.
Function List(); функция, очищающая поля ввода данных на интерфейсе.
Function RItt(i:Integer); функция возвращающая промежуточные данные по алгоритму.
Function Iflag(flag:Integer); функция отображающая кнопку «Пуск» на форме.
Возвращаемые значения:
RVes; максимальная величина потока.
RMass; ребра, образующие разрез минимальной пропускной способности.
RReb; количество итераций алгоритма.
delta; величина, на которую увеличивается поток в сети.
RReb; список вершин.
Разработанный пользовательский интерфейс выглядит следующим образом:
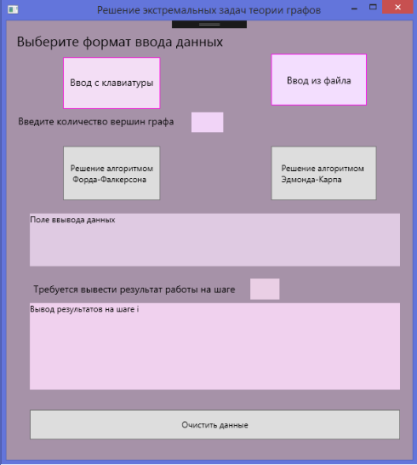
Рис. 1. Главное окно программы
Данные загрузим в программу из текстового файла *.txt. Алгоритм представленный в тестировании — Алгоритм Форда-Фалкерсона.

Рис. 2. Пример работы
В процессе работы была реализована программа, имеющая пользовательский интерфейс и работающая с алгоритмами, решающими задачу нахождения максимального потока графа.
На стадии разработки и отладки были обнаружены и решены следующие проблемы:
- Проверка на корректность вводимых параметров.
Количество вершин в графе число целое и ограничено размерностью 100. Данное условие не является жестким, и ограничивает пространство решаемых задач в связи с временем отработки алгоритмов. Также рекомендуется для графов с количеством вершин более 20 использовать ввод данных из текстового файла.
- Оптимизация интерфейса.
Для комфортности пользовательского интерфейса и чтобы избежать перегрузки формы различными объектами, сбивающими пользователя, было реализовано следующее решение. Кнопка для вывода данных на какой-либо итерации алгоритма появляется на форме только после отработки выбранного алгоритма. Для этого в тексте кода реализован флаг, делающий данную опцию доступной.
- Перенос разработанных программ в полноценное интерфейсное приложение.
Реализация алгоритмов для данного продукта была произведена ранее на языке C++. Поскольку и язык C++ и язык С# относятся к Си-подобным языкам, первоначально считалось, что интеграция произойдет легко и безболезненно. Однако возникли следующие проблемы: передача данных с клавиатуры требовала отдельного внимания в связи с особенностями объекта «TextBlock». Также было решено добавить возможность очищения всех полей, доступных для ввода.
Чтобы использовать данную программу, необходимы следующие вычислительные ресурсы ПК:
– процессор: Pentium x86 и выше,
– видеокарта: любая с видеопамятью от 16Мб,
– минимальный объем ОЗУ: 128Мб, рекомендуется 256Мб и выше,
– жесткий диск: программа занимает около 5Мб на жестком диске,
– ОС: Windows 7 и выше,
– мышь и клавиатура.
Продукт прошел стадии разработки, отладки, тестирования и готов к стадии production. Рекомендуется к использованию для самообучения и самопроверки знаний студентов учебных заведений.







