Область досягаемости в задаче о свободном движении тела в поле тяготения Земли



В работе рассматривается простое решение задачи определения характеристик траектории тела, брошенного под углом к горизонту с заданной высоты, без учёта сопротивления среды. Вводится понятие области досягаемости как совокупности точек пространства, которые могут быть достигнуты при всех возможных углах бросания, и определяются её границы.

Ключевые слова: свободное падение, характеристики траектории движения тела, брошенного под углом к горизонту, область досягаемости.

Задача о свободном падении тела вблизи поверхности Земли изучена довольно основательно. Это движение в вакууме описано, например, в [1–4]. Традиционно при рассмотрении этой темы в школе основное внимание уделяется проблемам определения вида траектории движения, расчёта дальности полёта, получения аналитического выражения для необходимого угла бросания. При этом, к сожалению, не рассматривается проблема определения той области в плоскости движения тела, которая содержала бы в себе все точки пространства, которые могут быть достигнуты в процессе свободного движения тела, брошенного под различными углами к горизонту при заданной начальной высоте и известной начальной скорости.

Решение этой актуальной задачи представляет интерес как учебно-методический при изучении темы в школе, так, возможно, и практический при предварительной оценке тактико-технических характеристик артиллерийских систем и стрелкового оружия.

1. Уравнение траектории в относительных переменных

Траектория движения изображена на рис. 1, где x и y — соответственно, горизонтальная и вертикальная координаты тела, v₀ — начальная скорость, h — начальная высота, α — угол бросания, D — дальность полёта.

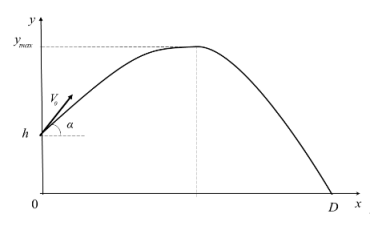
Рис. 1. Схема движения

В [1–4] для этой траектории получено следующее уравнение:

y = h + tg α ּ x — (1 + tg² α ּ) x². (1)

Для упрощения последующего анализа перейдём в этом выражении к безразмерным относительным величинам с помощью следующих обозначений [3]:

= H, = X, = Y, = a.

Физический смысл нормирующего множителя H состоит в том, что его значение равно максимальной высоте подъёма y_max при начальной скорости v₀, направленной вертикально вверх (при h = 0 и α = ). В безразмерных величинах X и Y уравнение траектории (1) принимает вид [3]:

Y = a + tg α ּ X — (1 + tg² α) ּ .

Оно упрощается, если обозначить tg α = z:

Y = — (1 + ) ּ + z ּ X + a. (2)

Уравнение (2) является квадратным как относительно горизонтальной координаты X, так и относительно тангенса угла бросания z. Целесообразно в (2) сделать замену переменной = s, чтобы получить уравнение траектории в виде

Y = ּ + ּ X + a, (3)

обеспечивающем затем в пунктах 4 и 5 довольно простое определение максимальной дальности полёта.

2. Геометрическое место вершин траекторий

Выражение (2) представляет собой уравнение параболы, известное из школьного курса математики как y=a+ bx + c. Также из программы по математике известно, как можно найти координаты и вершины параболы: = , = y (). Воспользуемся этими простыми формулами для того, чтобы найти координаты X_В и Y_В вершин парабол, определяемых уравнением (2). Получим:

X_в = 2. (4)

Подставив это выражение в (2), получаем значение ординаты вершины параболы:

Y_в = + a. (5)

Пара выражений (4) и (5) представляет собой в неявном виде уравнение той линии, на которой находятсявсевершины парабол — высшие точки всевозможных траекторий. Эта линия схематически изображена на рис. 2.

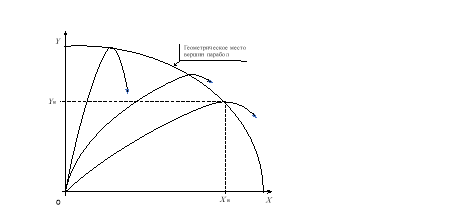
Рис. 2. Схема геометрического места вершин траекторий

Уравнение (4) — (5) получено в параметрической форме, в качестве параметра в нём выступает величина z. Желательно получить это уравнение в явном виде, а для этого из выражений (4) и (5) нужно исключить параметрz. Удобно сделать это, если из (5) выразить как функцию от Y_в и подставить его в (4). Но в (4), кроме , есть ещё и z в первой степени, поэтому, чтобы не вводить в преобразования квадратный корень, вначале возведём в квадрат левую и правую части равенства (4). После несложных преобразований получаем уравнение геометрического места вершин траекторий уже в явном виде:

+ (1 + 2a) Y_в + a + a² = 0. (6)

Геометрическим образом уравнения (6) является эллипс, показанный на рис. 3 для случая нулевой начальной высоты (h = 0).

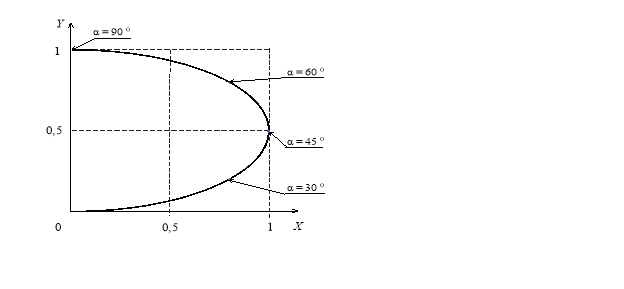
Рис. 3. Геометрическое место вершин траекторий в координатах X и Y при h = 0

При изменении начальной высоты h эллипс, изображённый на рис. 3, перемещается по оси ординат на величину , причём при положительном значении h — вверх, а при отрицательном — вниз.

Уравнение эллипса (6) можно привести к более простому виду, если выполнить масштабирование по оси X, то есть если перейти к новой переменной X1 по правилу X1 = 0,5 Xв. В получившемся уравнении в переменных X1 и Yв можно выделить полный квадрат и получить окончательно:

X1² + (Yв — (0,5 + a))² = 0,5². (7)

Из школьного курса математики известно, что (7) — это уравнение окружности с центром в точке (0,5; 0,5 + a) и радиусом, равным 0,5.

Таким образом, в координатах X1 и Yв вершины траекторий находятся на полуокружности с радиусом, равным 0,5, и центром, находящимся на оси ординат в точке 0,5 + a (рис. 4).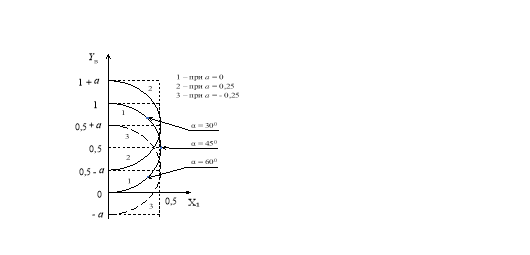

Рис. 4. Полуокружности вершин траекторий (1 — при a = 0; 2 — при a = 0,25; 3 — при a = — 0,25)

Линия 1 на рис. 4 соответствует нулевому значению начальной высоты (h = 0). Из выражения (7) следует, что изменение начальной высоты h приводит только к перемещению центра окружности по оси ординат на величину , причём при положительном значении h — вверх (окружность 2 на рис. 4), а при отрицательном — вниз (окружность 3 на рис. 4). Величина радиуса полуокружности (0,5) при изменении начальной высоты не изменяется.

Для случая нулевой начальной высоты на рис. 4 отмечены также точки, соответствующие углам бросания α, равным 30⁰, 45⁰ и 60⁰. Из рисунка 4 видно, что нижняя часть полуокружности соответствует настильным (невысоким) траекториям, при которых α<45⁰, а верхняя часть — навесным (высоким) траекториям, для которых α >45⁰.

Поскольку вершины парабол являются самыми верхними точками траекторий движения, вполне естественным было бы предположить, что при X ≤ 1 верхняя часть полуокружностей, изображённых на рисунке 4, и является верхней границей для искомой области досягаемости. Однако в пункт 6.1 мы покажем, что это не так.

Ещё одной характеристикой, определяющей размер искомой области досягаемости в другом направлении — в горизонтальном, является дальность полёта. Поэтому далее в пунктах 4 и 5 получим явные выражения для дальности полёта в зависимости от величины угла бросания (α), выясним ограничения на α и a, а также исследуем зависимость максимальной дальности полёта и угла, обеспечивающего максимальную дальность, от начальной высоты (как положительной, так и отрицательной).

3. Дальность полёта

Из выражения (3) при Y = 0, то есть при падении тела на землю, получаем:

4 d — 4 s a = 0. (8)

Здесь через d обозначено значение безразмерной горизонтальной координаты X при Y = 0: d = . Решив относительно переменной d квадратное уравнение (8), получаем значение дальности полёта:

d = 2 ( + ). (9)

Важно отметить, что это выражение — алгебраическое и получено оно — в отличие от аналогичного выражения (10) в работе [3] — без привлечения тригонометрических формул, которые к моменту изучения школьниками темы «Движение тела, брошенного под углом к горизонту» освоены ими ещё не достаточно полно. При этом в выражении (9) нет знаменателя и в нём не три корня, как в выражении (15) работы [3], а только два. Это значительно упрощает в дальнейшем вычисление производной от дальности d.

Из выражения (9) видно, что дальность полёта зависит от величины s (от угла бросания) и от начальной высоты (a). Эту зависимость и будем анализировать далее. При этом начальная высота (a) и угол бросания (α) не могут быть произвольными. Из (9) следует, что подкоренное выражение в нём должно быть неотрицательным, то есть a ≥ s . Соответствующая область допустимых значений a и s показана на рисунке 5 в виде заштрихованной зоны.

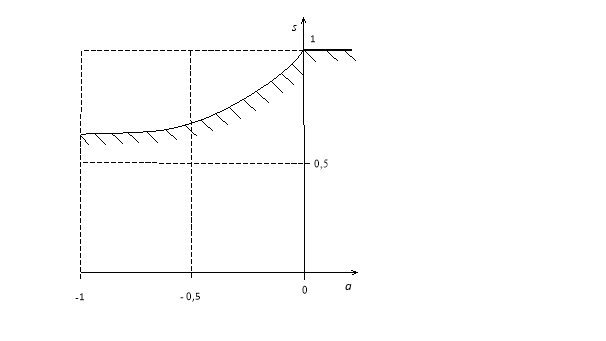
Рис. 5. Область допустимых значений для a и s

4. Максимальная дальность полёта

Из выражения (9) следует, что при нулевой начальной высоте (a = 0) дальность полёта определяется выражением d (a = 0) = 4, то есть зависит только от величины угла бросания (α). Эту зависимость можно представить в виде d (a = 0) = 2 sin (2 α), из чего следует известный вывод, что при нулевой начальной высоте максимальная дальность (d_m), равная двум, достигается при угле бросания α, равном 45⁰. Однако при начальной высоте h, отличной от нуля, величина максимальной дальности уже зависит от высоты старта, а необходимый угол бросания отличается от 45⁰ и определяется параметром a. В статье [3, с. 35] утверждается, что угол α_m, обеспечивающий максимальную дальность полёта, не превышает 45⁰. Далее мы докажем, что этот угол может быть как меньше, так и больше, чем 45⁰, в зависимости от начальной высоты. Для этого рассмотрим в выражении (9) дальность полёта d как функцию независимой переменной s, считая при этом переменную a параметром задачи.

Для определения экстремума функции d (s) записываем производную d по s (для этого необходимо знать формулу производной только от степенной функции) и приравниваем её нулю:

= .

После возведения в квадрат левой и правой частей этого равенства получаем для переменной s, обеспечивающей максимальную дальность d_m, следующее выражение:

s_m = . (10)

Если теперь с помощью замен переменных вернуться к исходной переменной α, то для угла бросания α_m, обеспечивающего максимальную дальность полёта, получаем его явное выражение в зависимости от безразмерной начальной высоты (a):

sin α_m = . (11)

Графически зависимость (11) представлена на рисунке 6.

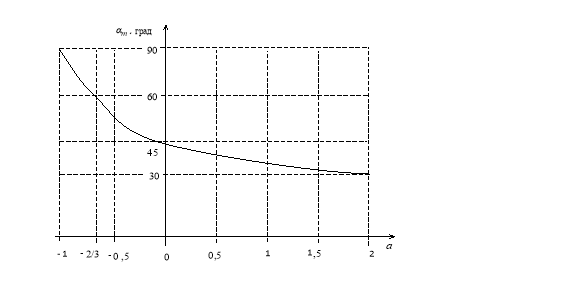
Рис. 6. Угол бросания (α_m), обеспечивающий максимальную дальность, в зависимости от начальной высоты a

Из рисунка 6 и из выражения (11) видно, что в зависимости от начальной высоты угол α_m, обеспечивающий максимальную дальность d_m, может быть как меньше, так и больше, чем 45⁰.

Теперь, имея явное выражение для угла бросания, который обеспечивает максимальную дальность, получим явное выражение и для самой максимальной дальности d_m в зависимости от начальной высоты. Для этого подставим s_m из (10) в (9) вместо s и получим:

d_m = 2. (12)

Графически эта зависимость показана на рисунке 7.

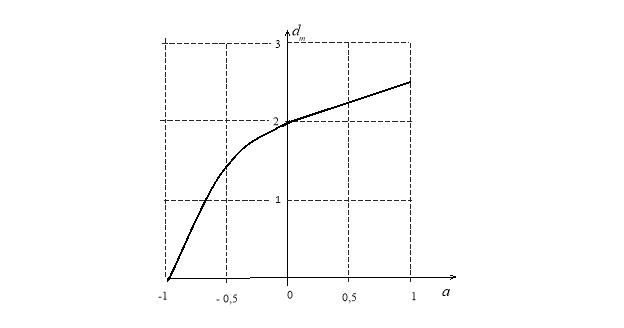
Рис. 7. Максимальная дальность (d_m) в зависимости от начальной высоты a

При произвольной начальной высоте (a) выражение (12) определяет крайнюю точку на оси X для области досягаемости.

Отметим, что выражение (12) для максимальной дальности полёта d_m фактически совпадает с аналогичным выражением (12), приведённым в работе [4] в других переменных, но получено оно проще, чем в [4], поскольку для этого не использовались тригонометрические формулы.

Отметим также, что выражения (10) и (12) получены нами выше с помощью хоть и простого, но всё же дифференцирования, которое школьниками в момент изучения ими темы «Баллистическое движение» ещё не знакомо. Поэтому желательно попытаться получить те же выражения, но не используя для этого производные. Далее покажем, что это действительно возможно. Для этого, обозначив в выражении (9) 1 — s = u, запишем его в виде

d(u) = 2 ( + ).

Возведём его левую и правую части в квадрат, чтобы остался только один корень:

= 8 (1 — u) (u + ) + ).

Разделив на 8, получаем функцию, график которой уже можно построить. Например, при a = 0,2 и a = 0,5 можно убедиться в том, что максимального значения эта функция достигает при значениях u, равных . А тогда из замены переменной 1 — s_m = u_m находим, что s_m = . Это значение совпадает со значением (10), полученным выше с использованием производной. А это и доказывает, что справедливость формул (11) и (12), по которым определяется максимальная дальность полёта, можно установить и без привлечения для этого производных.

5. Область досягаемости

5.1. Из изложенного в пунктах 3–5 следует, что при a = 0 искомой области досягаемости принадлежат следующие две подобласти в системе отсчёта XOY (рис. 8):

– подобласть 1, находящаяся под дугой эллипса между точками (0; 1) и (1; 0,5),

– подобласть 2 под параболой, соответствующей углу α в 45⁰, между точками (1; 0,5) и (2; 0).

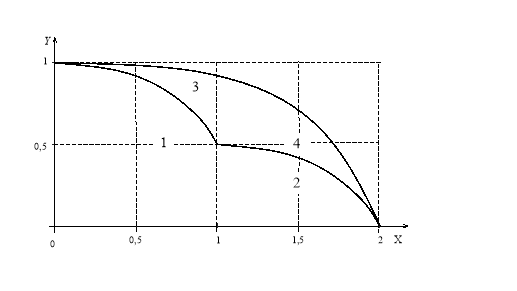
Рис. 8. Область досягаемости

5.2. Докажем, что над подобластью 1 есть некоторая подобласть области досягаемости. Ординаты траекторий (Y) определяются выражением (2), а ординаты вершин парабол (Yв) — выражением

Yв = (),

которое получаем при 0≤ X≤1 в результате решения квадратного уравнения (6) относительно Yв. Запишем разность этих ординат:

R1 = Y — Yв = — (1 + ) X² + zX — (1 + ).

Эта разность не зависит от начальной высоты a, а зависит только от X и z. Для того чтобы доказать, что над подобластью 1 существует и ещё одна подобласть значений X и Y, достаточно указать хотя бы одну пару чисел X и z, при которых разность R1 положительна. Разность R1 больше нуля, например, при X = 0,9 и z = 2, а это и доказывает, что над подобластью 1 при 0≤ X≤1 есть и ещё одна подобласть (назовём её подобластью 3 — рис. 8) достижимых точек в плоскости XOY.

1. Докажем, что и над подобластью 2 находится некоторая подобласть области досягаемости.

Ордината Yп траектории, соответствующей углу бросания в 45⁰, определяется выражением

Yп = — X² + X. (13)

Запишем разность ординат траекторий, определяемых выражениями (2) и (13) и, поскольку для дальнейшего важен только знак этой разности, умножим её на . Тогда при a = 0 и 1X≤2 получим: R2 = 4 — (1 + z) X. Графически зависимость R₂ от X представлена на рисунке 9.

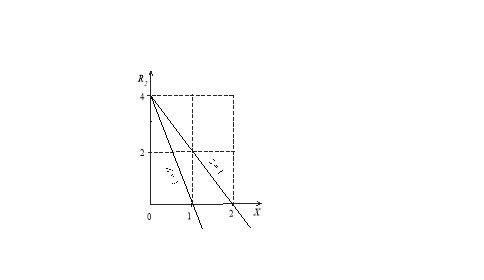
Рис. 9. Разность ординат (R₂) в зависимости от X

Из рисунка 9 видно, что при 1<z<3 разность R2 положительна. Следовательно, ординаты траекторий выше, чем парабола, соответствующая углу в 45⁰, причём при увеличении X от 1 до 2 размер подобласти 4 уменьшается до нуля (рис. 8).

Таким образом, область досягаемости представляет собой сумму (объединение) четырёх подобластей (рис. 8), и теперь необходимо найти верхнюю границу этой области.

2. Верхняя граница области досягаемости

Получим аналитическое выражение для верхней границы области досягаемости. Для этого выражение (2) представим как уравнение параболы относительно переменной z:

Y = — + ּX z — X² + a. (14)

Из школьного курса алгебры известно, что наибольшее значение параболы y=a+ bx + c достигается при x = . Воспользовавшись этим простым правилом, найдём для каждого из значений X то значение переменной z, при котором получается максимальное значение для Y: z = . Подставив это значение в (14), получаем:

Y = 1–0,25 X² + a.

Это и есть уравнение верхней границы области досягаемости. Эта линия ограничивает область досягаемости сверху. Слева и снизу при нулевой начальной высоте эта область ограничена, соответственно, осью ординат и осью абсцисс. При изменении начальной высоты верхняя граница области досягаемости перемещается по оси Y на величину, равную a, причём при положительных значениях a — вверх, а при отрицательных — вниз.

6. Заключение

Предложено простое, доступное учащимся среднего уровня подготовленности, решение задачи анализа свободного движения тела, брошенного под углом к горизонту. Упрощение анализа особенностей задачи достигнуто в результате того, что всё исследование выполнено в безразмерных относительных величинах, а также вследствие перехода к переменным, в которых уравнения имеют более простой вид. При этом удалось обойтись практически без тригонометрических формул, которые к моменту изучения школьниками темы «Движение тела, брошенного под углом к горизонту» освоены ими ещё не в полной мере, а также без нахождения производных от сложных функций.

Введено понятие области досягаемости как множества точек в плоскости движения, которые могут быть достигнуты при заданной начальной скорости, известной начальной высоте и всевозможных углах бросания. Определены границы области досягаемости.

Изложение материала, приведённое в этой работе, может быть полезным как учащимся, так и преподавателям физики в школе.

Следуя одному из основных дидактических принципов образования — доступность и преемственность с тем содержанием, которое осваивается в школе [5, с. 59], — анализ задачи, представленный в настоящей статье, рассчитан на учащихся с базовым уровнем знаний по физике и математике. Поэтому этот анализ основывается исключительно на средствах и приёмах, доступных этой категории учащихся, и тем самым он предоставляет всем школьникам равные возможности для решения ими творческих задач.

Литература:

1. Касьянов В. А. Физика. 10 класс. Профильный уровень. — М.: Дрофа, 2013–428 с.
2. М. М. Балашов, А. И. Гомонова, А. Б. Долицкий и др. Физика: Механика. 10 класс: Учебник для углублённого изучения физики/ Под ред. Г. Я. Мякишева. — М.: Дрофа, 2004–496 с.
3. Бобылев Ю. В., Грибков А. И., Романов Р. В. «Кидай дальше», или Четыре способа решения одной известной физической задачи/ Физика в школе — 2018 — № 3 — С. 33–38.
4. Бобылев Ю. В., Грибков А. И., Романов Р. В. Нестандартное нахождение траектории тела при свободном падении и её анализ/ Физика в школе — 2019 — № 2 — С. 31–35.
5. Казакова Ю. В., Петрова Е. В. Размышления учителя физики о состоянии и перспективах развития исследовательской деятельности учащихся/ Физика в школе — 2015 — № 1 — С. 53–60.