Геометрический материал как средство формирования логического мышления младших школьников в условиях реализации ФГОС НОО



Обучение в школе направлено не только на формирование у учащихся знаний, умений и навыков, но и на развитие школьников. Одной из задач начальной школы, которая определена законодательством и зафиксирована в Федеральном государственном образовательном стандарте второго поколения, является создание условий для овладения учащимися элементами логических действий и операций (сравнение, анализ, синтез, обобщение, классификация и т. д.). Развитие логического мышления протекает в несколько этапов, один из которых приходится именно на младший школьный возраст. Поэтому перед учителем стоит задача развивать у школьника самостоятельную логику мышления, позволяющую ему продуцировать умозаключения, доказывать свою точку зрения, используя доказательства и логически связанные между собой высказывания, обращаться к определенным истокам знаний сознательно и по собственной инициативе.

Проблемами мышления детей младшего школьного возраста занимались многие зарубежные и отечественные психологи: Ж. Пиаже [13], Л. С. Выготский [1], С. Л. Рубинштейн [14], А. Н. Леонтьев [3], П. Я. Гальперин [2], Н. В. Талызина [15] и др.

Большое значение в развитии логического мышления младшего школьника отводится математике. Эта наука отличается высоким уровнем абстракции и переходом в воспроизведении знаний от абстрактного к конкретному. Именно задания геометрического характера отвечают всем критериям формирования и развития логического мышления.

Главным звеном в формировании геометрических понятий в начальных классах является преемственность в изучении материала, т. е. новые знания должны строиться с учетом тех, что были получены в дошкольном возрасте. Первоклассники без труда могут назвать геометрическую фигуру по ее наглядному образу, не принимая во внимание совокупность существенных признаков. В связи с эти нередко возникают ошибки. Например, сравнивая фигуры, учащиеся нередко проводят параллели между их цветом, размером, расположением в пространстве.

Изучение геометрического материала в начальной школе — одна из нерешенных проблем в методике на данный момент. Составители учебников не выделяют геометрических материал в самостоятельный раздел. Он включается в программу на каждом году обучения математике. Связь обычно прослеживается в установлении отношения между числом и геометрической фигурой. То же самое мы видим и в обратном направлении: число используется для изучения свойств некоторых геометрических объектов. На первом году обучения геометрические фигуры используются для присчитывания объектов как счетный материал, составления краткого условия задачи, схем, объясняющих выполнение того или иного арифметического действия и т. д. Все это приводит к тому, что в начальных классах развитие логического мышления детей не протекает должным образом что в итоге дает отрицательные результаты динамики индивидуального развития в последующем.

Во многом формированию логического мышления способствуют задания, побуждающие детей к размышлению. Их выполнение должно подкрепляться приемами, связанными с логическими формами мышления. Среди таких выделяют следующие: сравнение, анализ, синтез, обобщение, классификация и т. д.

Опираясь на тему нашего исследования, мы решили выяснить, какие задания геометрического характера, способствующие развитию логических УУД школьников, используют методисты. На данном этапе написания работы нами была выбрана программа «Школа России» (авторов М. И. Моро М. А. Бантовой и др.). С точки зрения геометрии курс предполагает формирование у детей пространственных представлений, ознакомление учащихся с основными геометрическими фигурами и некоторыми их свойствами, с простейшими чертежными и измерительными приборами. Геометрический материал предусмотрен программой для каждого класса.

Анализ данного УМК позволил нам выявить следующие приемы, связанные с логическими формами мышления.

1. Прием сравнения.

Сравнение — это «сопоставление предметов и явлений с целью нахождения сходства и различия между ними» [12, с. 74]. Сравнивая предметы друг с другом, учащиеся приходят к выводу, что с одной стороны эти предметы имеют сходства, с другой — определенные отличия. Рассмотрим подробно несколько заданий из учебников по математике УМК «Школа России».

Задание 1. Сравни, чем фигуры на рисунке слева отличаются от фигур на рисунке справа [4, с. 50].

Цель данного задания: познакомить учащихся с понятиями круг, четырехугольник, многоугольник.

Рис. 1. Задание на знакомство с понятиями [4, с. 50]

Важно добиться от учащихся того, чтобы они не ограничивались в сравнении фигур по размеру или цвету. Для этого учитель показывает модель круга и модель четырехугольника, предлагая учащимся прокатить по столу вначале первую фигуру, затем — вторую. Делается вывод, что второй фигуре мешают катиться углы, их много, следовательно, данная фигура называется «многоугольником». Учащиеся самостоятельно подводят итог: «Фигуры справа похожи тем, что у них есть 4 угла — они многоугольники. У фигур слева нет углов, они легко катятся — значит, эти фигуры не являются многоугольниками».

Задание 2. Сколько на чертеже ломаных? Сколько многоугольников? [4, с. 71].

Цель задания: закрепить в сознании учащихся знания о замкнутых и незамкнутых ломаных линиях, многоугольниках.

Рис. 2. Задание на сопоставление геометрических фигур [4, с. 71]

На практике при решении данного вида задания учитель и учащиеся могут столкнуться со следующим: ученик с уверенностью отнесет 1 и 4 фигуры к многоугольникам, 2 и 3 фигуры — к ломаным, в большинстве случаев забывая о понятии «замкнутая ломаная».

Подобная ошибка также может быть допущена при решении такого задания, как, например, сравнить прямоугольник с квадратом и ответить на следующий вопрос: «Как вы думаете, какое понятие шире: прямоугольника или квадрата?».

Рис. 3. Сравнение геометрических фигур

На данный вопрос учащиеся могут дать следующие ответы: «Понятие прямоугольника шире, потому что он шире квадрата», «Понятие квадрата шире, потому что на доске изображенный квадрат больше, чем прямоугольник», «Если мы наложим квадрат на прямоугольник, то увидим, что прямоугольник будет шире».

Помимо разобранных нами заданий, в учебниках по математике УМК «Школа России» встречаются следующие задания: «Какая фигура пропущена?», «Какие фигуры изображены на чертеже. На какие две группы их можно разбить? Найди разные способы», «Какая фигура лишняя?».

Из данных примеров мы видим, что прием сравнения, в свою очередь, подразделяется на два приема: прием сопоставления и противопоставления. Начиная с первого класса использование этих приемов позволяет учащимся сформулировать понятия(множество треугольников, множество многоугольников, множество отрезков и т. д.). В дальнейшем — представления о свойствах фигур и их классификациях.

2. Приемы анализа и синтеза.

Если анализ — «это мысленное расчленение предмета или явления на образующие его части или мысленное выделение в нем отдельных свойств, черт, качеств» [12, с. 14], то в процессе практических действий учащиеся замечают, что в отличие от приема анализа, синтез способствует объединению элементов, дает знание об объекте в целом. В каждом сложном мыслительном процессе эти два приема участвуют в единстве. Совместное их использование дает возможность получения более детальных знаний о геометрическом объекте.

Нами были выявлены следующие задания.

Задание 1. Рассмотри чертежи и объясни, почему: это ломанные, а это не ломанные [4, с. 42].

Цель задания: закрепить изученные свойства ломаной линии.

Рис. 4. Закрепление изученных свойств [4, с. 42]

Анализируя данные фигуры, учащиеся приходят к следующим выводам: ломая — это та фигуры, в которой никакие два соседних звена не лежат на одной прямой (отл. фигура № 4), у ломаной линии конец одного отрезка начало другого (отл. фигура № 3). Для того чтобы данное задание способствовало развитию логического мышления школьника, учитель должен позволить учащимся самостоятельно подвести итог. Для этого возможно организовать работу в парах/группах.

Задание 2. Почему каждую фигуру можно назвать лишней? [6, с. 4]

Цель задания: устанавливать соответствие между фигурами и их свойствами.

Рис 5. Задание на установление соответствия между фигурами [6, с. 4]

Ответы учащихся на данный вопрос будут варьироваться в зависимости от степени сформированности логического мышления и творческих возможностей учащихся. Ответы могут быть следующими: «Лишняя фигура 1, потому что это треугольник, а остальные фигуры — четырехугольники», «Лишняя фигура 2, потому что у нее все углы прямые», «Лишняя фигура 3, потому что длины ее сторон различны, а в других двух фигурах стороны равны» и т. д. Желательно не допускать ответов: «Лишняя фигура 2, потому что она отлична по цвету». Цель данного задания: закрепление свойств геометрических фигур, поэтому отличие фигур по цветовой гамме — ответ, лежащий на поверхности и не требующий от учащихся глубоких логических рассуждений.

К данным приемам, анализируя страницы учебников, мы отнесли также следующие задания: «Запишите номера всех прямоугольников/квадратов», «Рассмотри рисунок. Выбери высказывания, верные для этого рисунка», «Начерти в тетради такие фигуры. Проведи в каждой фигуре один отрезок так, чтобы стало видно, что все три фигуры имеют одинаковые площади».

3. Прием обобщения.

Чаще всего прием обобщения используется при формулировке определений, правил, свойств геометрических фигур. Нередко учащиеся допускают ошибки при использовании обобщения, так как не умеют выделять из общего существенные признаки геометрических объектов.

В УМК «Школа России» прослеживаются следующие задания.

Задание 1. Сколько треугольников на чертеже? Сколько квадратов? [4, с. 55].

Рис. 6. Задание на обобщение [4, с. 55]

Часто учащиеся затрудняются при выполнении подобного задания, сталкиваясь с отличием в изображении фигур от того образа, который сложился у них в дошкольном возрасте.

Например, учащиеся без труда ответят, что 1 фигура квадрат, но допустят ошибку, если изменить положение фигуры в пространстве (фигура 2):

Рис 7. Задание на устранение ошибок

Задание 2. Как можно одним словом назвать все фигуры на чертеже? Какую фигуру можно назвать лишней? [4, с. 78]

Цель: узнавание математического объекта по заданным признакам.

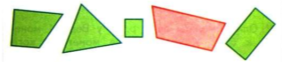
1 2 3 4 5

Рис. 8. Задание на узнавание геометрической фигуры

Ошибочным будет рассуждение учащихся: «Лишней фигура будет та, которая красная, потому что все остальные многоугольники — зеленые». Для этого учитель может предложить свое задание: «На какие еще группы можно разделить все многоугольники на чертеже». После этого учащимися будет сделан вывод, что, 1, 3, 4 и 5 фигуры — это четырехугольники, 2 фигура — треугольник. Затем учитель возвращается ко второму вопросу задания: «Какую фигуру можно назвать лишним». Исходя из вывода, сделанного учащимися ранее, они подведут следующий итог: «Лишняя фигура № 2 — это треугольник. Остальные фигуры на чертеже — четырехугольники».

На наш взгляд, содержание программы и различные методические подходы к реализации заданий способствуют развитию логического мышления младшего школьника, а целенаправленная и систематическая работа учителя на уроках математики по формированию логических УУД при использовании приемов сравнения, анализа, синтеза и обобщения, способствует развитию интеллекта и творческих способностей учащихся.

Литература:

1. Выготский Л. С. Педагогическая психология / Л. С. Выготский. — М.: Педагогика, 1991. — 536 с.
2. Гальперин П. Я. К исследованию интеллектуального развития ребенка.//Вопросы психологии, 1969, № 1. — с.15–25.
3. Леонтьев, А. Н. Деятельность. Сознание. Личность / А. Н. Леонтьев — М.: Политиздат, 1975. — 312 с.
4. Моро. М. И. Математика. 1 класс. Учеб. для общеобразоват. учрежденийсприл. на электрон. носителе. В 2 ч. Ч. 1 / М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. — 3-е изд. — М.: Просвещение, 2014. — 127 с.: ил. — (Школа России).
5. Моро. М. И. Математика. 1 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. — 3-е изд. — М.: Просвещение, 2014. — 112 с.: ил. — (Школа России).
6. Моро. М. И. Математика. 2 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. — 3-е изд. — М.: Просвещение, 2014. — 95 с.: ил. — (Школа России).
7. Моро. М. И. Математика. 2 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. — 3-е изд. — М.: Просвещение, 2014. — 112 с.: ил. — (Школа России).
8. Моро. М. И. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. — 3-е изд. — М.: Просвещение, 2014. — 112 с.: ил. — (Школа России).
9. Моро. М. И. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. — 3-е изд. — М.: Просвещение, 2014. — 112 с.: ил. — (Школа России).
10. Моро. М. И. Математика. 4 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. — 3-е изд. — М.: Просвещение, 2014. — 112 с.: ил. — (Школа России).
11. Моро. М. И. Математика. 4 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. — 3-е изд. — М.: Просвещение, 2014. — 127 с.: ил. — (Школа России).
12. Педагогический словарь: Для студ. высш. и сред. пед. учеб. заведений / сост. Г. М. Коджаспирова, А. Ю. Коджаспиров. — М.: Издательский центр «Академия», 2003. — 176 с.
13. Пиаже, Ж. Избранные психологические труды: Психология интеллекта. Генезис числа у ребенка. Логика и психология. / Ж. Пиаже; пер. с франц. — М.: Педагогика, 2001. — 589 с.
14. Рубинштейн, С. Л. Основы общей психологии. / С. Л. Рубинштейн. — СПб.: Питер, 2007. — 310 с.
15. Талызина Н. Ф. Теория поэтапного формирования умственных действий и проблемы развития мышления в процессе обучения в школе// Советская педагогика.- 1967, № 1. — с.28–32
16. Талызина Н. Ф. Управление процессом усвоения знаний / Н. Ф. Талызина. –М.: МГУ,1975.- 343 с.