Метод наименьших квадратов в оценке параметров надежности при нормальном законе распределения отказов | Статья в журнале «Молодой ученый»

Отправьте статью сегодня! Журнал выйдет 28 декабря, печатный экземпляр отправим 1 января.

Опубликовать статью в журнале
Проекты
Меню
Поиск
+7 (843) 500-57-53
info@moluch.ru
Личный кабинет

Метод наименьших квадратов в оценке параметров надежности при нормальном законе распределения отказов

Авторы: ,

Рубрика: Информационные технологии

Опубликовано в Молодой учёный №25 (315) июнь 2020 г.

Дата публикации: 20.06.2020

Статья просмотрена: 214 раз

Скачать электронную версию

Скачать Часть 2 (pdf)

Библиографическое описание:

Ковальчук, В. В. Метод наименьших квадратов в оценке параметров надежности при нормальном законе распределения отказов / В. В. Ковальчук, М. С. Бурзун. — Текст : непосредственный // Молодой ученый. — 2020. — № 25 (315). — С. 99-104. — URL: https://moluch.ru/archive/315/71945/ (дата обращения: 18.12.2024).



В статье показан пример расчета показателей надежности работы системы методом наименьших квадратов средствами VBA.

Ключевые слова: безотказная работа, доверительный интервал, испытания, метод наименьших квадратов, нормальный закон распределения, число отказов.

При нормальном законе распределения отказов сначала необходимо определить оценки математического ожидания и среднеквадратичного отклонения, а затем рассчитать вероятность отказа, частоту и интенсивность отказов [1].

Для определения математического ожидания и среднеквадратичного отклонения для каждого разряда статистического ряда подсчитывают q i с использованием выражения и по таблице квантилей нормального закона распределения определяют значения квантилей [2, 3].

Листинг фрагмента программы расчета показателей при нормальном законе распределения:

'Вычислим 11 строку таблицы(13)=============================qi

СтрокаТаблицы = 13

СтолбецТаблицы = 4

СуммаВышедшихЗаПериод = 0

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы - 1)

СуммаВышедшихЗаПериод = СуммаВышедшихЗаПериод + Sheets("ОсновнаяТаблица").Cells(4, n).Value

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, n).Value = СуммаВышедшихЗаПериод / КоличествоЭлементов

Next

'Вычислим 12 строку таблицы(14)=============================p

СтрокаТаблицы = 14

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы - 1)

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, n).Value = 1 - Sheets("ОсновнаяТаблица").Cells(13, n).Value

Next

'Вычислим 13 строку таблицы(15)=============================Uqi

СтрокаТаблицы = 15

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы - 1)

p = Sheets("ОсновнаяТаблица").Cells(14, n).Value

СтрокаТаблицыПриложения = 2

' проверим попадают ли входные данные в значения таблицы

While Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения, 1).Value <> ""

СтрокаТаблицыПриложения = СтрокаТаблицыПриложения + 1

Wend

If p <= Sheets("Квантили норм распределения").Cells(2, 1).Value Then

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, n).Value = Round(Sheets("Квантили норм распределения").Cells(2, 2).Value * (-1), 3)

GoTo СледующийПоиск

End If

If p >= Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения - 1, 1).Value Then

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, n).Value = Round(Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения - 1, 2).Value * (-1), 3)

GoTo СледующийПоиск

End If

СтрокаТаблицыПриложения = 2

While Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения, 1).Value <> ""

If Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения, 1).Value = p Then

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, n).Value = Round(Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения, 2).Value * (-1), 3)

GoTo СледующийПоиск

End If

If p < Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения, 1).Value And p > Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения - 1, 1).Value Then

If Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения, 1).Value - p < p - Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения - 1, 1).Value Then

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, n).Value = Round(Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения, 2).Value * (-1), 3)

Else

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, n).Value = Round(Sheets("Квантили норм распределения").Cells(СтрокаТаблицыПриложения - 1, 2).Value * (-1), 3)

End If

GoTo СледующийПоиск

End If

СтрокаТаблицыПриложения = СтрокаТаблицыПриложения + 1

Wend

СледующийПоиск:

Next

Результаты расчета представлены в таблице Excel (Таблица 1).

Таблица 1

Результаты расчета основных показателей испытаний

Разряды

1

2

3

4

5

6

7

8

9

10

qi

0,05

0,08

0,13

0,15

0,17

0,2

0,23

0,26

0,31

0,34

Uqi

-1,645

-1,405

-1,126

-1,036

-0,954

-0,842

-0,739

-0,643

-0,496

-0,412

В случае усеченной выборки, при проведении испытаний, когда в результате испытаний получены r значений наработки ( r < N ) для отказавших изделий t 1 , …, t r , а N — r изделий остались исправными после испытаний, параметры T ср и σ можно оценить по методу квантилей.

(1)

(2)

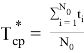
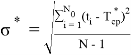
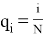
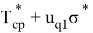
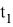
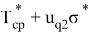
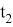
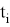
Считая, что за время t i вероятность выхода из строя испытуемых изделий составляет , где i – число отказавших изделий за время t i . Для этой вероятности находят квантили Uq i , по таблице квантилей нормального распределения и составляют систему уравнений:

=

=

……………….

= (3)

Полученную систему уравнений решают по методу наименьших квадратов. Все уравнения складывают, в результате чего получают первое нормальное уравнение.

(4)

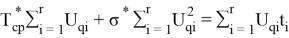
Второе нормальное уравнение получают суммированием исходной системы уравнений (3)

(5)

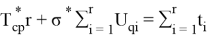
Уравнения (4) и (5) решают относительно неизвестных T* ср и σ* и находят их оценки.

'Составляем системы уравнений

СтолбецТаблицы = 4

СтрокаПВ = 1

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы - 1)

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 1).Value = Sheets("ОсновнаяТаблица").Cells(3, n).Value

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 2).Value = "="

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 3).Value = 1

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 4).Value = "Тср"

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 5).Value = Sheets("ОсновнаяТаблица").Cells(15, n).Value

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 6).Value = Sheets("Оформление").Cells(1, 5).Value

СтрокаПВ = СтрокаПВ + 1

Next

'Суммируем систему уравнений

СтрокаПВ = 1

СуммаВремИнтервалов = 0

СуммаТср = 0

СуммаСигм = 0

While Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 1).Value <> ""

СуммаВремИнтервалов = СуммаВремИнтервалов + Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 1).Value

СуммаТср = СуммаТср + Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 3).Value

СуммаСигм = СуммаСигм + Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 5).Value

СтрокаПВ = СтрокаПВ + 1

Wend

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 1).Value = СуммаВремИнтервалов

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 1).Font.Bold = True

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 2).Value = "="

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 2).Font.Bold = True

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 3).Value = СуммаТср

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 3).Font.Bold = True

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 4).Value = "Тср"

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 4).Font.Bold = True

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 5).Value = СуммаСигм

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 5).Font.Bold = True

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 6).Value = Sheets("Оформление").Cells(1, 5).Value

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 6).Font.Bold = True

'Умножаем на соответствующий квантиль uqi левые и правые части уравнений, получим новую систему уравнений.

СтолбецТаблицы = 4

СтрокаПВ = 1

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы - 1)

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 10).Value = Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 1).Value * Sheets("ОсновнаяТаблица").Cells(15, n).Value

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 11).Value = Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 2).Value

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 12).Value = Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 3).Value * Sheets("ОсновнаяТаблица").Cells(15, n).Value

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 13).Value = Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 4).Value

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 14).Value = Round(Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 5).Value * Sheets("ОсновнаяТаблица").Cells(15, n).Value, 3)

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 15).Value = Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 6).Value

СтрокаПВ = СтрокаПВ + 1

Next

'Складываем все полученные уравнения, в результате получаем первое нормальное уравнение

СтрокаПВ = 1

СуммаВремИнтервалов = 0

СуммаТср = 0

СуммаСигм = 0

While Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 10).Value <> ""

СуммаВремИнтервалов = СуммаВремИнтервалов + Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 10).Value

СуммаТср = СуммаТср + Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 12).Value

СуммаСигм = СуммаСигм + Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 14).Value

СтрокаПВ = СтрокаПВ + 1

Wend

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 10).Value = СуммаВремИнтервалов

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 10).Font.Bold = True

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 11).Value = "="

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 11).Font.Bold = True

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 12).Value = СуммаТср

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 12).Font.Bold = True

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 13).Value = "Тср"

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 13).Font.Bold = True

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 14).Value = СуммаСигм

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 14).Font.Bold = True

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 15).Value = Sheets("Оформление").Cells(1, 5).Value

Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 15).Font.Bold = True

'Решаем систему уравнений вида

'a=b*X+c*Y

'n=m*X+k*Y

'находим строку в таблице где у нас находятся уравнения

СтрокаПВ = 1

While Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 1).Value <> ""

'СуммаВремИнтервалов = СуммаВремИнтервалов + Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 10).Value

'СуммаТср = СуммаТср + Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 12).Value

'СуммаСигм = СуммаСигм + Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 14).Value

СтрокаПВ = СтрокаПВ + 1

Wend

СтрокаПВ = СтрокаПВ - 1

a = Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 1).Value

b = Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 3).Value

c = Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 5).Value

n = Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 10).Value

m = Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 12).Value

k = Sheets("Промежуточные вычисления").Cells(СтрокаПВ, 14).Value

Сигма = (b * n - m * a) / (b * k - m * c)

Tcp = (a - c * Сигма) / b

Sheets("Промежуточные вычисления").Cells(СтрокаПВ + 2, 1).Value = "Tcp"

Sheets("Промежуточные вычисления").Cells(СтрокаПВ + 2, 2).Value = "="

Sheets("Промежуточные вычисления").Cells(СтрокаПВ + 2, 3).Value = Tcp

Sheets("Промежуточные вычисления").Cells(СтрокаПВ + 3, 1).Value = Sheets("Оформление").Cells(1, 5).Value

Sheets("Промежуточные вычисления").Cells(СтрокаПВ + 3, 2).Value = "="

Sheets("Промежуточные вычисления").Cells(СтрокаПВ + 3, 3).Value = Сигма

'

Суммируя систему уравнений, определяют второе нормальное уравнение:

550= Т ср — 9,298 σ, (6)

Умножая на соответствующий квантиль u qi левые и правые части уравнений, получают новую систему уравнений.

Складывая все полученные уравнения, в результате получают первое нормальное уравнение:

—407= -9,298Т ср + 10,015 σ,(7)

Решив совместно уравнения (6.1) и (6.2), получают

Т ср = 125,86 ч.

σ = 76,21 ч.

'Заполним 14 строку таблицы(16)=============================Тср

СтрокаТаблицы = 16

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы - 1)

Next

СтолбецТаблицы = 4

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, СтолбецТаблицы).Value = Round(Tcp, 2)

Sheets("ОсновнаяТаблица").Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n - 1)).MergeCells = True

Sheets("ОсновнаяТаблица").Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n - 1)).HorizontalAlignment = xlCenter

'Заполним 15 строку таблицы(17)=============================Сигма

СтрокаТаблицы = 17

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы - 1)

Next

СтолбецТаблицы = 4

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, СтолбецТаблицы).Value = Round(Сигма, 2)

Sheets("ОсновнаяТаблица").Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n - 1)).MergeCells = True

Sheets("ОсновнаяТаблица").Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n - 1)).HorizontalAlignment = xlCenter

Для «стареющих» элементов в качестве распределения интервала безотказной работы используют нормальное распределение. Испытания могут проводиться до возникновения определенного числа отказов или прекращения испытаний после истечения заданного количества часов.

Литература:

  1. Коваленко, В. Н., Новиков, А. А. Надежность устройств железнодорожной автоматики, телемеханики и связи. учеб. пособие. — Екатеринбург: УрГУПС, 1995. — с. 78.
  2. Основы теории надежности автоматических систем управления: учеб. пособие для вузов / Л. П. Глазунов, В. П. Грабовецкий, О. В. Щербаков. — Л.: Энергоатомиздат, Ленинградское отд-ние, 1984. — 208 с.
  3. Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся ВТУЗов. — М.: Наука, 1980. — 976 с.
Основные термины (генерируются автоматически): вычисление, система уравнений, нормальное уравнение, строка таблицы, VBA, безотказная работа, математическое ожидание, нормальное распределение, правая часть уравнений, среднеквадратичное отклонение.


Ключевые слова

испытания, метод наименьших квадратов, безотказная работа, доверительный интервал, нормальный закон распределения, число отказов

Похожие статьи

Оценка показателей надежности испытаний при экспоненциальном законе распределения отказов

В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами VBA.

Оценка параметров надежности при нормальном законе распределения отказов средствами Excel

В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами Excel.

Метод оценки нормальности распределения результатов измерений по критерию согласия Пирсона на основе Excel

В статье описывается алгоритм обработки статистических данных на основе процедуры проверки нормальности распределения значений результатов измерения по критерию Пирсона с помощью программы Excel. Рассматриваются преимущества автоматического счета пок...

Проверка численных моделей открытых СМО с ограничениями

Рассматривается численная модель открытой системы массового обслуживания, степень влияния соотношения входных параметров системы на погрешность вычисляемых динамических значений характеристик.

Использование обобщенных параметров группирующихся стираний и ошибок для адаптивного выбора длины блока в системах передачи данных

В статье рассмотрена иерархическая модель источника ошибок и стираний, описываемая моделью Пуртова с Марковской цепью переходов состояний при передаче данных по нестационарным каналам. Установлена зависимость степени группирования, средней кратности ...

Задача теории расписаний с временем поступления и временем доставки

В данной работе рассматривается применение аппроксимационных алгоритмов с гарантированной оценкой точности к задаче составления расписания на одном процессоре, где каждая работа имеет время выпуска, время обработки и время доставки.

О непараметрическом восстановлении матрицы наблюдений с пропусками в задаче идентификации с шумами

Исследуется задача восстановления матрицы наблюдений «входных-выходных» переменных в задаче идентификации статических систем с помехами. Часто эта задача сводится к восстановлению регрессионных характеристик. Анализируется случай, когда измерения «вх...

Исследование процессов обработки и преобразования параметров тестовых заданий в интеллектуальной обучающей системе

В статье рассматриваются вопросы калибровки банка тестовых заданий в интеллектуальной обучающей системе. Выделяются уровни сложности заданий, что позволяет наложить на них дополнительные ограничения, и приводится диапазон сложности заданий для каждог...

Сравнительный анализ численного решения задач оптимального управления

Данная работа посвящена анализу численных методов решения задач оптимального управления: метода последовательных приближений и метода вариации. Работа данных алгоритмов была апробирована на конкретном тестовом примере с известным аналитическим решени...

Методика анализа и схема алгоритма анализа динамических погрешностей отработки программной траектории

В данной статье рассмотрены методики анализа динамических погрешностей отработки программной траектории. На основе проведенного исследования автором предлагается блок-схема обобщенного алгоритма вычисления погрешности.

Похожие статьи

Оценка показателей надежности испытаний при экспоненциальном законе распределения отказов

В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами VBA.

Оценка параметров надежности при нормальном законе распределения отказов средствами Excel

В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами Excel.

Метод оценки нормальности распределения результатов измерений по критерию согласия Пирсона на основе Excel

В статье описывается алгоритм обработки статистических данных на основе процедуры проверки нормальности распределения значений результатов измерения по критерию Пирсона с помощью программы Excel. Рассматриваются преимущества автоматического счета пок...

Проверка численных моделей открытых СМО с ограничениями

Рассматривается численная модель открытой системы массового обслуживания, степень влияния соотношения входных параметров системы на погрешность вычисляемых динамических значений характеристик.

Использование обобщенных параметров группирующихся стираний и ошибок для адаптивного выбора длины блока в системах передачи данных

В статье рассмотрена иерархическая модель источника ошибок и стираний, описываемая моделью Пуртова с Марковской цепью переходов состояний при передаче данных по нестационарным каналам. Установлена зависимость степени группирования, средней кратности ...

Задача теории расписаний с временем поступления и временем доставки

В данной работе рассматривается применение аппроксимационных алгоритмов с гарантированной оценкой точности к задаче составления расписания на одном процессоре, где каждая работа имеет время выпуска, время обработки и время доставки.

О непараметрическом восстановлении матрицы наблюдений с пропусками в задаче идентификации с шумами

Исследуется задача восстановления матрицы наблюдений «входных-выходных» переменных в задаче идентификации статических систем с помехами. Часто эта задача сводится к восстановлению регрессионных характеристик. Анализируется случай, когда измерения «вх...

Исследование процессов обработки и преобразования параметров тестовых заданий в интеллектуальной обучающей системе

В статье рассматриваются вопросы калибровки банка тестовых заданий в интеллектуальной обучающей системе. Выделяются уровни сложности заданий, что позволяет наложить на них дополнительные ограничения, и приводится диапазон сложности заданий для каждог...

Сравнительный анализ численного решения задач оптимального управления

Данная работа посвящена анализу численных методов решения задач оптимального управления: метода последовательных приближений и метода вариации. Работа данных алгоритмов была апробирована на конкретном тестовом примере с известным аналитическим решени...

Методика анализа и схема алгоритма анализа динамических погрешностей отработки программной траектории

В данной статье рассмотрены методики анализа динамических погрешностей отработки программной траектории. На основе проведенного исследования автором предлагается блок-схема обобщенного алгоритма вычисления погрешности.

Задать вопрос