Определение коэффициента гидравлического сопротивления и безразмерной функции Леверетта в пластовых условиях



В статье выведены формулы для определения коэффициента гидравлического сопротивления при двухфазной фильтрации, а так же для безразмерной функции Леверетта в пластовых условиях.

Ключевые слова: коэффициент, гидравлическое сопротивление, двухфазная фильтрация, функция Леверетта.

The article presents formulas for determining the coefficient of hydraulic resistance for two-phase filtration, as well as for the dimensionless Leverett function in reservoir conditions.

Keywords: coefficient, hydraulic resistance, two-phase filtration, Leverett function.

При движении жидкостей и газов в пористой среде в силу причудливой формы поровых каналов граница раздела фаз имеет сложную поверхность с большой площадью. Это является причиной того, что на движение и равновесие жидкостей, в пористой среде определяющее влияние оказывают поверхностные явления и капиллярные силы.

Существование поверхностного натяжения приводит к деформации поверхности раздела так, что ее поверхность оказывается минимальной. По этой причине капли жидкости, и пузырьки газа принимают сферическую форму. На искривленной поверхности раздела двух фаз давление претерпевает скачок. Так, например, давление внутри, капли выше, чем снаружи. Разность давлений по обеим частям искривленной поверхности раздела называется поверхностным или капиллярным давлением и вычисляется по формуле Лапласа:

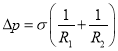
где и

— главные радиусы кривизны межфазной поверхности, — коэффициент поверхностного натяжения.

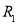
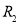
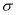
Для определения эффективного перепада давления двигающейся (при пропитки пористой среды смачивающей фазой) используется формула:

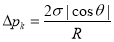
где радиус капилляра, - угол смачивания. Здесь , - давление в не смачивающейся, — давление в смачивающейся жидкости.

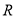
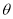
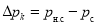
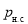
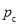
Учитывая, что то для пластовых условий можно написать

или (1)

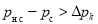
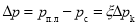
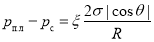
Здесь , - давления (соответственно) на контуре и на призабойной зоне, - поправочный коэффициент, - эффективный радиус.

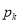
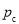
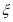
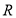
где

.

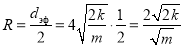
При двухфазной фильтрации эффективный диаметр запишем в виде:

(2)

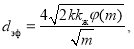
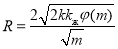
Здесь — абсолютная, - относительная фазовая проницаемости, - функция, зависимая от пористости.

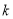
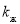
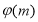
Тогда для определения безразмерной функции Леверетта используем формулы (1) и (2):

или (3)

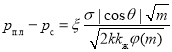
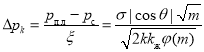
Окончательно для безразмерной функции Леверетта можно написать

(4)

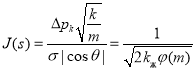
Следует отметить, что для эффективного диаметра существуют различные формулы. Поэтому для функции Леверетта в наиболее общем виде можно написать формулу в виде:

. Здесь - можно определять по данным лабораторных и гидрогазодинамических исследований.

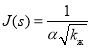
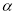
А теперь напишем формулы для определения коэффициента гидравлического сопротивления. Как известно [1,2,3]:

, , (5)

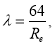
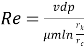
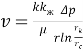
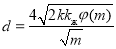
где - плотность флюида, - депрессия, , — радиусы, контура и призабойной зоны.

(6)

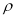
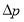
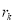
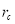
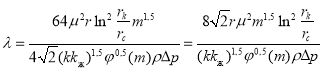
При однофазной фильтрации . Если взять, то получим известную формулу для коэффициента гидравлического сопротивления [2,3,4].

(7)

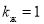
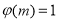
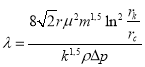
Таким образом, в данной статье для безразмерной функции Леверетта предложена простая формула в зависимости от относительной проницаемости нефти в пластовых условиях.

Литература:

1. Басниев К. С. Нефтегазовая гидромеханика /К. С. Басниев, Н. М. Дмитриев, Г. Д. Розенберг. — Москва-Ижевск: Институт компьютерных исследований, 2005.
2. Гасанов И. Р. Квопросу определения гидравлического сопротивления при двучленном законе фильтрации углеводородов в пористой среде с учетом влияния начального градиента. «Молодой учёный. Международный научный журнал» № 49 (235) / 2018 с.27–29
3. Гасанов И. Р. Об определении гидравлического сопротивления при турбулентном режиме фильтрации флюида в пористой среде. «Молодой учёный. Международный научный журнал» № 2 (240) / 2019 с.20–22
4. И. Р. Гасанов, М. А. Джамалбеков. К вопросу определения коэффициента гидравлического сопротивления при фильтрации флюидов в нефтегазовых и газоконденсатных месторождениях. Международный научный журнал «Молодой учёный» № 15(305) — 2020 Апрель, с. 98–101.