В статье рассматриваются методы и общая математическая модель параметрической идентификации объектов, а также описывается теоретическая возможность использования искусственных нейронных сетей в рамках решения данной задачи.
Ключевые слова: параметрическая идентификация, объект, система, модель, искусственные нейронные сети.
Идентификация некоторого объекта представляет собой процесс нахождения оптимальной математической модели объекта, описывающей его свойства. Задача построения математической модели, как правило, заключается в определении общей структуры объекта, нахождении значений параметров и, если нужно, значений зависимых переменных, например, переменных состояния [1, с. 35].
Методы идентификации
Методы идентификации не всегда позволяют построить сложную математическую модель, эквивалентную по структуре и параметрам реальному объекту. Однако это не мешает использовать такую модель, если она отражает основные свойства объекта.
Идентификацию можно провести как методами экспериментального, так и методами физико-математического анализа. Первые предполагают построение математической модели исследуемого объекта по измерениям его входных и выходных величин. При идентификации методами физико-математического анализа исходят из математического описания и конструктивных аспектов простейших процессов, которые относятся к изучаемому объекту. В итоге получают систему алгебраических и дифференциальных уравнений, содержащих не только входные и выходные переменные, но и переменные состояния. В эти уравнения иногда включаются избыточные внутренние переменные объекта [1, с. 36].
Порядок идентификации
Порядок идентификации объектов некоторой вычислительной системы описанными методами представлен на рис. 1.
![Схема идентификации объектов вычислительной системы [2, с. 130]](https://moluch.ru/blmcbn/72192/72192.001.png)
Рис. 1. Схема идентификации объектов вычислительной системы [2, с. 130]
На первом этапе разрабатывают так называемую функциональную модель. При этом, как правило, выбирают математический аппарат, с помощью которого можно адекватно описать объект. Затем к исследуемому объекту подключают средства измерений. Получаемые ими данные используются системой оценки параметров и характеристик для вычисления параметров
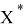
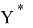
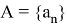
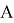
Значения параметров
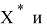
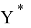
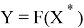
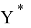
Применение искусственных нейронных сетей для идентификации
Искусственные нейронные сети применяются для решения задач искусственного интеллекта: например, для распознавания или классификации некоторых объектов. Поэтому для них задача идентификации формулируется применительно к таким объектам, а не к сети. Ее решение сводится к следующим основным операциям:
1) выбор набора признаков, характеризующих объект;
2) выбор структуры сети;
3) выбор критерия эффективности сети;
4) выбор метода настройки сети.
Первая операция зачастую зависит от назначения системы и свойств объектов, подлежащих идентификации.
Что касается структуры: считается, что наиболее перспективными являются сверточные и рекуррентные сети [3, с. 41]. Сверточные сети обладают высокой эффективностью в решении задач распознавания двумерных и трехмерных объектов. Обучение такой сети с нуля на небольшом объеме обучающих данных дает достаточно высокие результаты, несмотря на относительную нехватку данных [4, с. 160].
В параметрической идентификации используют, в основном, рекуррентные сети. В работе [5] демонстрируется, что с помощью рекуррентной сети с обратной связью и внутренним слоем можно провести достаточно точную параметрическую идентификацию технологического объекта — теплообменника, аппроксимируя частотные характеристики модели передаточными функции. В работе [6] на примере двухмассовой электромеханической системы была доказана эффективность использования рекуррентной сети Элмана с применением квазиньютоновских методов оптимизации в рамках решения задачи параметрической идентификации по переходным характеристикам объекта в процессе настройки системы.
Традиционным критерием эффективности искусственных нейронных сетей является величина отклонения выходных сигналов, формируемых сетью, от эталонных. Одним из самых распространенных методов является корень среднеквадратического отклонения — показатель рассеивания значений случайной величины относительно ее математического ожидания (выдержка из бакалаврской работы на тему «Применение радиально-базисных нейронных сетей в задачах управления технологическими процессами» (ТГУ, кафедра ПМИ, автор: В. И. Шмыров).
Определение методов настройки искусственной нейронной сети, по большей части, сводится к выбору подхода к обучению сети. Под обучением понимают выбор алгоритма обучения, подбор архитектуры сети и значений весовых коэффициентов связей, чтобы выполнение поставленной перед сетью задачи было эффективным.
Заключение
Таким образом, искусственные нейронные сети могут эффективно применяться в задачах параметрической идентификации объектов, в том числе технологических объектов. При решении таких задач используют, как правило, рекуррентные сети за счет их высокой аппроксимирующей способности. В настоящее время существует достаточно большое число программных средств для реализации искусственных нейронных сетей, что упрощает задачу исследователя.
Литература:
1. Еременко Ю. И., Полещенко Д. А. Нейроуправление. Методические указания к выполнению лабораторных работ. — Старый Оскол: СТИ МИСиС. — 2006. — 64 с.
2. Ларионов А. М., Майоров С. А., Новиков Г. И. Вычислительные комплексы, системы и сети. — Л.: Энергоатомиздат. — 1987. — 178 с.
3. Созыкин А. В. Обзор методов обучения глубоких нейронных сетей. — Вестник ЮУрГУ. Вычислительная математика и информатика. — 2017. — Т. 6, № 3. — С. 28–59.
4. Шолле Ф. Глубокое обучение на Python. — СПб.: Питер. — 2018. — 400 с.
5. Шумихин А. Г., Александрова А. С., Мустафин А. И. Параметрическая идентификация технологического объекта в режиме его эксплуатации с применением технологии нейронных сетей. — Вестник ПНИПУ. Электротехника, информационные технологии, системы управления. — 2018. — № 26. — С. 29–41.
6. Анисимов А. А., Горячев М. Н. Идентификация электромеханических систем с использованием искусственной нейронной сети. — Вестник ИГЭУ. — 2008. — № 3. — C. 55–58.







