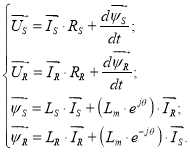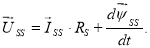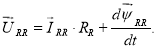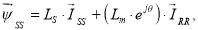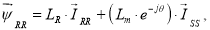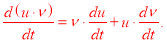При подготовке слайдов для проведения вебинаров возникла необходимость введения дополнительных обозначений при выводе уравнений асинхронного двигателя и сделаны существенные изменения в работе [1].
Основные уравнения асинхронного двигателя в векторной форме:
|
|
(1) |
|
(2) |
|
|
(3) |
|
|
(4) |
Сделаем существенное замечание по полученным векторным уравнениям. В уравнении (1) векторы
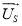
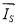
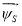
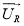
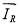
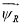
Рассмотрим схему преобразования одного из векторов, например,
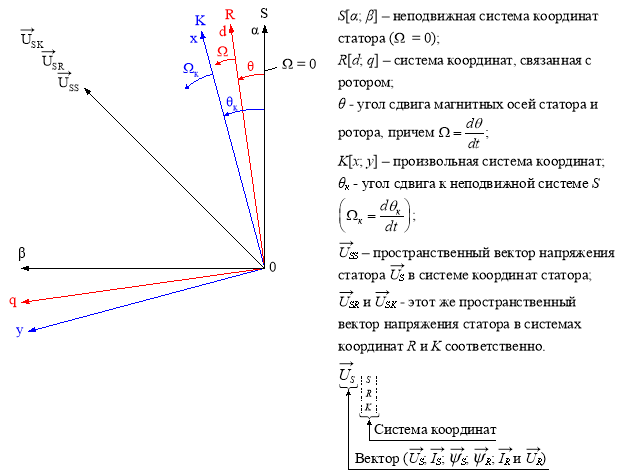
Рис. 1. Система координат S , R , K
Уравнение (1), записанное в статорной системе координат, примет следующий вид:
|
|
(1’) |
Уравнение (2) с векторными переменными в роторной системе координат:
|
|
(2’) |
В уравнении (3):
|
|
(3’) |
где
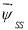
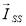
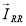
|
|
(4’) |
где
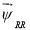
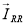
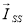
Несложно догадаться, что математическую модель асинхронного двигателя можно получить только при переводе всех уравнений (1’), …, (4’) к одной из систем координат.
Формулы приведения для напряжения

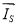
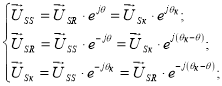
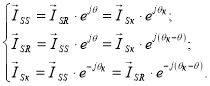
Формулы приведения для потокосцеплений
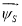
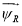
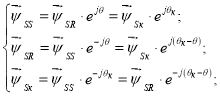
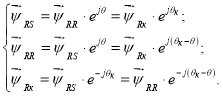
Для напряжения
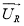
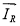
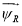
1. Приведение векторных уравнений к неподвижной системе координат.
Уравнение (1’) уже записано в статорной системе координат (
S
), поэтому показываем процесс приведения следующего уравнения. Для этого умножим обе части уравнения (2’) на
e
jθ
и сразу выразим
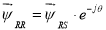

|
Правила преобразования: 1. Производная от сложной функции ( u · ν ):
2.
где α = -jθ . |
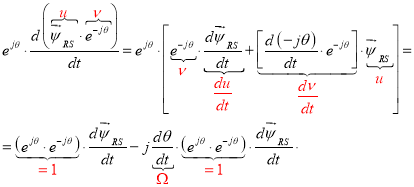
Окончательно, уравнение (2’), приведенное к статорной системе:
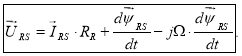
Приведение уравнения (3’) к статорной системе координат:
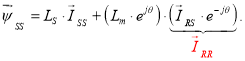
Так как произведение e jθ · e - jθ = 1, то
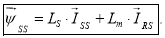
Для приведения уравнения (4’) к статорной системе координат умножим обе части на e jθ :
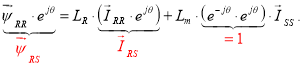
Окончательно:
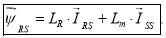
Опуская индекс «статорная система координат», получим:
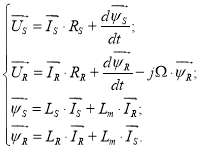
2. Приведение векторных уравнений к роторной системе координат.
Умножим обе части уравнения (1’) на
e
–
jθ
и выразим
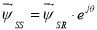

|
Правила преобразования: 1. Производная от сложной функции ( u · ν ):
2.
где α = jθ . |
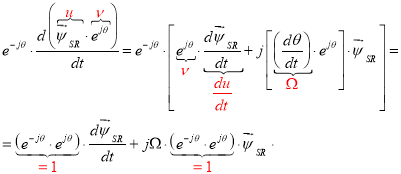
Окончательно:
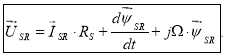
Уравнение (2’) остается без изменений, т.к. оно уже записано в роторной системе координат.
Умножим обе части уравнения (3’) на e – jθ :

Окончательно:
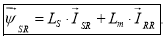
В уравнении (4’) выразим
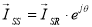
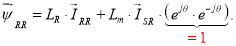
Опуская индекс «роторная система координат», получим:
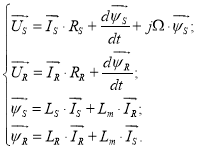
3. Приведение векторных уравнений к системе координат, вращающейся с произвольной скоростью Ω к .
Умножим обе части уравнения (1’) на
e
–
jθ
к
и сразу выразим


|
Правила преобразования: 1. Производная от сложной функции ( u · ν ):
2.
где α = jθ к . |
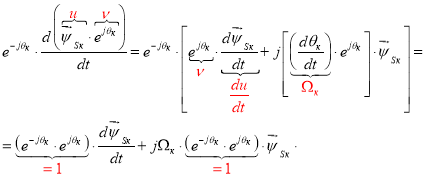
Окончательно:
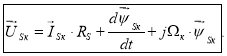
Умножим обе части уравнения (2’) на
e
–
j
(
θ
к
–
θ
)
и сразу выразим
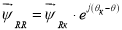
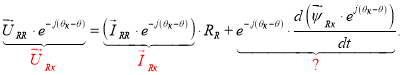
|
Правила преобразования: 1. Производная от сложной функции ( u · ν ):
2.
где α = j ( θ к – θ ). |

Окончательно:
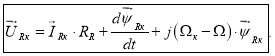
Умножим уравнение (3’) на e – jθ к , тогда
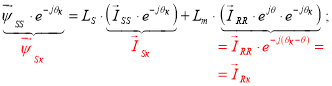

Уравнение (4’) умножим на e – j ( θ к – θ ) , тогда
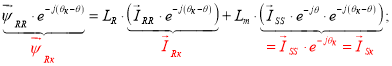
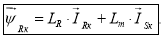
Опуская индекс «произвольная система координат», получим:
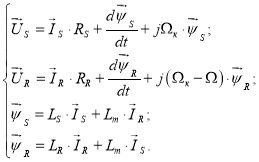
Литература:
- Пространственные векторы в асинхронном двигателе в относительной системе единиц / А. А. Емельянов, А. М. Козлов, В. В. Бесклеткин [и др.]. - Текст: непосредственный // Молодой ученый. - 2015. - № 11 (91). - С. 133-156.
- Ковач, К. П. Переходные процессы в машинах переменного тока / К. П. Ковач, И. Рац; пер. с нем. - Москва: Госэнергоиздат, 1963. - 735 c.
- Шрейнер, Р. Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р. Т. Шрейнер, А. В. Костылев, В. К. Кривовяз, С. И. Шилин. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 c. - Текст: непосредственный.
- Шрейнер, Р. Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты / Р. Т. Шрейнер. - Екатеринбург: УРО РАН, 2000. - 654 c. - Текст: непосредственный.