В работе описана реализация алгоритма выделения структурных особенностей матриц на языке C#. Представлена архитектура программы. Были проведены вычислительные эксперименты, результаты которых продемонстрированы в виде графиков.
Ключевые слова: разработка приложения, реализация алгоритма, структурные особенности, C#, архитектура приложения, анализ работы программы.
Структурный метод интегрирования систем m уравнений общего вида [1], [2].
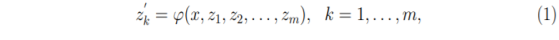
предполагает, что существует преобразование, приводящее систему (1) к виду (2)-(4)
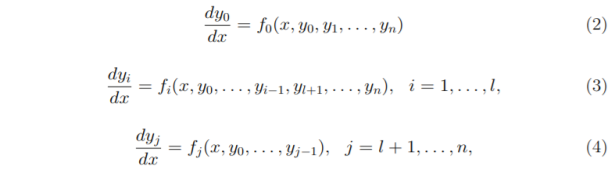
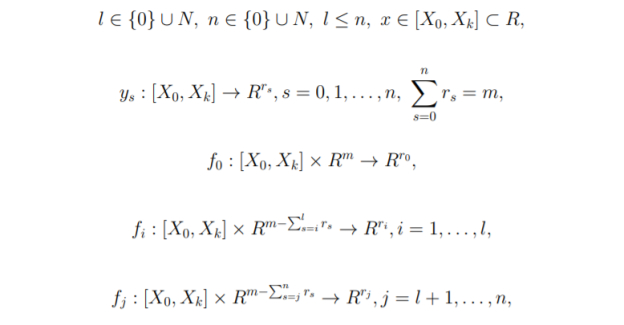
Группы (3), (4) структурно тождественны. Каждое уравнение одной из этих групп занимает определенное место в последовательности уравнений всей группы. Его правая часть не зависит от искомых функций, поведение которых описывается этим и всеми последующими уравнениями этой же группы. Группа уравнений (1) называется <<общей>> и включает в себя все уравнения, не имеющие структурных особенностей, описанных выше.
Алгоритм выделения структурных особенностей предполагает, что существует преобразование, приводящее случайную структурную матрицу к виду блочной нуль-диагональной матрицы. Задача состоит в том, чтобы найти такую перестановку π=(π(1), π(2), …, π(m)), при которой эффект от структурного подхода будет максимизирован.
В данной работе будет рассматриваться программная реализация алгоритма, выделяющего данные структурные особенности, а также анализ влияния параметров исходной структурной матрицы на быстродействие исполняемого кода.
Архитектура
Следующим шагом является разработка архитектуры программы. В работе активно используются списки (List), так как изначально неизвестен размер множеств и списки позволяют эффективно перемещаться по уровням дерева перебора. В качестве стандартов наименования была принята статья [3].
Логика работы алгоритма описана в исполняемом классе Program. Поля, начиная с omega, представлены в виде массива из двух элементов, каждый элемент массива отвечает за свое дерево перебора. Для удобства, каждый пункт алгоритма вынесен в отдельную функцию, названия которых совпадают с наименованием шага алгоритма. Основные поля и методы приведены в Листинге 0.
Листинг 0 . Класс Program
|
public class Program { public static int n; //размерность матрицы
public static List
public static int [] transition; //перестановка public static int taskType; //тип задачи private static Matrix A; //исходная структурная матрица private static int [,] B; //преобразованная структурная матрица
private static List
private static OrderedMultitude recordMultitude;//рекордное можество private static OrderedMultitude orderedMultitude;//упорядоченное множество
private static List
private static List
private static int [] searchTreeLevel; //уровни дерева перебора private static CentralElement centralElement;//центральный элемент private static PossibleExtension knotElement;//узловой элемент
private static List
public static void Main(string [] args){…} static void FirstStep(){…} private static void SecondStep(){…} private static void SecondStepA(){…} private static void SecondStepA1(){…} private static void SecondStepA1b(){…} private static void SecondStepA1c(){…} private static void SecondStepB(){…} private static void ThirdStep(){…}//перебор для задачи 1 начинается с этого пункта private static void FourthStep(){…} private static void FourthStepA(){…} private static void FourthStepA0(){…} private static void FourthStepA1a(){…} private static void FourthStepA1b(){…} private static void FourthStepA1c(){…} private static void FourthStepB(){…} private static void FourthStepB1(){…} private static void FourthStepB1a(){…} private static void FourthStepB2(){…} private static void FifthStep(){…} private static void SixthStep(){…} private static void OrderFirstMultitude(){…} private static void OrderSecondMultitude(){…} } |
Сущностью, на основе которой строится работа с входными и выходными данными, является класс Matrix. В данном классе существуют методы, определяющие подготовительную работу алгоритма и выполняющие перестановку матрицы. Объекты данного класса необходимы для работы со структурными матрицами. Поля и методы класса Matrix приведены в листинге 1.
Листинг 1. Класс Matrix
|
public class Matrix { public static int rows; //число строк public static int cols; //число столбцов public static int [,] A; //структурная матрица public Matrix(int row, int column){…}// конструктор public int this [int row, int column]{…}//индексатор public void Fill(){…}//Заполнение матрицы из файла public int [,] Displacement(int [] pi) //применение перестановки, pi- вектор перестановки
private static List
private static List
public List
public static D FindD(List
public void Print(){…} //печать матрицы в консоль } |
Следуя принципу ООП — декомпозиции [4], были созданы структуры, отвечающие за основные элементы в работе алгоритма, такие как:
− множество D (D);
− элемент множества возможных продолжений (PossibleExtension);
− центральный элемент (CentralElement);
− весовой коэффициент (WeightCoefficient);
− упорядоченное множество (OrderedMultitude).
В каждой структуре существует конструктор. В большинстве структур представлены методы, связанные с поиском нужных элементов. Структуры и их методы представлены в Листинге 2.
Листинг 2 . Класс Matrix
|
public struct D {
public List
public List
public List
public D(List
} public struct PossibleExtension { public int i; public int j; public int weight;
public List
public PossibleExtension(int _i, int _j, int _weight, List
public static List
public static PossibleExtension FindKnot(List
} public struct CentralElement { public int index; public int weight; public CentralElement(int _index, int _weight){…}
public static CentralElement FindCentral(List
} public struct WeightCoefficient { public int index; public int weight; public WeightCoefficient(int _index, int _weight){…} } public struct OrderedMultitude { public int weight;
public List
public OrderedMultitude(int _weight, List
} |
Анализ результатов работы.
После завершения тестирования алгоритма был проведен анализ работы программы на задаче 2. Анализ производился при помощи встроенных инструментов Visual Studio. Затраты ресурсов памяти проверялись при помощи Visual Studio Diagnostic Tools [5], а времени при помощи System.Diagnostics.Stopwatch [6].
В ходе анализа работы программы была выявлена зависимость ресурсов от размерности при фиксированной плотности и от плотности при фиксированной размерности.
Для тестирования зависимости параметров работы программы от плотности были случайным образом сгенерированы по 10 случайных структурных матриц размерности 10×10 с фиксированной плотностью и брались средние результаты затрат памяти и времени. Таким образом была получена данная зависимость.
Для демонстрации результатов была выбрана логарифмическая шкала, из-за удобства отображения в ней больших диапазонов значений величин. Для этого время (t) переведено в мс., а память (w) в Мб, затем данные значения прологарифмированы по основанию 2. Результаты представлены на рис. (1), (2).
Стоит отметить, что самой ресурсозатратной оказалась плотность 0,2. Это связано с тем, что при такой плотности граф является слабосвязным, работа алгоритма не завершается за один проход алгоритма и существует большое количество перспективных перестановок.
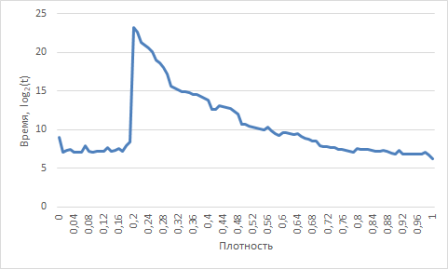
Рис. 1. Зависимость времени от плотности
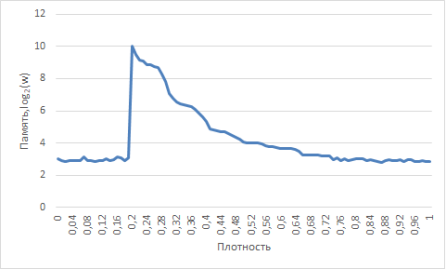
Рис. 2. Зависимость памяти от плотности
При тестировании зависимости параметров работы программы от размерности, при фиксированной плотности были сгенерированы матрицы размерностями от 10 до 25 включительно. Данный процесс был повторен для плотностей с 0,35 до 0,65 включительно с шагом 0,5. В связи с тем, что разброс результатов оказался невелик, результаты представлены без преобразований, время (t) в секундах и память (w) в Мб. Результаты работы продемонстрированы на рис. (3), (4).
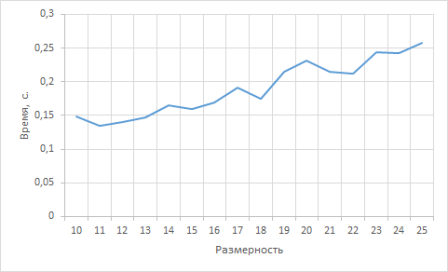
Рис. 3. Зависимость времени от размерности
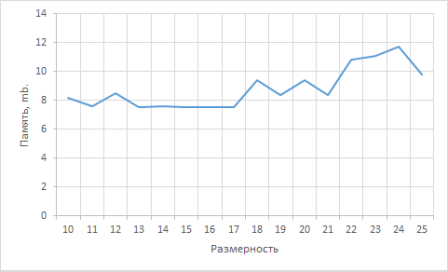
Рис. 4. Зависимость памяти от размерности
Литература:
- Олемской И. В. Явный метод типа Рунге — Кутты пятого порядка // ЖВТ. 2005. № 2.
- Олемской И. В. Модификация алгоритма выделения структурных особенностей // Вестник СПбГУ. Серия 10. Прикладная математика. Информатика. Процессы управления. 2006. № 2.
- C#: требования и рекомендации по написанию кода. https://habr\\.com/ru/post/26077/
- Luca Cardelli, Peter Wegner. On Understanding Types, Data Abstraction, and Polymorphism // ACM Computing Surveys. — New York, USA: ACM, 1985. — Vol. 17, n. 4 — pp 471–522 — ISSN 0360–0300.
- Measure memory usage in Visual Studio. https://docs.microsoft.com/en-us/visualstudio/profiling/memory-usage?view=vs-2019
- Class Stopwatch. https://docs.microsoft.com/en-us/dotnet/api/system\\.diagnostics.stopwatch?view=netcore-3.1







