На сегодняшний день одна из основных причин смертности — рак. Ученые во всем мире борются за прогресс в понимании природы этого заболевания и ищут способы лечения. Диагностика рака производится с помощью гистологического анализа. Анализ основан на методах изучения ткани по ее двумерным срезам. Однако, существует предположение, что причина болезни может быть не в отдельно взятой клетке, а в структуре клеточной ткани. Изучение трёхмерной структуры биологической ткани новая развивающаяся область гистологии. Основная идея — построение множества моделей ткани. В настоящее время не существует удобного программного обеспечения, облегчающего данный процесс. В данной работе в рамках существующего программного обеспечения для трехмерного моделирования тканей животных и человека разработан и реализован алгоритм определения топологии биологической ткани по начальному срезу и создан механизм построения соответствующей ему трёхмерной модели. Разрабатываемое программное обеспечение призвано помочь гистологам в задачах изучения структуры тканей животных и человека.
Ключевые слова: гистология, трехмерное моделирование, клетка, биологическая ткань, топологический примитив.
Введение
По данным Всемирной Организации Здравоохранения рак — одна из основных причин смертности в мире [1]. Ученые борются за прогресс в понимании природы этого заболевания и в поиске его лечения, но единого лекарства, которое бы подходило для каждого человека все еще не найдено. Точная диагностика данного заболевания производится с помощью гистологического анализа. Процедура заключается в изучении специально подготовленных тончайших срезов тканей под микроскопом, то есть метод основан на анализе двумерной структуры тканей.
Однако существует предположение, что при таких патологиях, как раковые опухоли, видоизменяются не отдельно взятые клетки, а их расположение друг относительно друга в пространстве. Трехмерный подход к изучению тканей основывается на их экстра- и интерполяции, что позволяет судить о форме и смежности клеток даже на тех уровнях, которые не были исследованы экспериментально. Изучать трехмерную структуру тканей экспериментальным путем достаточно сложно, поэтому актуальной является задача разработки программного обеспечения, позволяющего моделировать и визуализировать трехмерное строение тканей по их двумерному срезу.
В данной работе описывается процесс разработки алгоритма определения топологии ткани по начальному срезу путем внедрения новых клеток в имеющуюся топологию клеточного слоя. Данный алгоритм является основой механизма построения трехмерной модели клеток по начальному двумерному срезу биологической ткани. Разработка производится в рамках существующего программного обеспечения, основанного на теории трехмерной структуры биологической ткани Савостьянова Г. А. [2], позволяющего строить и исследовать различные модели пространственной организации клеток.
Описание алгоритма
Основной задачей программного обеспечения, основанного на теории трёхмерного строения ткани Савостьянова Г. А., является построение множества допустимых моделей ткани. Существует несколько подходов к этому процессу. В рамках данной работы рассмотрим один из них. Основой данного похода является преобразование начального среза биологической ткани путем внедрения в его топологию новых клеток. Рассмотрим идею алгоритма внедрения новых клеток в топологию слоя ткани на основе данного подхода.
- Выбирается в качестве исходной какая-либо двумерная мозаика из 11 вариантов, совпадающих с Платоновыми и Архимедовыми паркетами [3], построенных для однослойных эпителиев (удобно начинать с простых мозаик, то есть из клеток с минимальной смежностью и постепенно переходить к клеткам с большей смежностью).
- Выбираются точки внедрения новых клеток.
- Основываясь на принципе сохранения междугранных углов, правиле равномерности изменения клеточных граней и некоторых топологических преобразованиях, постепенно уменьшается площадь клеток какого-либо типа путем изменения размеров и числа их граней.
- Согласно теории, освобождающееся место будет занято клетками другого типа, при этом площадь пласта не изменяется (такое внедрение может происходить как в вершины, так и в грани клеток).
- По множеству сечений восстанавливается форма и взаиморасположение клеток в пространстве — строятся трёхмерные модели, отражающие топологию пласта и геометрию составляющих его клеток.
- Проводится верификация построенной модели — сравниваются срезы реальных тканей с теоретическими сечениями моделей, то есть ищутся предсказываемые структуры, которые в наибольшей степени соответствуют реальности.
Формализация алгоритма
Каждому срезу ткани можно сопоставить граф, в котором вершины соответствуют клетками. Если две клетки имеют общее ребро на срезе, то соответствующие вершины соединены ребром. Такой граф — топологический граф среза — полностью отражает топологию ткани на данном срезе. При начальном изменении топологии среза, то есть добавлении новых клеток в вершины / ребра, получается новый граф.
Суть алгоритма определения топологии по начальному срезу сводится к поиску в раскрашенном (черные — вершины, которые были изначально, белые — добавлены в процессе изменения топологии) планарном графе подграфов, изоморфных данному (то есть поиск некоторых топологических примитивов) и замены их на другие примитивы.
В данном случае решается не общая задача, потому что имеется конечный набор топологических примитивов (графов), которым надо найти изоморфные подграфы. В каждом конкретном случае заранее известно, какие именно подграфы надо искать (это зависит от изменения топологии — куда именно была проведена вставка новых клеток: в вершины / в щели). Для поиска в графе изоморфных топологическим примитивам подграфов существуют определённые полиномиальные алгоритмы. Рассмотрим один из них.
Алгоритм поиска топологического примитива № 1:
- Перебираем в графе ребра, соединяющие две черные вершины. Найденное ребро — e .
- Сортируем инцидентные черным вершинам ребра по углу с e.
- Две черные вершины инцидентные е назовём v1, v2 . Находим самое левое и правое ребра относительно е, если:
– они инцидентны v1, v2 соответственно и при этом инцидентны одной вершине (пусть v3 )
– они инцидентны v2, v1 соответственно и при этом инцидентны одной вершине (пусть v4 )
– То подграф, образуемый вершинами v1, v2, v3, v4 изоморфен графу, соответствующему топологическому примитиву № 1.
- Ребро (v1, v2) может быть заменено в исходном графе на ребро (v3, v4), то есть удаляем первое, вставляем второе.
- Повторяем шаги 2–4 для всех найденных ребер в шаге 1.
Временная оценка алгоритма:
- Перебор вершин — O(N).
-
Сортировка вершин —
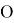
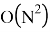
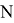
Следовательно, временная сложность алгоритма в общем случае —
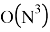
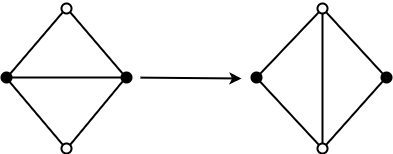
Рис. 1. Изменение топологии согласно алгоритму поиска топологического примитива № 1
Описание имплементации разработанных алгоритмов
В контексте программы связи между клетками — являются линиями, клетки — точками. Начальная и конечная точка связи соответствует какой-либо клетке в зависимости от топологии. Внедрение клеток пользователем построено таким образом, что нет возможности внедрить клетку в место, где её не может быть исходя из топологии начального среза ткани. В практическом смысле это ограничение не позволяет разрывать клетку изнутри. Далее приведены примеры реализации алгоритмов в программе.
Алгоритм поиска топологического примитива № 1:
- Для всех внедренных клеток находим порожденные ими новые связи.
- Из внедренных клеток выбираются те, которые связаны общем ребром, существовавшим до внесения изменений в топологию слоя. Это и есть топологический примитив № 1.
- Координаты внедрённых клеток преобразуются в координаты топологии слоя. Это необходимо, поскольку внедрение происходит кликом мыши в желаемую точку.
- Среди связей, существовавших до внедрения новых клеток, находятся такие, что находятся внутри найденного топологического примитива и удаляются.
- Добавляется новая связь внутри топологического примитива для внедрённых клеток.
Алгоритм поиска топологического примитива № 3:
- Из всех связей пласта выбираются такие, у которых одна из точек совпадет с внедренной клеткой.
- На основе найденных связей на шаге 1, выбираются клетки, которые имеют 3 связи из найденных и при этом каждая из связей оканчивается во внедренной клетке.
- Находятся связи, соответствующие найденным на шаге 2, клеткам и удаляются.
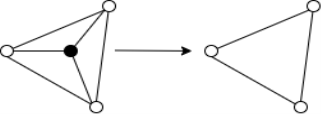
Рис. 2. Изменение топологии согласно алгоритму поиска топологического примитива № 3
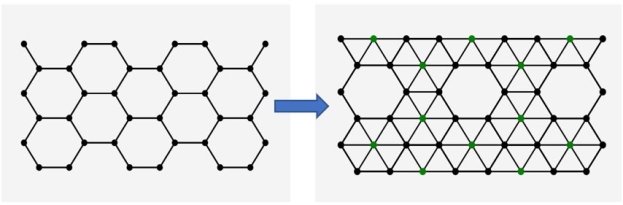
Рис. 3. Процесс внесения точек в начальную топологию пласта (результат работы программы)
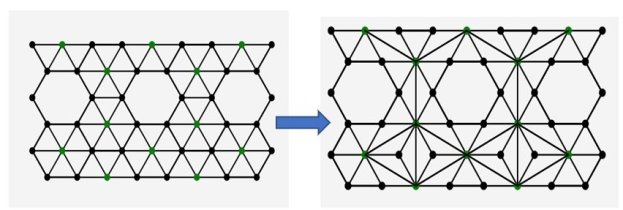
Рис. 4. Преобразование топологического примитива № 1 (результат работы программы)
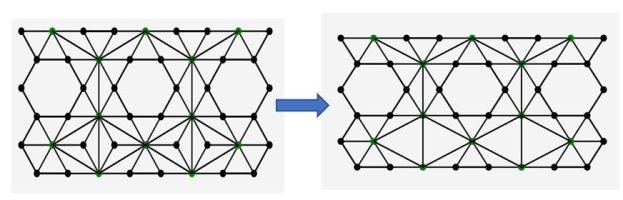
Рис. 5. Преобразование топологического примитива № 3 (результат работы программы)
Выводы
В рамках данной работы разработан алгоритм определения топологии биологической ткани по начальному срезу путем внедрения новых клеток в топологию среза. Данный алгоритм реализован в рамках существующего программного обеспечения, позволяющего строить и исследовать различные модели пространственной организации клеток. Алгоритм является основой для автоматизации процесса трехмерного моделирования структуры ткани путем внедрения новых клеток в топологию начального среза, что является актуальной задачей.
Литература:
- Cancer. — Текст: электронный // World Health Organization: [сайт]. — URL: https://www.who.int/news-room/fact-sheets/detail/cancer (дата обращения: 28.06.2020).
- Савостьянов, Г. А. Основы структурной гистологии. Пространственная организация эпителиев / Г. А. Савостьянов. — СПб: Наука, 2005. — 275 c. — Текст: непосредственный.
- Михайлов, О. В. Одиннадцать правильных паркетов / О. В. Михайлов. — Текст: непосредственный // Квант. — 1979. — № 2. — С. 9–14.







