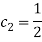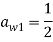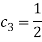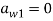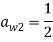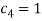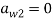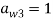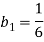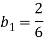Статья посвящена нахождению приемов и способов улучшения и оптимизации известных методов интегрирования систем обыкновенных дифференциальных уравнений (СОДУ). Задача уменьшения вычислительной погрешности при меньших затратах является наиболее актуальной для всех численных методов. В статье подробно рассматривается применение метода компенсированного суммирования для явного метода Рунге — Кутты четвертого порядка.
Ключевые слова: система обыкновенных дифференциальных уравнений, компенсированное суммирование, алгоритм Гилла — Мёллера, методы Рунге — Кутты.
Двадцать первый век можно охарактеризовать как период, в течение которого классические методы решения обыкновенных дифференциальных уравнений (ОДУ), таких как методы Рунге — Кутты, разработанные для ручного счета, развивались исходя из требований и цифровых возможностей. Однако в практических вычислениях природа компьютерной арифметики может играть значительную и, возможно, подавляющую роль.
Алгоритм Гилла — Мёллера
В книге Бутчера [1] представлен анализ влияния ошибки округления в явном методе Эйлера, а также приведен алгоритм Гилла — Мёллера (Гилл [2], Мёллер [4], [5]), который называют «компенсированным суммированием». В данном разделе будет проведен аналогичный численный эксперимент для преодоления последствий накопления ошибок округления в явном методе Рунге —Кутты 4-го порядка.
Пусть
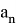
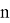
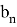
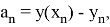
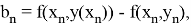
последовательности точных и приближённых значений связаны между собой следующим образом
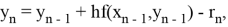
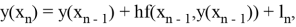
где
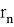
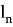
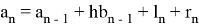
Так как, детальный анализ ошибки округления в расчетах данной задачи представлен в работе Хенричи [3], то вместо того, чтобы пытаться провести анализ
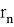
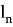
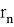
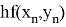
Этот усовершенствованный метод, который может быть использован для многих ситуаций, связанных с суммированием большого количества малых величин, и называют алгоритмом Гилла — Мёллера или «компенсированным суммированием».
« Компенсированное суммирование » в явном методе Рунге — Кутты 4-го порядка
Общая схема явного метода Рунге — Кутты (ЯМРК) численного интегрирования СОДУ
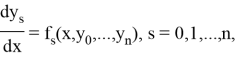
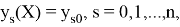
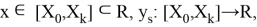
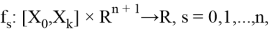
выглядит следующим образом:
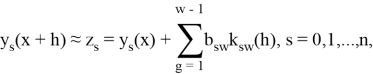
где функции
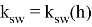
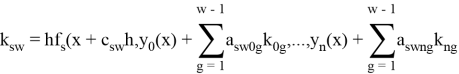
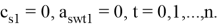
Здесь
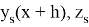
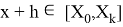
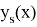
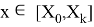
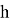
Традиционным считается символически представлять данный метод посредством таблиц Бутчера. Приведем пример таблицы Бутчера для ЯМРК 4-го порядка.
|
0 |
||||
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Далее будет показано как применить «компенсированное суммирование» для уменьшения ошибки округления в ЯМРК четвертого порядка на примере системы дифференциальных уравнений
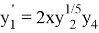
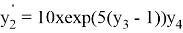
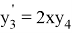
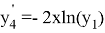
с начальным приближением
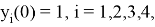
которое имеет аналитическое решение
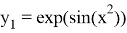
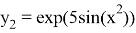
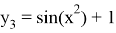
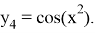
Реализация данного метода была выполнена в системе научных вычислений MATLAB.
(ЯМРК4)

ЯМРК4 с компенсированным суммированием)

В данном примере была взята последовательность шагов
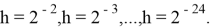
Результаты
Нанесем глобальные погрешности этих двух алгоритмов на один график в логарифмическом масштабе.
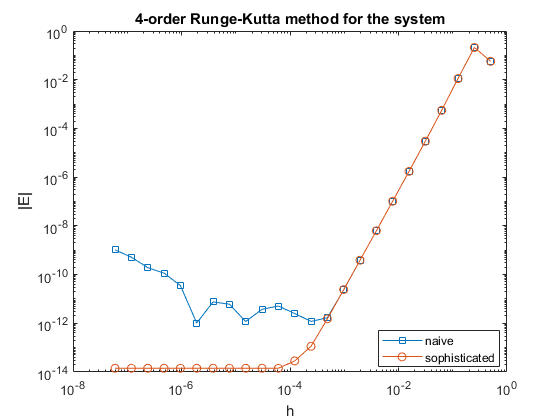
Видно, что явная форма дает результаты, которые сильнее ухудшаются при определенном шаге, в то время как компенсированная версия значительно улучшает результат.
Выводы
Как видно из проведенного исследования, метод «компенсированного суммирования» значительно улучшает ЯМРК четвертого порядка, а также его можно распространить и на другие численные методы интегрирования СОДУ.
Литература:
- Butcher J. C. «Numerical Methods for ordinary Differential Equations, Second Edition». The University of Auckland, New Zealand 2008, 463 p.
- Gill S. «A process for the step-by step integration of differential equations in an automatic computing machine». Proc. Cambridge Philos. Soc 1951.
- Henrici P. «Discrete Variable Methods in Ordinary Differential Equations». John Wiley & Sons Inc, New York 1962.
- Møller O. «Quasi double-precision in floating point addition». BIT 1965.
- Møller O. «Note on quasi double-precision». BIT 1965.