Кластерный анализ является одним из основных методов предварительной классификации большого количества информации. Актуальной задачей остаётся определение момента остановки процесса кластеризации. Можно рассмотреть кластерный анализ данных методом «одиночной связи» в виде дискретного случайного процесса и определить момент остановки с помощью квадратичных форм погрешности приближения «минимальных расстояний» функцией. В статье даётся определение «аппроксимационно-оценочным критериям». Применён один из критериев для кластеризации множества из 33 точек.
Ключевые слова: кластер, метод одиночной связи, аппроксимация, квадратичная форма, кластерный анализ.
Метод одиночной связи
Метод одиночной связи — иерархический агломеративный алгоритм, который выполняется в двумерном евклидовом пространстве со стандартной метрикой. За кластер мы берём центроиду всех точек, входящих в кластер, то есть изначально каждая точка является отдельным кластером, затем при увеличении кластера — средним арифметическим координат всех точек, входящих в кластер.
Итерации алгоритма можно описать следующим образом: на первом шаге необходимо определить расстояния между всеми n кластерами, построить множество минимальных расстояний, затем найти минимальное. Два кластера, расстояние между которыми минимально, объединяются, их центроида перевычисляется, получаем n-1 кластер [2]. Без остановки алгоритм в конечном итоге объединит все точки в один кластер, что является неудовлетворительным результатом.
Остановка процесса кластеризации
Множество минимальных расстояний является монотонно неубывающим, и при объединении больших кластеров испытывает «скачок». Например, для множества из 33 точек [2]
X={(0; 0); (2; 4); (3; 3); (1; 2); (3; 0); (3; 1); (1; 1); (12; 18); (13; 17); (11; 15); (13; 14); (14; 16); (11; 16); (12; 15); (13; 18); (12; 5); (13; 2); (14; 4); (12; 3); (13; 1); (14; 2); (24; 19); (22; 22); (21; 24); (23; 21); (24; 20); (22; 39); (23; 38); (24; 39); (21; 37); (2; 26); (24; 6); (10; 36)} график множества минимальных расстояний указан на рис.1.

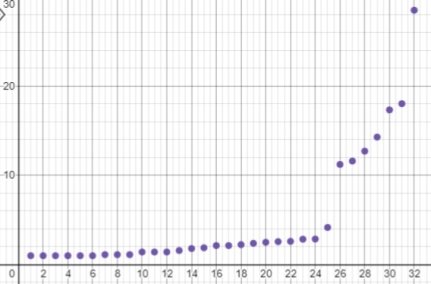
Рис. 1. Множество минимальных расстояний. На оси абсцисс указаны номера итераций, на оси ординат — расстояние между кластерами
Для того чтобы избежать проблемы объединения точек в один большой кластер, необходимо ввести критерий остановки. Будем приближать множество минимальных расстояний функцией для того, чтобы зафиксировать скачок (объединение кластеров). Хорошие результаты даёт приближение не всех точек сразу, а последовательно по 3 или 4 точкам. «Аппроксимационно-оценочные критерии» [1] являются квадратичными формами, оценивающими разность между квадратичной погрешностью линейной аппроксимации и квадратичной погрешностью одного из видов нелинейной аппроксимации (например, биквадратной — четвёртой степени). С вычислением критериев можно ознакомиться в работе [1]. Биквадратный аппроксимационно-оценочный критерий по четырём точкам имеет вид:
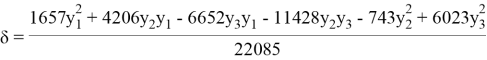
Здесь три переменные, но точек четыре. Это связано с введением упрощения:
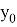
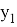
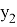
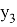
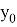
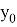
Результаты использования
Чувствительность критерия можно задать с помощью коэффициента q при линейном преобразовании
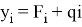
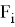
Для рассмотренного множества Х данный способ показывает хорошие результаты — при q от 0.18 до 0.63 процесс кластеризации методом одиночной связи заканчивается после 25 итерации (рис.2)

Рис. 2. Множество Х, разбитое на кластеры, после 25 итерации. Начало координат находится в левом верхнем углу
Выводы
Необходимо отметить, что рассмотренный критерий не единственный — можно вычислить экспоненциальный, квадратичный, кубический критерии. Они достаточно просты в использовании (но иногда сложны в вычислении), показывают хорошие и устойчивые результаты.
Литература:
- Орехов А. В. Аппроксимационно-оценочные критерии напряженно-деформируемого состояния твердого тела // Вестник Санкт-Петербургского университета. Прикладная математика. Информатика. Процессы управления. 2018. Т. 14. Вып. 3. С. 230–242. https://doi.org/10.21638/11702/spbu10.2018.304
- Орехов А. В. Марковский момент остановки агломеративного процесса кластеризации в евклидовом пространстве // Вестник Санкт-Петербургского университета. Прикладная математика. Информатика. Процессы управления. 2019. Т. 15. Вып. 1. С. 00–00.







