В исследовании рассмотрено применение мультиномиальной логистической регрессии при анализе уровня смертности от коронавируса. В работе приведены результаты построения модели, проведена интерпретация и оценка качества моделей. По результатам работы выявлены факторы, оказывающие влияние на целевую переменную.
Ключевые слова: регрессия, коронавирус, уровень смертности.
Мультиномиальные модели — это модели множественного выбора. Данный тип моделей применяется на наборах данных, содержащих некоторое количество объясняющих независимых переменных x и зависимую переменную y . Целевая переменная y является категориальной, она может являться номинальной или порядковой и имеет 3 и более альтернатив.
Допустим, в ходе эксперимента было проведено n наблюдений, в которых целевая переменная y i может принимать m различных значений. Вероятность того, что i -е наблюдение имеет класс j описывается формулой:
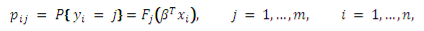
где F j — некоторая функция распределения, отвечающая условиям того, что вероятность p ij при фиксированном i принадлежит отрезку от 0 до 1, а в сумме такие вероятности дают 1.
В случае семейства логистических моделей, вместо функции F j используется логистическая функция распределения:
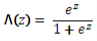
Можно выделить несколько типов мультиномиальных логистических моделей. Есть ряд особенностей, связанных с природой объясняющих переменных. В зависимости от них используют разные подвиды модели.
Если значение переменной x i не зависит от значения y i в рамках одного наблюдения, т. е. x i имеет одни и те же значения для каждого класса y i , то используется мультиномиальная логит модель:
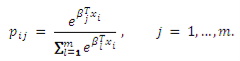
Поскольку сумма вероятностей p ij равна единице, то для определения модели накладывается условие β 1 =0 , если первая переменная выбрана базовой.
Данные для анализа уровня смертности от коронавируса собирались по всем 85 субъектам России из открытых источников, таких как Росстат, Роспотребнадзор и содержат такие показатели как: общее количество коек в больницах, количество коек в инфекционных палатах, врачей, общая смертность региона, население региона, его плотность, показатель валового регионального продукта, доля пенсионеров среди населения региона, количество аппаратов ИВЛ. Коэффициент смертности от коронавируса находится как отношение смертей от коронавируса к общей смертности субъекта РФ. Регионы были разбиты на 3 категории, с низким, средним и высоким уровнем смертности от коронавируса на равные группы.
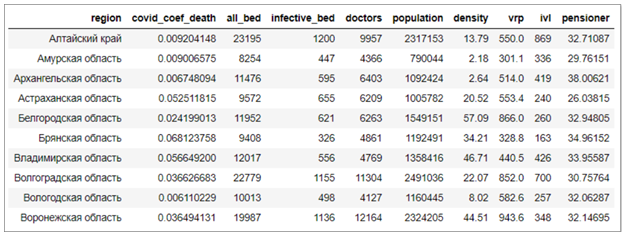
Одним из важных шагов при подготовке данных к построению регрессионных моделей, является проверка параметров на мультиколлинеарность. Для этого сначала построим корреляционную матрицу признаков. При абсолютных значениях коэффициента корреляции больше 0.8 связь между переменными считается сильной и использование таких параметров вместе может привести к плохому качеству модели, поэтому необходимо либо удалить такие переменные, либо преобразовать так, чтобы уменьшить корреляцию.
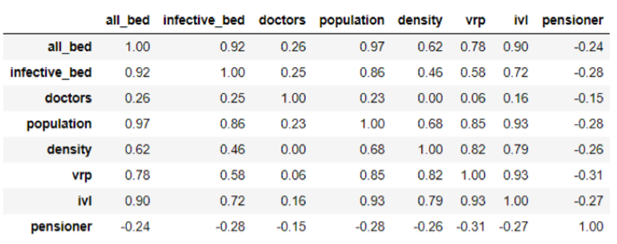
Из корреляционной матрицы можно сделать вывод, что в данных присутствуют коррелирующие величины.
Общее количество коек и количество коек в инфекционных палатах имеют сильную прямую зависимость, а значит не могут одновременно использоваться при построении моделей. Переменные ВРП региона и количество аппаратов ИВЛ также имеют сильную прямую зависимость с плотностью населения. Имеет смысл взять относительные показатели этих величин количество аппаратов ИВЛ на 100 тысяч населения и аналогичный параметр для ВРП. Переменная population имеет сильную корреляцию со многими другими параметрами, поэтому исключаем ее.
Проверку на мультиколлинеарность можно произвести с помощью коэффициента VIF (Variance Inflation Factor). Он показывает, во сколько раз возрастает дисперсия коэффициента регрессии из-за того, что переменные коррелируют по сравнению с тем, когда они не коррелируют. Если значение VIF > 5, то имеет место мультиколлинеарность. В данных не обнаружено мультиколлинеарности, значит, можно строить модели.
|
переменные |
VIF |
|
infective_bed |
1.4453 |
|
doctors |
1.1109 |
|
density |
1.3785 |
|
pensioner |
1.1829 |
|
ivl100 |
1.1244 |
|
vrp100 |
1.1095 |
Чтобы можно было оценить предсказательную мощность модели, разделим выборку на 2 части в пропорции 80/20: тренировочную, на которой модель будет обучаться, и тестовую, на которой будет выполняться проверка ее точности.
Было построено множество моделей, а с помощью метода обратного исключения последовательно удаляя из уравнения регрессии наименее значащие предикторы, получена наиболее оптимальная модель. Она также оказалась наилучшей по информационному критерию AIC и предсказательной способности на тестовых данных.
За базовый уровень был принят низкий уровень смертности. Для него все коэффициенты модели равняются нулю. А другие 2 уровня сравниваются с ним. Коэффициенты для высокого и среднего уровня смертности модели представлены в таблице ниже.
|
переменные |
high |
middle |
|
свободный член |
1.748946 |
1.495921 |
|
infective_bed |
-0.001229 |
-0.000832 |
|
density |
0.016465 |
0.015003 |
|
ivl100 |
-0.060092 |
-0.051951 |
Зададим уровень значимости 0.05. Тогда при p-value < 0.05 параметр модели значим. Согласно критерию отношения правдоподобия модель значима в целом, т. к. p-value = 0.017474, а значит такую модель можно использовать для предсказаний на тестовой выборке. Модель статистически значима в целом, ее коэффициенты значимы по критерию Вальда и проверка на тестовых данных дает хороший прогноз — 78.57 % правильных предсказаний.
Логарифмы отношения шансов для модели выглядят как:
− для низкого уровня смертности
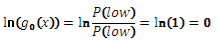
− для среднего уровня смертности
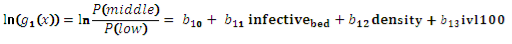
− для высокого уровня смертности

где b ij — коэффициенты модели, индекс i отвечает за класс (1- middle, 2 — high), j — за переменную, перед которой стоит коэффициент.
Чтобы получить значение вероятности выбора класса j = { low, middle, high }, необходимо перейти от логарифмов отношения шансов к выражению:
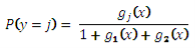
Интерпретация коэффициентов b ij моделей логистической регрессии такова: при изменении значения переменной x j на 1 единицу, при неизменных остальных значениях переменных, логарифм шансов изменяется в e bij раз.
В таблице представлены значения e bij для переменных.
|
своб. член |
infective_bed |
density |
ivl100 |
|
|
middle |
4.4634 |
0.9991 |
1.1511 |
0.9493 |
|
high |
5.7485 |
0.9987 |
1.0166 |
0.9416 |
Коэффициенты данной модели можно рассмотреть с точки зрения отношения шансов. При увеличении количества коек в инфекционных палатах на 1, при неизменных других факторах, шансы, что в регионе будет высокий уровень смертности по сравнению с низким, понижаются в 0.99 раз, т. е. значительное увеличение количества инфекционных коек может привести к снижению уровня смертности. Аналогично, увеличение коэффициента оснащения аппаратами ИВЛ также может способствовать небольшому снижению смертности в 0.94 раза.
Количество коек в инфекционных палатах является важным параметром при исследовании уровня смертности, т. к. вирус очень быстро распространяется и необходимо оперативно изолировать зараженных людей от здоровых, чтобы как можно меньше людей заболели, получили квалифицированную помощь и в случае осложнений, когда часто необходим аппарат ИВЛ, не скончались. Также можно отметить, что плотность населения играет немаловажную роль, наша страна обладает большой территорией и на разные регионы ложится разная нагрузка.
По итогам исследования выявлено, что наиболее сильное влияние оказывают такие параметры, как количество инфекционных палат, плотность населения, количество аппаратов искусственной вентиляции легких на 100 тысяч населения региона. В будущем можно увеличить количество факторов и выявить новые зависимости, влияющие на уровень смертности от коронавируса на территории Российской Федерации.
Литература:
- Long J. S. Regression models for categorical and limited dependent variables, Thousand Oaks: Sage Publ., 1997
- Cameron A. C., Pravin K. T. Microeconometrics: Methods and Applications, Cambridge University Press, 2005
- Fei, Yu Ting, Du Ronghui, Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study /Journal Title: The Lancet/2020
- Федеральная служба государственной статистики — URL: http://www.gks.ru/ — Текст: электронный.
- Роспотребнадзор — URL: https://rospotrebnadzor.ru/ — Текст: электронный.







