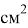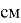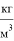Исследование зависимости времени затопления сосуда с отверстием в дне от параметров ёмкости



В статье описывается вариант теоретической модели затопления ёмкости с отверстием в дне и подтверждающие её практическими эксперименты. Приводятся результаты исследования зависимости времени затопления от параметров ёмкости.

Ключевые слова: время затопления, ёмкость с отверстием, саксонская миска.

В древности существовало множество различных способов измерения времени. Одним из уникальных вариантов является затопление сосуда с проделанным небольшим отверстием, через которое вода или другая жидкость медленно заполняет внутренность ёмкости. Этот способ использовался, например, саксами [2] для контроля длительности выступления оратора [1], [6]. Изучение этого явления важно, так как оно имеет практическое значение даже в наши дни. Наиболее значимы исследования этого явления в моделировании затопления судна. Однако некоторые из существующих закономерностей могут быть неточными из-за неучтённых законов и непроверенных эмпирически формул.

В своём исследовании мы решили уделить внимание частной задаче измерения времени с помощью сосуда. Мы рассматриваем ёмкости с прямыми (параллельными вектору погружения) тонкими стенками и перпендикулярным им (ровным) дном. Отверстие находится под центром тяжести сосуда. Выбор конкретного вида сосудов обусловлен исследованием общих закономерностей для подсчёта времени погружения: указанные характеристики позволяют использовать строгие теоретические законы.

Стоит отметить, что эта задача уже неоднократно решалась. Например, были исследованы следующие зависимости:

– время погружения обратно пропорционально квадрату диаметра круглого отверстия [1], [6]. Эта зависимость аналогична обратной пропорциональности между временем затопления ёмкости и площадью отверстия [4], [5];

– время погружения пропорционально радиусу круглого дна ёмкости [4]. Эта зависимость аналогична пропорциональности площади любого дна и времени затопления;

– время погружения обратно пропорционально корню из ускорения свободного падения [4], [5].

Однако на практике многократно была проверена только зависимость времени затопления от площади отверстия. Многие из зависимостей до сих пор носят исключительно теоретический характер. Именно поэтому эксперименты с этими водяными часами до сих пор актуальны.

Теоретическая модель

Для того чтобы теоретически описать погружение сосуда, я буду использовать следующие обозначения:

– — площадь дна сосуда, — площадь отверстия. В данном исследовании будет рассматриваться условие ;

– — масса сосуда;

– — высота сосуда;

– ,

— функции от времени, обозначающие высоту уровня жидкости, заполнившей сосуд, и глубину погружения (расстояние между уровнем жидкости вне сосуда и дном);

– — общая плотность ëмкости (сосуда): отношение массы к объëму, включающему пустоту внутри;

– — плотность жидкости;

– — время затопления ёмкости.

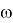
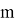
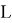
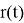
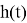
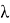
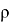
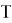
Рассмотрим силы, действующие на сосуд (рис. 1). Во-первых, на него действует сила со стороны воды, находящейся внутри сосуда, равная . Она параллельна вектору ускорения свободного падения. Во-вторых, на сосуд действует сила со стороны воды, находящейся под сосудом. Эта сила противоположна по направлению предыдущей и равна . В-третьих, на сосуд действует сила тяжести , направленная вниз. Необходимо заметить, что существуют и другие силы, действующие на ёмкость, но они или взаимно компенсируются (например, силы, действующие на стенки), или пренебрежимо малы (например, силы поверхностного натяжения), а потому их можно не учитывать.

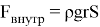
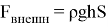
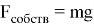
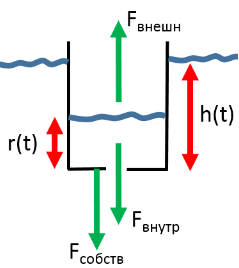
Рис. 1. Силы, действующие на сосуд во время погружения

Так как сосуд тонет медленно, можно допустить, что его ускорение равно нулю. Тогда из второго закона Ньютона можно получить равенство: . Оно преобразовывается в выражение: , откуда получаем: .

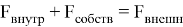
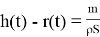
По формуле Торричелли для идеальной жидкости, обобщённой на случай затопленного отверстия [7, с. 362], получаем, что скорость жидкости, протекающей через отверстие в дне, равна: . Получается, что — константа, т. е. можно считать, что скорость жидкости, проходящей через отверстие в дне, постоянна и равна: .

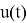
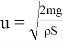
С одной стороны, за малый промежуток времени длительностью

в ёмкость добавляется объём жидкости, равный . С другой стороны, объём жидкости внутри сосуда изменяется на . Приравнивая эти выражения друг к другу и устремляя к нулю, получаем, что . Так как — константа, то, интегрируя, получаем: .

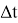
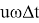
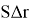
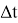
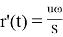
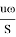
Пусть момент времени, в который ёмкость начинает тонуть, является нулевым, а спустя некоторое время сосуд затопляется. Так как , а , получаем:

, откуда .

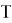
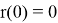
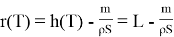
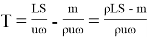
Используя величину , преобразовываем формулу для времени погружения:

.

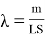
Таким образом, с помощью теоретической модели получаем формулу для времени затопления: . С её помощью мы обнаруживаем следующие зависимости:

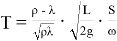
– время затопления пропорционально величине , где — плотность жидкости, в которой тонет сосуд, а

— плотность сосуда вместе с пустотой внутри;

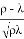
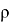
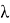
– время затопления пропорционально корню из высоты сосуда

– время затопления обратно пропорционально корню из ускорения свободного падения;

– время затопления пропорционально площади дна;

– время затопления обратно пропорционально площади отверстия в дне.

Эксперименты

Для подтверждения зависимостей, найденных с помощью теоретической модели, был проведён ряд экспериментов. В качестве ёмкостей использовались заглушки для труб, утяжелённые с помощью пластилина, (рис. 2) и жестяные крышки для банок (рис. 3).

Рис. 2. Заглушки для труб, используемые в качестве ёмкостей

Рис. 3. Жестяная крышка, используемая в качестве ёмкости

Для эксперимента использовалось следующее оборудование: ведро, пластиковая ёмкость, вода плотностью 1000 , масло плотностью 930 , соль (для получения солëной воды плотностью 1100 ), нож (ножницы) для проделывания отверстия, порционные весы, линейка, секундомер, набор заглушек для труб разных форм, крышки для консервных банок, два вида пластилина с разной плотностью.

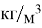
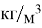
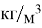
В каждом из экспериментов № 1–3 использовались 3 ёмкости (табл. 1) — крышки для консервных банок. Изучалась зависимость времени затопления от площади отверстия. В рамках эксперимента № 1 в качестве жидкости использовалась вода плотностью 1000 , для каждой ёмкости было проведено по 10 измерений; в рамках эксперимента № 2 в качестве жидкости использовалось масло плотностью 930 , для каждой ёмкости было проведено по 5 измерений; в рамках эксперимента № 3 в качестве жидкости использовалась солёная вода, имеющая плотность 1100 , для каждой ёмкости было проведено по 10 измерений.

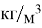
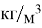
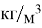
Таблица 1

Характеристики ёмкостей для экспериментов № 1–3

Номер ёмкости	,	,	,	,
1	82	1,3	21	0,09
2	82	1,3	21	0,32
3	82	1,3	21	0,60

На основе данных, полученных в эксперименте № 1 (табл. 2) и эксперименте № 3 (табл. 4), была подтверждена обратная пропорциональность между временем затопления и площадью отверстия в дне. На основе данных, полученных с помощью эксперимента № 2 (табл. 3), была обнаружена обратная пропорциональность между временем затопления и площадью отверстия, возведённой в степень 1.35, — .

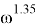
Отклонение от теоретической модели в случае с маслом объясняется использованием формулы Торричелли для идеальной жидкости. Так как масло обладает вязкостью, формула Торричелли должна быть посчитана с учётом дополнительных параметров [3, с. 206], [7, с. 362].

Таблица 2

Результаты эксперимента № 1

Номер ёмкости	,	,
1	60,5 ± 6,0	0,09
2	21,4 ± 1,1	0,32
3	10,4 ± 1,2	0,60

Таблица 3

Результаты эксперимента № 2

Номер ёмкости	,	,
1	153,4 ± 6,3	0,09
2	27,4 ± 1,0	0,32
3	12,0 ± 0,3	0,60

Таблица 4

Результаты эксперимента № 3

Номер ёмкости	,	,
1	67,7 ± 2,3	0,09
2	24,2 ± 1,3	0,32
3	11,9 ± 0,3	0,60

В экспериментах № 4–6 в качестве жидкости использовалась вода плотностью 1000

. В качестве ёмкостей использовались заглушки для труб. В рамках эксперимента № 4 для каждой из ёмкостей № 4–6 (табл. 5) проводились 10 измерений. На основе полученных данных (табл. 6) была подтверждена пропорциональность между временем затопления и площадью дна.

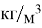
Таблица 5

Характеристики ёмкостей для эксперимента № 4

Номер ёмкости	,	,	,	,	,
4	9,6	3	19	0,196	660
5	15,2	3	30	0,196	658
6	22,9	3	45	0,196	655

Таблица 6

Результаты эксперимента № 4

Номер ёмкости	,	,
4	2,8 ± 0,3	9,6
5	5,0 ± 0,2	15,2
6	8,0 ± 0,4	22,9

В рамках эксперимента № 5 для каждой из ёмкостей № 7–9 (табл. 7) проводилось 5 измерений. На основе полученных данных (табл. 8) не была подтверждена пропорциональность между временем затопления и величиной , т. е. зависимость времени затопления от плотности ёмкости с внутренностью, полученная с помощью теоретической модели, является некорректной.

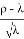
Таблица 7

Характеристики ёмкостей для эксперимента № 5

Номер ёмкости	,	,	,	,	,
7	102,0	3,8	65	0,196	168
8	102,0	3,8	80	0,196	206
9	102,0	3,8	110	0,196	284

Таблица 8

Результаты эксперимента № 5

Номер ёмкости	,	,
7	163,5 ± 4,0	64,2
8	123,0 ± 4,9	55,3
9	86,0 ± 1,3	42,5

В рамках эксперимента № 6 для каждой из ёмкостей № 9–10 (табл. 9) проводилось 5 измерений. На основе полученных данных (табл. 10) была подтверждена пропорциональность между временем затопления и корнем из высоты ёмкости.

Таблица 9

Характеристики ёмкостей для эксперимента № 6

Номер ёмкости	,	,	,	,	,
9	102,0	3,8	110	0,196	284
10	102,0	5,1	148	0,196	285

Таблица 10

Результаты эксперимента № 6

Номер ёмкости	,	,
9	86,0 ± 1,3	3,8
10	100,5 ± 1,1	5,1

Выводы

В рамках данного исследования были теоретически получены и эмпирически подтверждены следующие зависимости в случае с водой как используемой жидкостью:

– время затопления ёмкости обратно пропорционально площади отверстия в дне;

– время затопления ёмкости пропорционально площади дна в случае с небольшим относительно площади дна отверстием;

– время затопления ёмкости пропорционально корню из высоты сосуда.

В случае использования масла в качестве жидкости также была обнаружена зависимость:

– время затопления ёмкости обратно пропорционально площади отверстия, возведённой в степень 1.35 — .

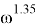
Кроме того, эмпирически опровергнута пропорциональность времени затопления и величины , где — плотность жидкости, в которой тонет сосуд, а — плотность сосуда вместе с пустотой внутри. Экспериментальная проверка обратной пропорциональности времени затопления и корня из ускорения свободного падения не проводилась.

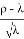
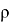
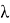
Заключение

Вопрос нахождения всех зависимостей между временем затопления ёмкости и её характеристиками остаётся открытым. Зависимости времени затопления сосуда от плотности ёмкости, плотности жидкости, а также от ускорения свободного падения до сих пор изучены недостаточно.

Литература:

1. Greer, A. An experiment with Saxon bowls / A. Greer, E. Kincanon // The Physics Teacher. — 2000. — № 38. — С. 112.

2. Replica of Saxon 'Sinking Bowl' Water Clock, 1931 // Science Museum Group: сайт. — URL: https://collection.sciencemuseumgroup.org.uk/objects/co530/replica-of-saxon-sinking-bowl-water-clock-1931-water-clock-replica (дата обращения: 30.06.20).

3. Савельев, И. В. Курс общей физики. Том 1. Механика, молекулярная физика. / И. В. Савельев. — М.: Наука, 1987. — 251 с.

4. Saxon Bowl IYPT 2020 — analytical solution from ilinblog (Саксонская миска) // Ilinblog: интернет-портал. — URL: http://ilinblog.ru/article.php?id_article=58 (дата обращения: 30.06.20). — Дата публикации: 25 июля 2019.

5. Алексеев, Г. М. Особые случаи морской практики: учеб. пособие / Г. М. Алексеев. — Морской транспорт, 1959. — 338 с.

6. Walding, R. New Century Senior Physics — Concepts in Context / R. Walding, G. Rapkins, G. Rossiter. — Oxford: Oxford University Press. — 2nd edition.

7. Зиновьев, В. А. Краткий технический справочник. Том 1. / В. А. Зиновьев. — М.: ГОСИЗДАТ, 1949. — 532 с.