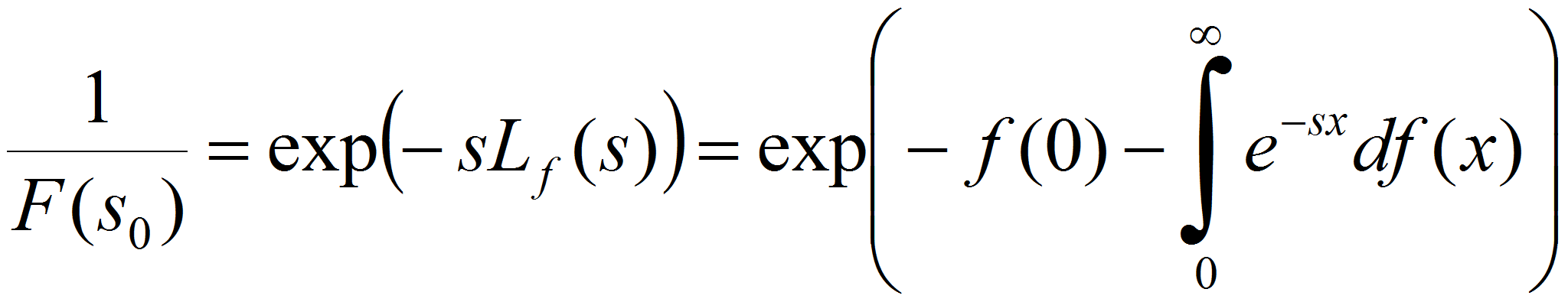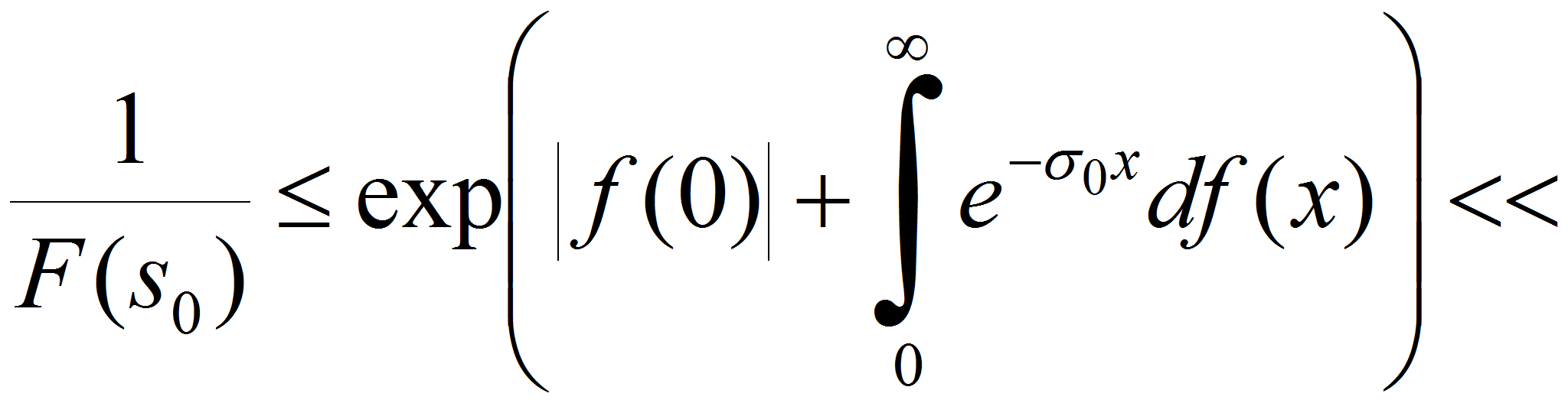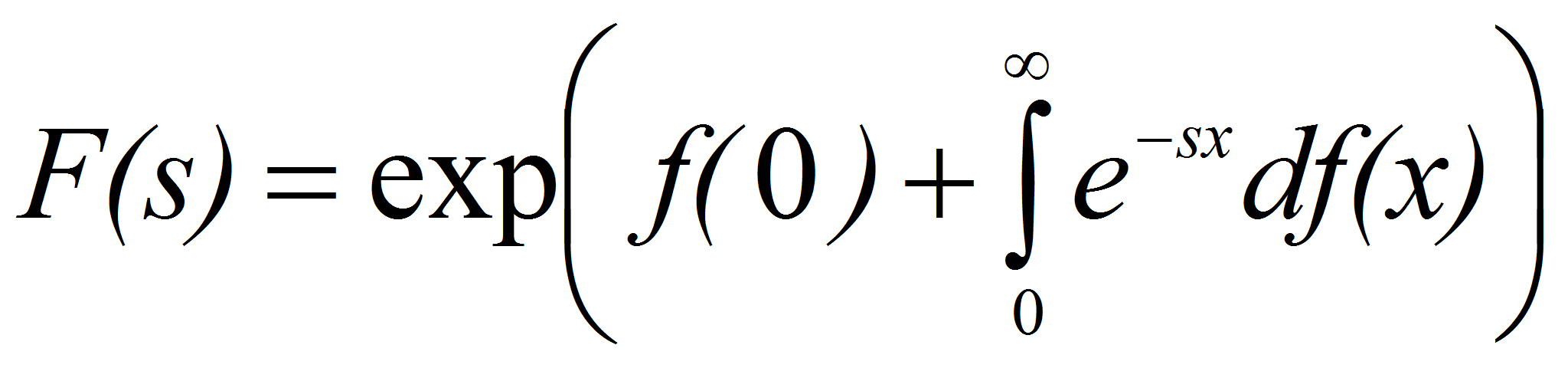В работе доказывается, что если полуплоскости сходимости преобразование Лапласа некоторой неубывающей функции близко к экспоненте преобразования Лапласа другой неубывающей функции и допускает аналитическое предложение в некоторую вертикальную полосу левее абсциссы сходимости, то оно не обращается в нуль в области, подобной области Валле-Пуссена, свободной от нулей дзета- функции.
In the work it is proved that if in a half plane of convergence the transformation of Laplasa of some nondecreasing function is close to an exponent of transformation of Laplasa of other nondecreasing function and supposes analytical continuation in some vertical strip more to the left of a convergence absciss thus it does not turn to zero in the area similar to area of Valle-Pussen free from zeta-function zero.
Классическая
постановка задачи о распределении простых чисел в натуральном ряду
состоит в исследовании асимптотического поведения функции
![]() означающий число простых чисел, не превосходящих
означающий число простых чисел, не превосходящих
![]()
Известные в настоящее время
асимптотические формулы для
![]() имеют вид
имеют вид
где
интегральный
логарифм, а
![]() - остаточный член, оценка которого связана с распределением нулей
дзета функции Римана:
- остаточный член, оценка которого связана с распределением нулей
дзета функции Римана:
Согласно теореме Валле-Пуссена
где
![]() - положительная константа.
- положительная константа.
Лучший из
известных в настоящее время результатов принадлежит Виноградову и
Коробову и состоит в том, что указатель
![]() можно заменить на
можно заменить на
![]() ,
где
,
где
![]() - произвольное малое положительное число. Первым шагом в
доказательстве этих оценок является классическое тождество Эйлера
- произвольное малое положительное число. Первым шагом в
доказательстве этих оценок является классическое тождество Эйлера
Используя элементарные сведения о простых числах из тождества Эйлера нетрудно получить, что
где
![]() - функция регулярное и ограниченная в полуплоскости
- функция регулярное и ограниченная в полуплоскости
![]()
С другой
стороны в полуплоскости с
![]()
и аналогично
введем обозначение
преобразование
Лапласа функции
![]() определенной для всех неотрицательных
определенной для всех неотрицательных
![]() и интегрируемой на каждом конечном отрезке
и интегрируемой на каждом конечном отрезке
![]()
Тогда из тождества Эйлера следует:
Таким
образом, задача о распределении простых чисел является частным
случаем следующей общей задачи: заданы две функции вещественного
аргумента
![]() и
и
![]() ,
преобразования Лапласа которых связаны соотношением (1), причем
функция
,
преобразования Лапласа которых связаны соотношением (1), причем
функция
![]() устроена достаточно хорошо.
устроена достаточно хорошо.
Считая
асимптотику функции
![]() известной, найти асимптотику функции
известной, найти асимптотику функции
![]() .
.
В
дальнейшем мы будем считать что при
![]()
где
![]() - положительная константа.
- положительная константа.
Отсюда следует, что преобразование Лапласа
абсолютно
сходится в полуплоскости
![]() .
.
При этом
для любого
![]() в полуплоскости
в полуплоскости
![]() сходимость равномерна и поэтому функция
сходимость равномерна и поэтому функция
![]() регулярна в полуплоскости
регулярна в полуплоскости
![]() .
.
Из формулы
(2) следует, что функция
![]() аналитически продолжается в полуплоскость
аналитически продолжается в полуплоскость
![]() ,
из которой удалена точка
,
из которой удалена точка
![]() в этой же точке функция
в этой же точке функция
![]() имеет простой полюс с вычетом равным
имеет простой полюс с вычетом равным
![]()
Действительно, так как
Из оценки
![]() непосредственно следует, что преобразование Лапласа
непосредственно следует, что преобразование Лапласа
![]() сходится абсолютно в полуплоскости
сходится абсолютно в полуплоскости
![]() и равномерно в полуплоскости
и равномерно в полуплоскости
![]() для любого
для любого
![]()
Отсюда
вытекает, что функция
![]() регулярна в полуплоскости
регулярна в полуплоскости
![]() .
.
В
дальнейшем мы полагаем
![]() так что
так что
![]()
Лемма
1.
Пусть
в условиях (1) и (2)
![]() неубывающая функция и
неубывающая функция и
![]() для
для
![]()
Тогда
функция
![]() не обращается в нуль на прямой
не обращается в нуль на прямой
![]() =
1.
=
1.
Доказательство. Введем обозначение
Тогда из (1) следует
Так как
то показатель степени равен
Поскольку
![]() для всех действительных
для всех действительных
![]() .
.
Таким
образом, если
![]() для действительных
для действительных
![]() то для любого действительного
то для любого действительного
![]()
С другой
стороны, пусть
![]() - нуль функции
- нуль функции
![]() кратности
кратности
![]() Тогда
Тогда
![]()
при
![]() Так как
Так как
![]() стремится к конечному пределу при
стремится к конечному пределу при
![]() и
и
![]() при
при
![]() ,
то
,
то
![]() т.е.
т.е.
![]() при
при
![]() в противоречии с неравенством (3). Лемма доказана.
в противоречии с неравенством (3). Лемма доказана.
Лемма
2.
Для
любого
![]() из условия (2) следует, что при
из условия (2) следует, что при
![]() справедливо оценка
справедливо оценка
Действительно,
Для дальнейшего нам понадобится следующие теоремы Ландау [1]
Теорема
А.
Пусть функция
![]() регулярна в круге
регулярна в круге
![]() и удовлетворяет в нём неравенству
и удовлетворяет в нём неравенству
Тогда
где
![]() - пробегает нули функции
- пробегает нули функции
![]() в круге
в круге
![]()
Теорема
B.
Пусть функция
![]() удовлетворяет условиям теоремы А и кроме того не обращается в нуль в
области
удовлетворяет условиям теоремы А и кроме того не обращается в нуль в
области
![]() где
где
![]() .
Тогда если
.
Тогда если
где
![]() - постоянная, то в круге
- постоянная, то в круге
![]() справедлива неравенство
справедлива неравенство
Применим
теорему A
к функции
![]() и кругу радиуса
и кругу радиуса
![]() с центром в точке
с центром в точке
![]() где
где
![]() такова, что точка
такова, что точка
![]() есть нуль функции
есть нуль функции
![]() причем
причем
![]()
Будем
считать, что
![]() тогда точка
тогда точка
![]() находится в круге
находится в круге
![]()
Из неравенства (5) следует
Откуда
Так как
функция
![]() не обращается в нуль в полуплоскости
не обращается в нуль в полуплоскости
![]() и
и
![]() ,
то все слагаемые последней суммы неотрицательные, и она может только
уменьшится если мы отбросим все слагаемые кроме одного в котором
,
то все слагаемые последней суммы неотрицательные, и она может только
уменьшится если мы отбросим все слагаемые кроме одного в котором
![]() Следовательно,
Следовательно,
Выясним
теперь, что в наших условиях можно взять в качестве
![]()
Так как
круг
![]() ввиду
ввиду
![]() находится от точки
находится от точки
![]() на расстоянии >2, то в этом круге по лемме 2.
на расстоянии >2, то в этом круге по лемме 2.
![]() и
и
(при
условии, что функция
![]() ограничена в полуплоскости
ограничена в полуплоскости
![]() ).
).
Далее
Откуда
Поэтому в
круге
![]() справедлива оценка
справедлива оценка
Следовательно,
функция
![]() в круге
в круге
![]() удовлетворяет условиям теоремы А при
удовлетворяет условиям теоремы А при
![]() где
где
![]() абсолютная константа.
абсолютная константа.
Поэтому из неравенства (6.8) следует
Применим теперь теорему А к той же функции
и кругу
радиуса
![]() с центром в точке
с центром в точке
![]() ,
где
,
где
![]() и
и
![]() определены так же, как и выше.
определены так же, как и выше.
Поскольку в неравенстве
где
![]()
![]() - пробегает нули функции
- пробегает нули функции
![]() в
в
круге
![]() все слагаемые суммы справа неотрицательны, то
все слагаемые суммы справа неотрицательны, то
Используя
лемму2. как и выше получаем, что в качестве
![]() можно взять величину
можно взять величину
![]() где
где
![]() абсолютная константа. Поэтому
абсолютная константа. Поэтому
Кроме того,
Откуда
следует, что функция
![]() имеет при
имеет при
![]() простой полюс с вычетом –1.
простой полюс с вычетом –1.
Следовательно,
при
![]() справедливо неравенство
справедливо неравенство
Отсюда и из предыдущих неравенств вытекает:
С другой
стороны, при
![]() ввиду равенства
ввиду равенства
имеем:
Откуда следует
так как
![]() - неубывающая функция. Сопоставляя это с неравенством (6.10),
получаем
- неубывающая функция. Сопоставляя это с неравенством (6.10),
получаем
До сих пор
![]() и
и
![]() - произвольные положительные числа с условием
- произвольные положительные числа с условием
![]()
Положим
теперь
![]() Тогда из предыдущего неравенства следует
Тогда из предыдущего неравенства следует
Пусть
![]() ,
тогда выражение в скобках положительно. Так как
,
тогда выражение в скобках положительно. Так как
![]() и
и
![]() то отсюда следует:
то отсюда следует:
Последнее
неравенство показывает, что
![]() где
где
![]() - положительная константа, зависящая только от
- положительная константа, зависящая только от
![]() .
Действительно, при достаточно малых
.
Действительно, при достаточно малых
![]() левая часть неравенства положительна, так как она стремиться к
левая часть неравенства положительна, так как она стремиться к
![]() ,
когда
,
когда
![]() Вспоминая определение
Вспоминая определение
![]() ,
получаем следующий результат:
,
получаем следующий результат:
Теорема
1.
Пусть
![]() и
и
![]() - функции определенные при
- функции определенные при
![]() причем
причем
![]() - неубывающая функция,
- неубывающая функция,
где
функция
![]() - такова, что
- такова, что
![]() ограничена в полуплоскости
ограничена в полуплоскости
![]() Тогда, если
Тогда, если
то функция
![]() не обращается в нуль в области
не обращается в нуль в области
где
![]() - положительная константа, зависящая только от
- положительная константа, зависящая только от
![]() .
.
Литература:
Landau E. Über den verlauf der zahlentheorethen Funktion. Arch. Math. und Phys. 5 (1903), 86-91.
Ингам А.Е. Распределение простых чисел.- ОНТИ, 1936.
Тичмарч Е. Теория дзета функции Римана, ИЛ, 1953.