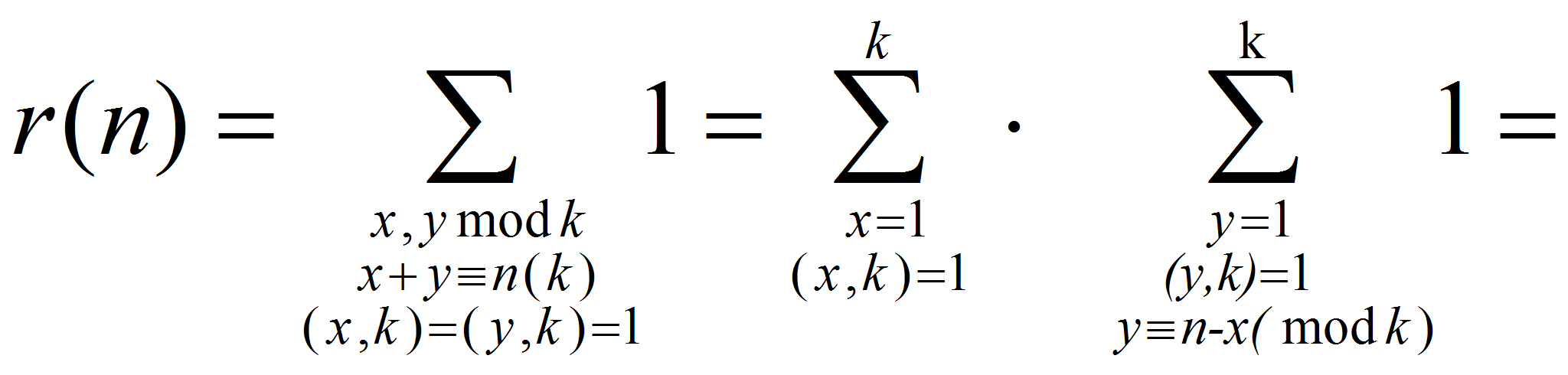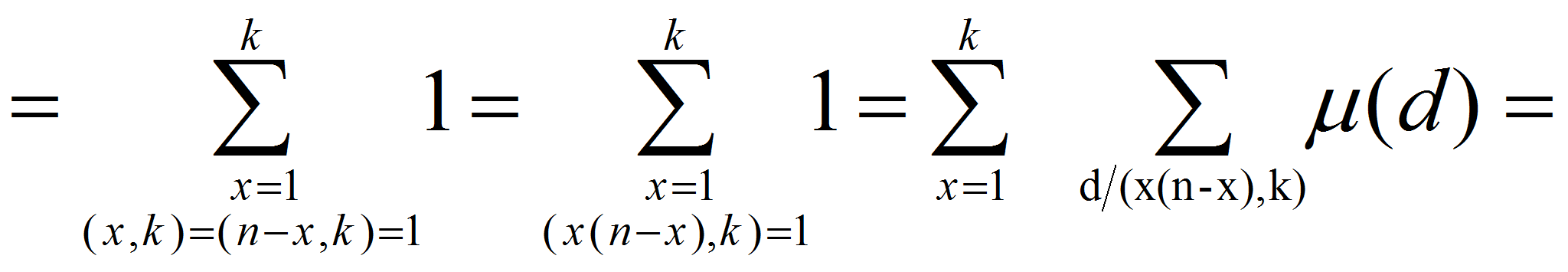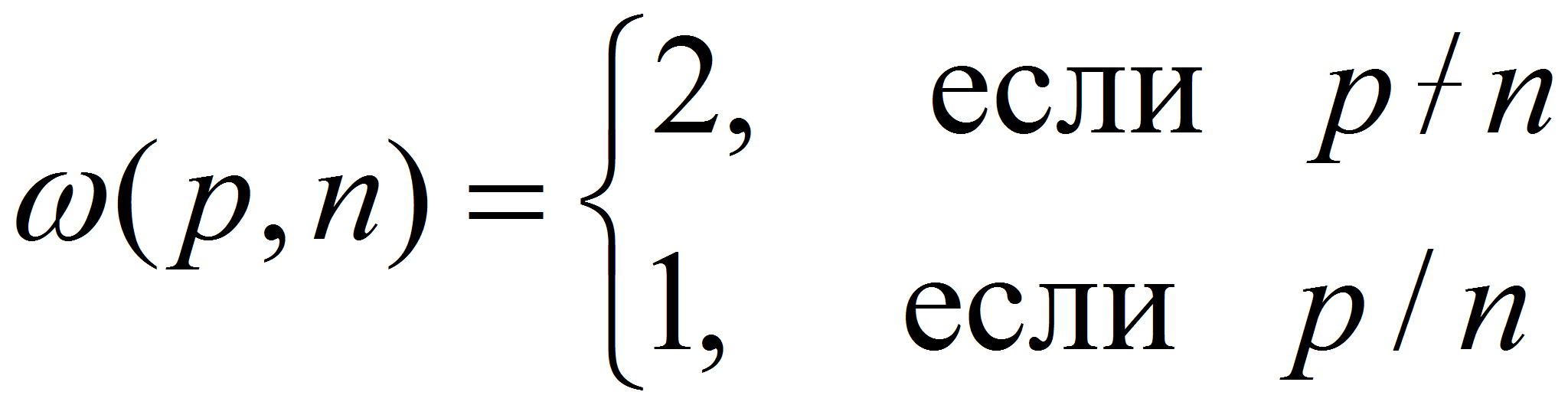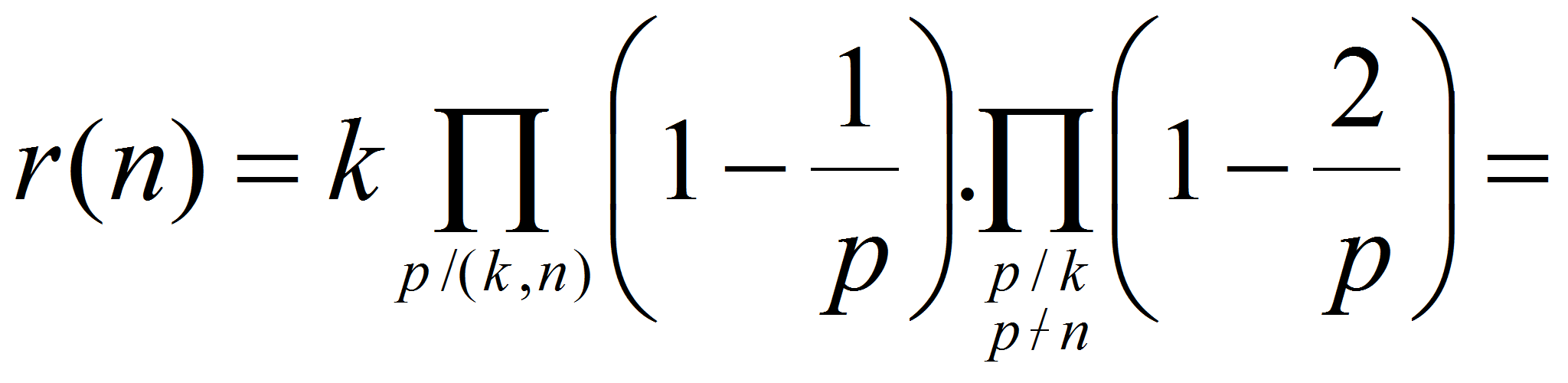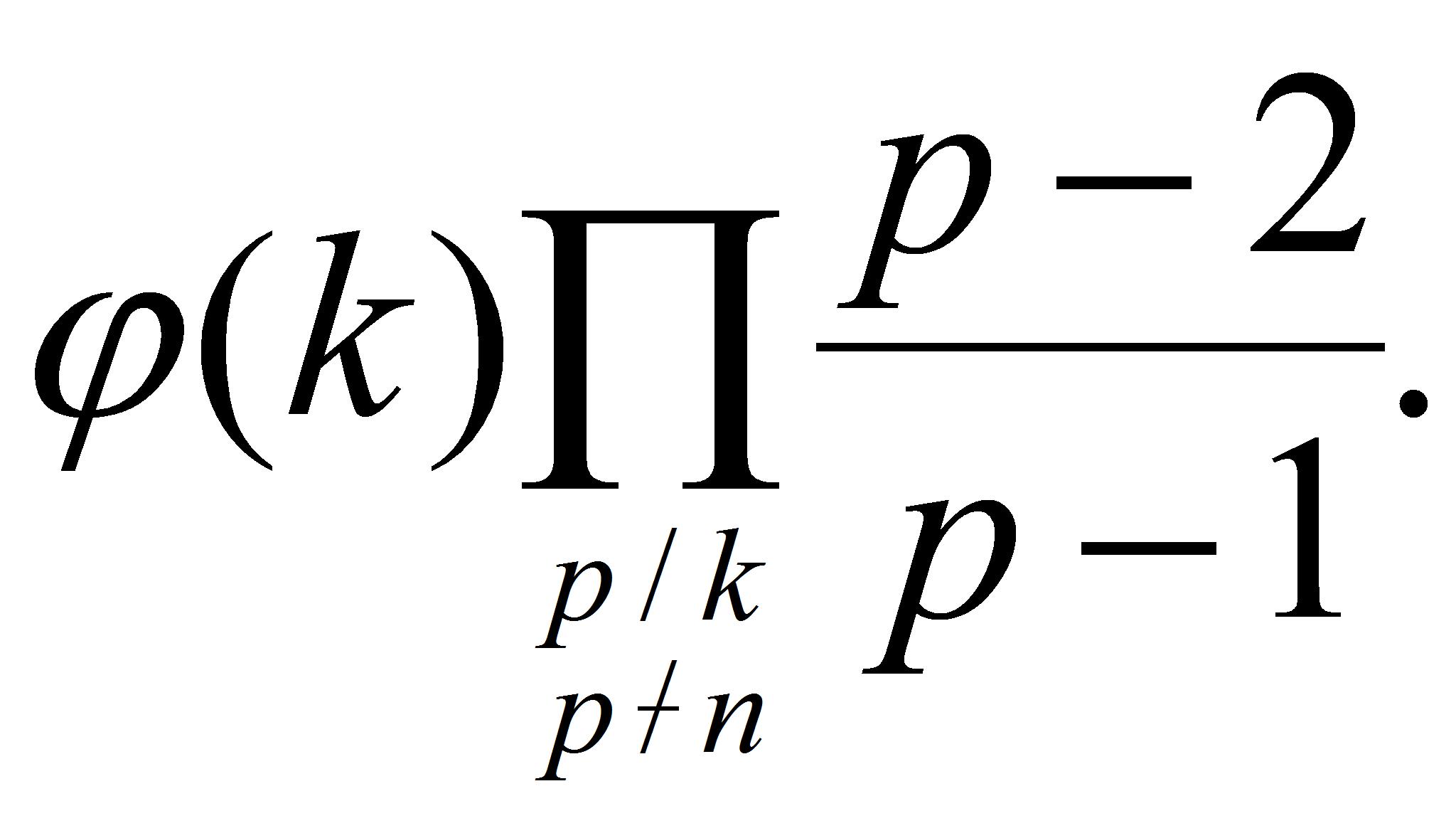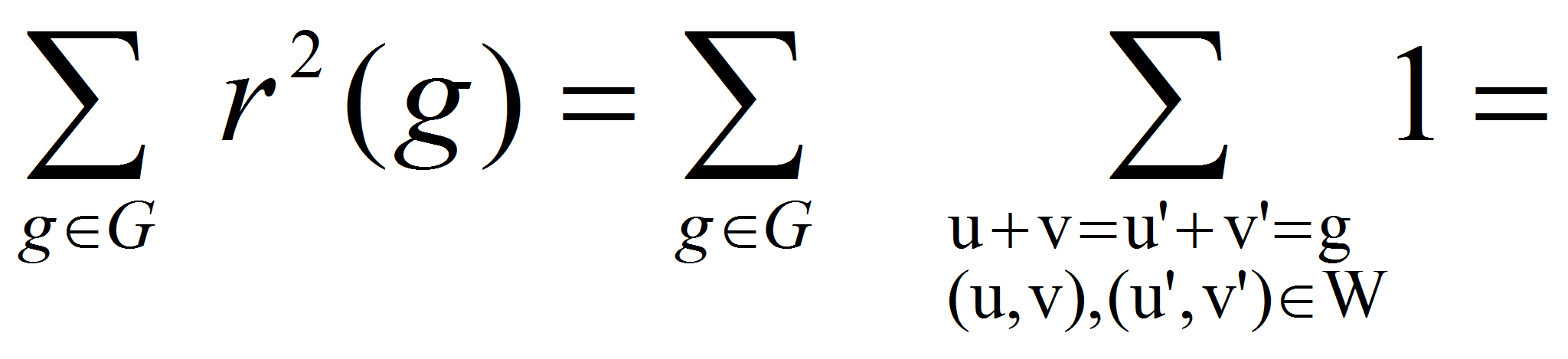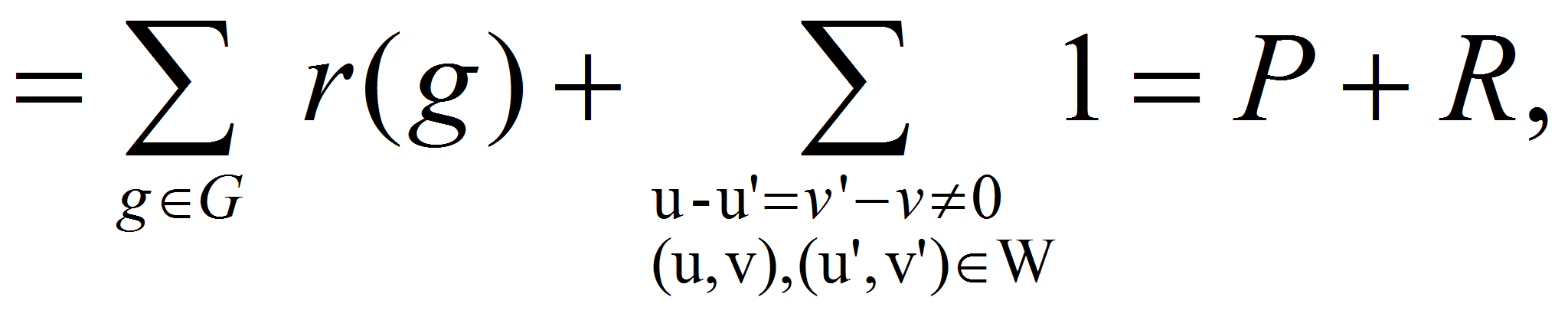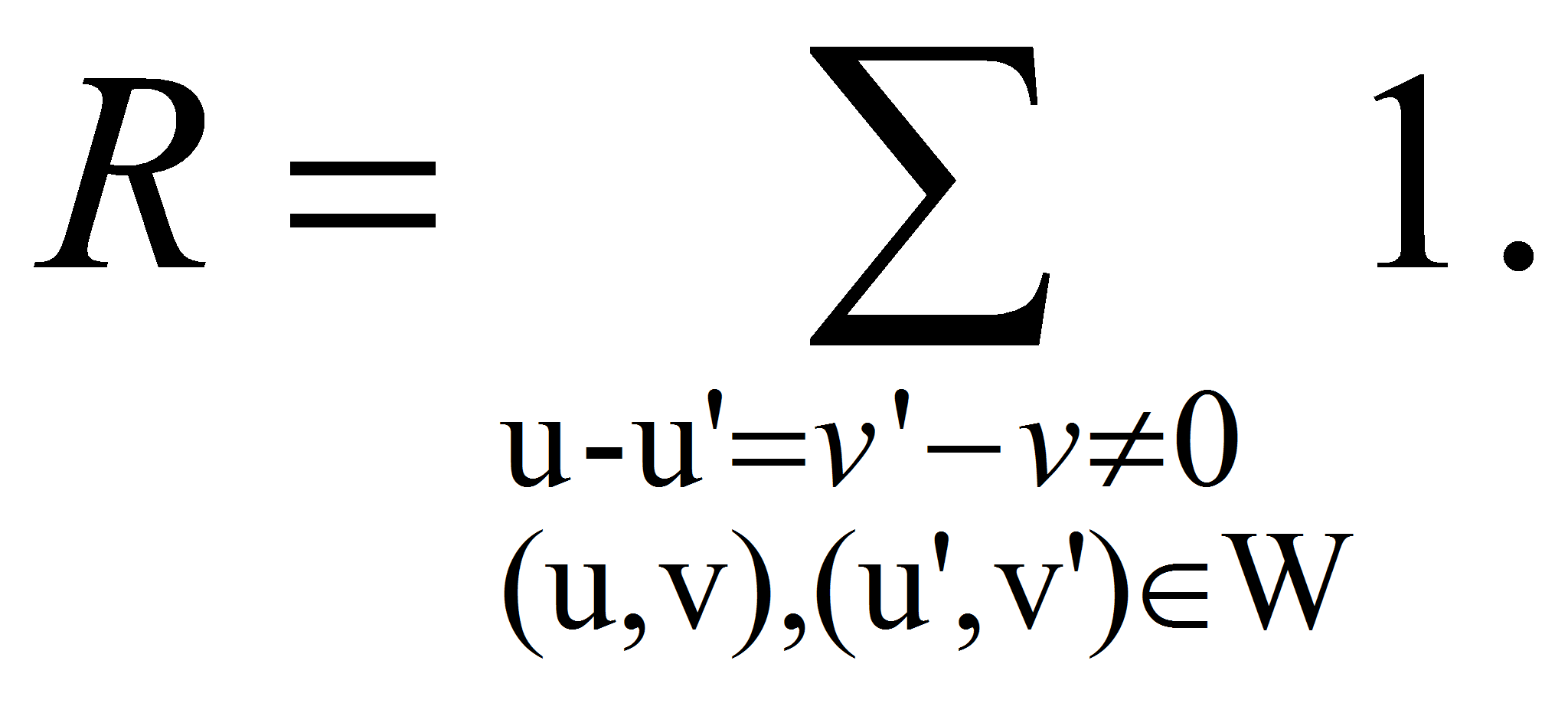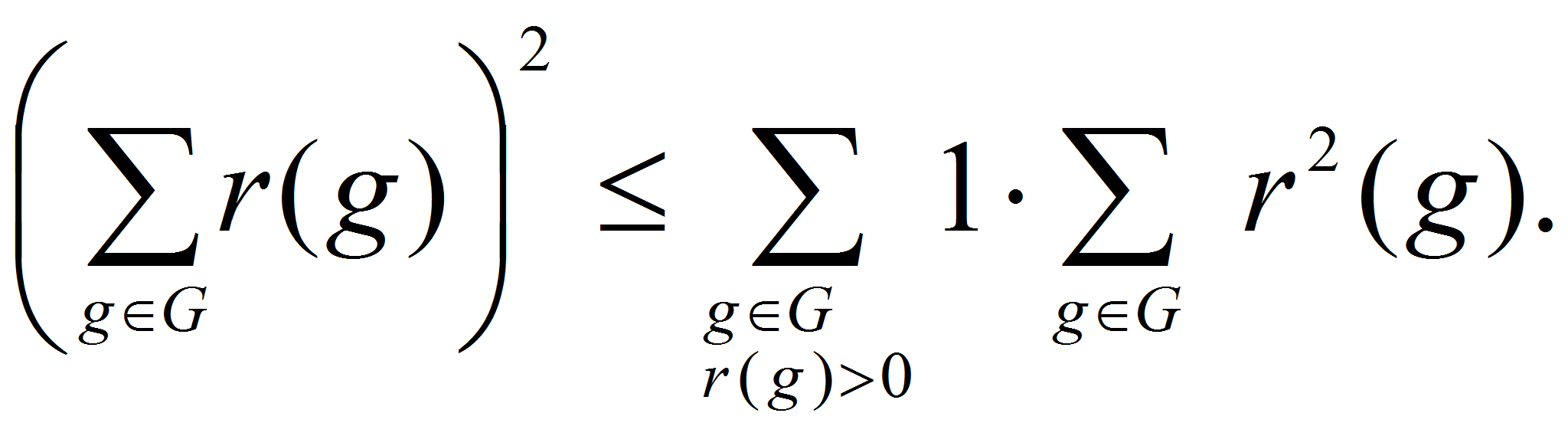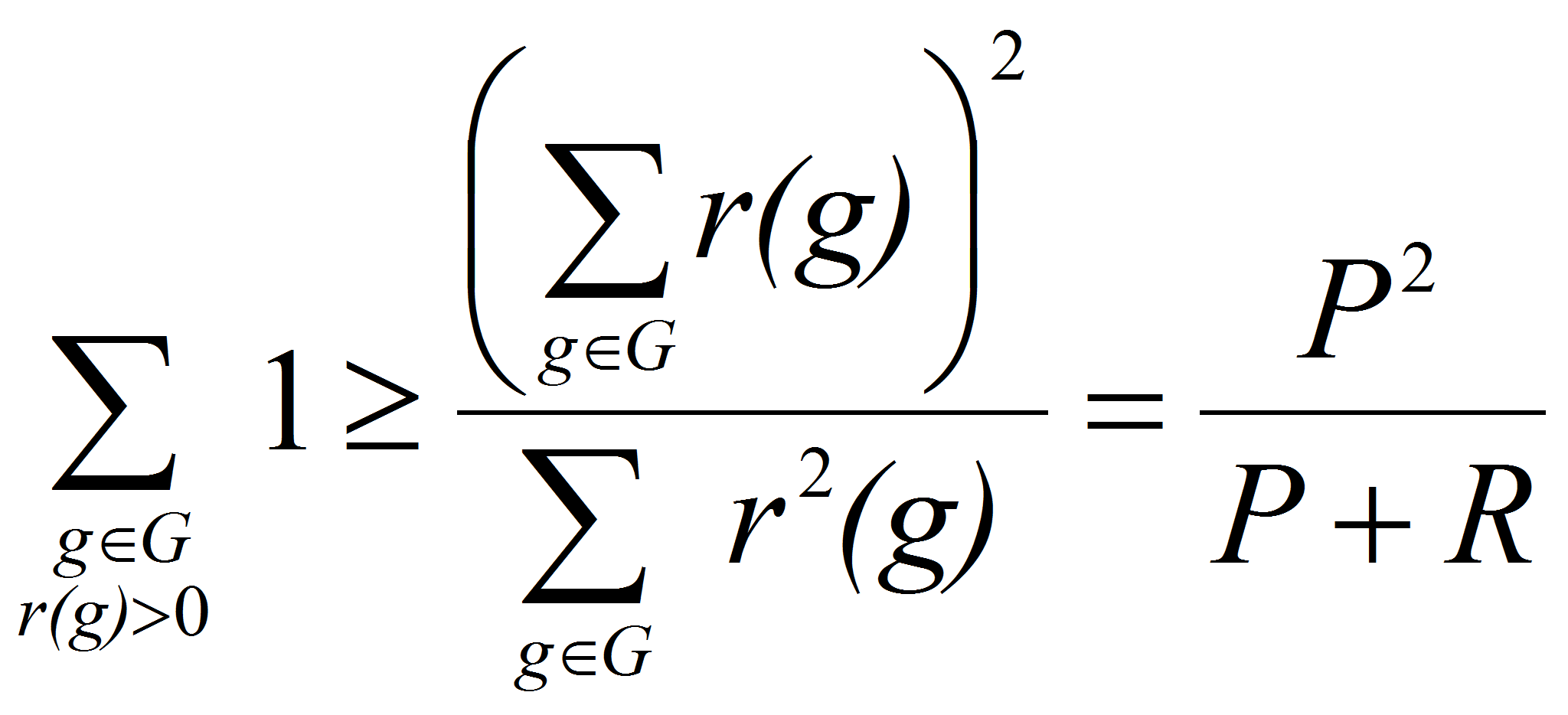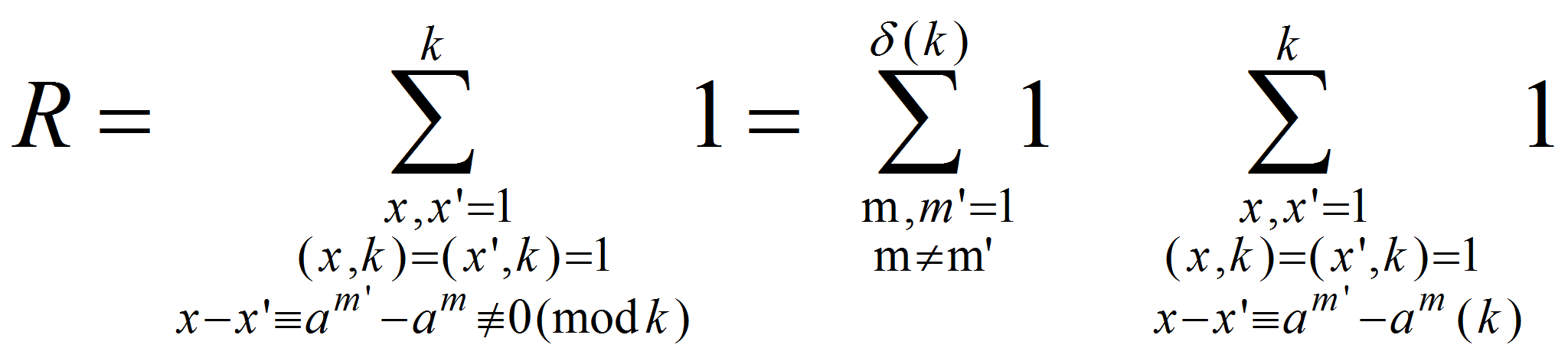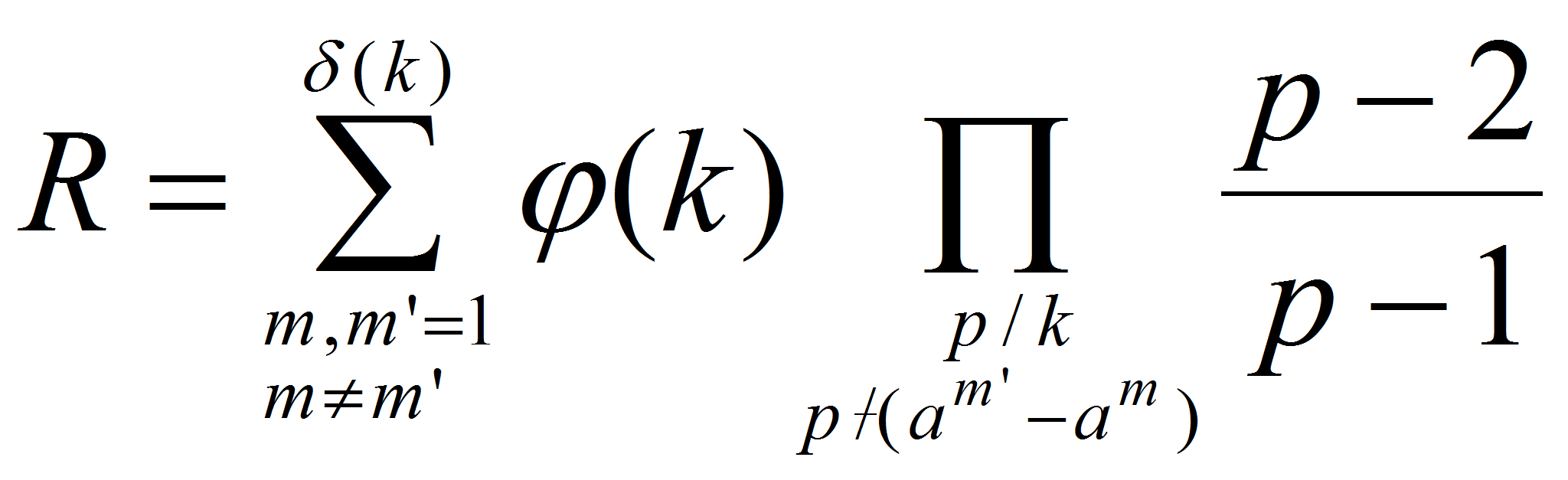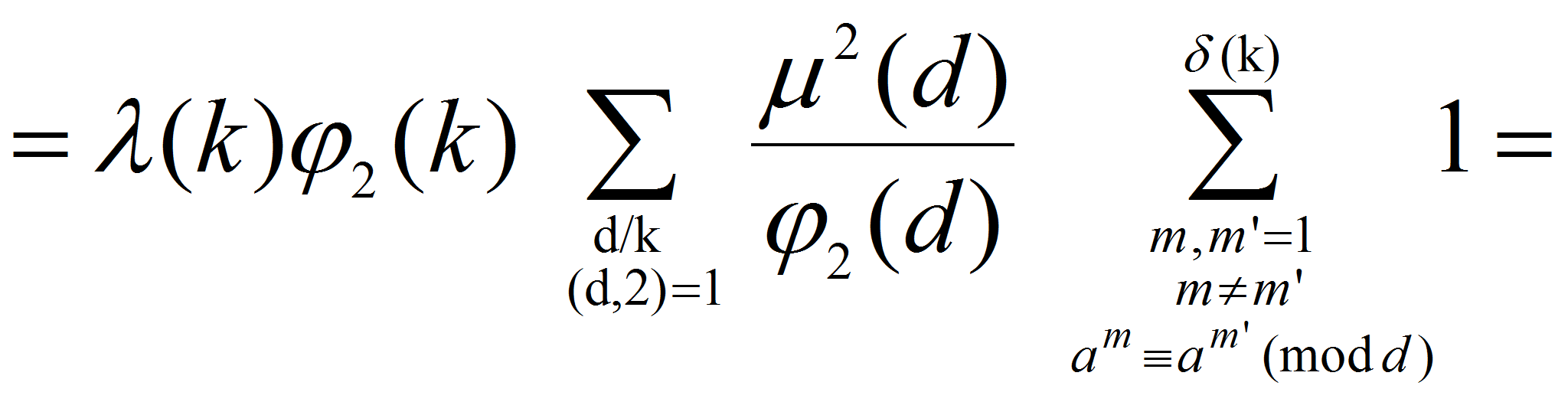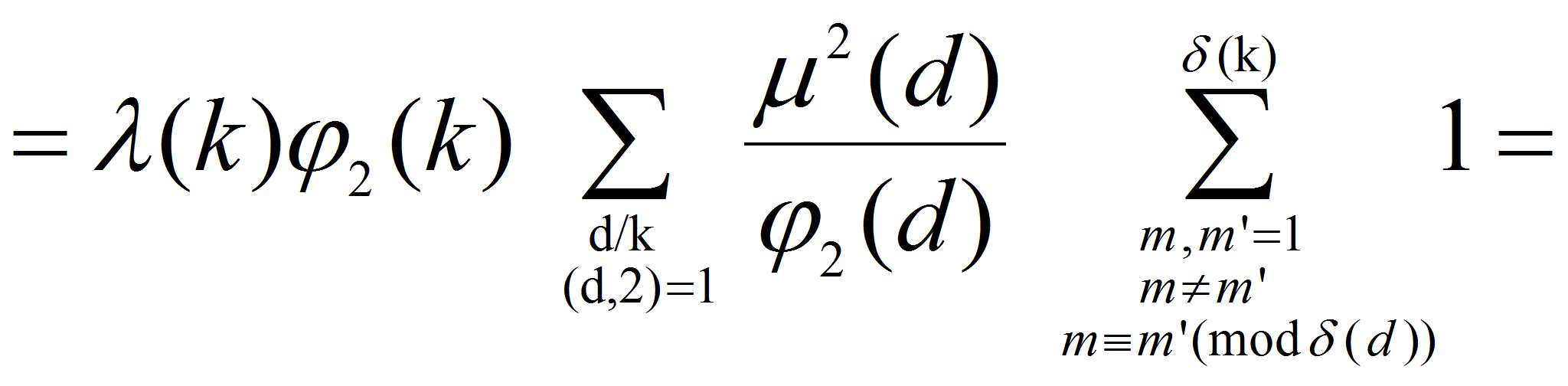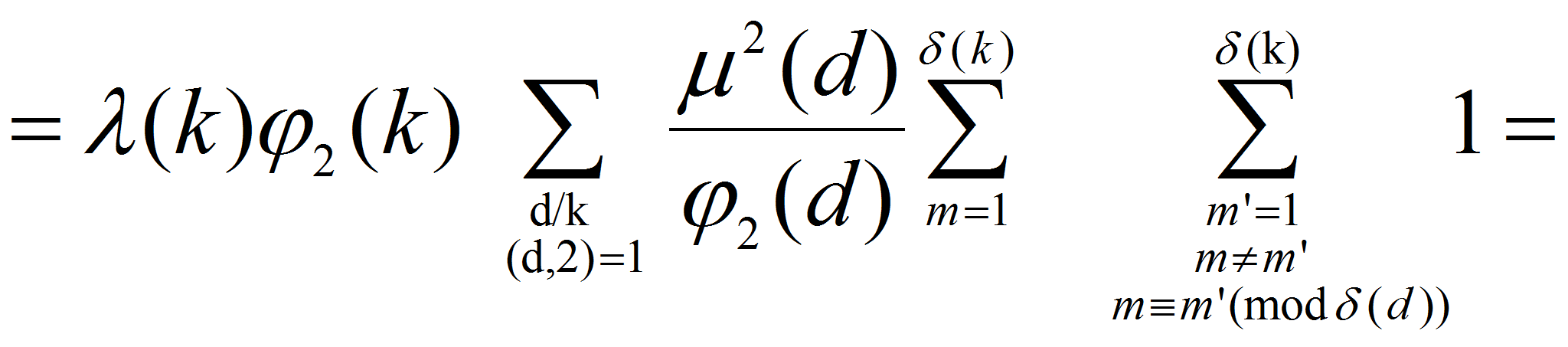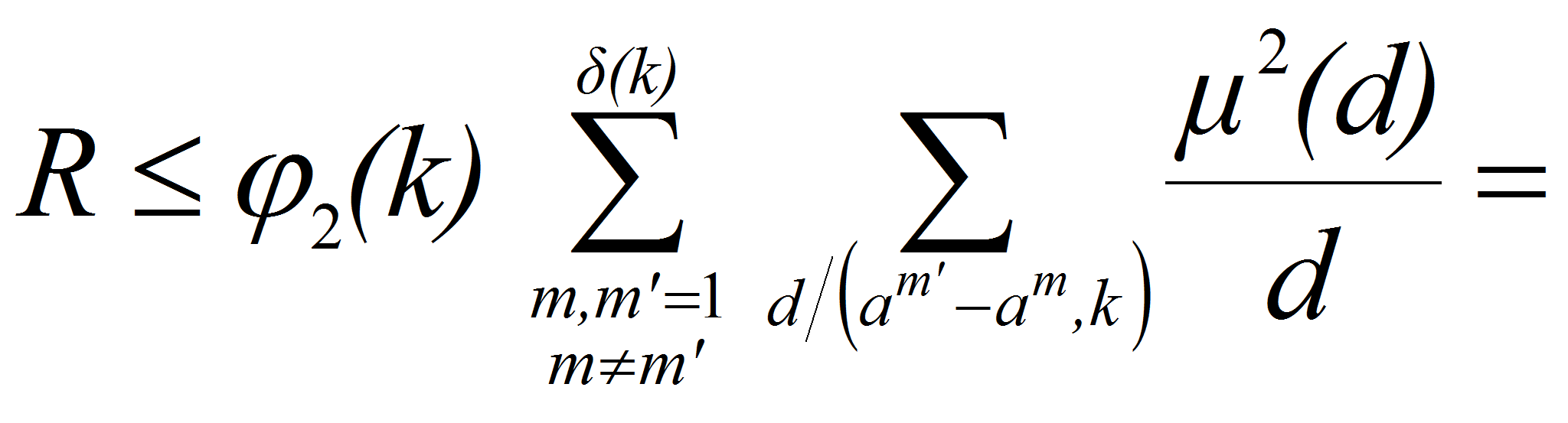Рассматриваются
задачи о сложении классов вычетов по растущему модулю. В частности,
получены условия, при которых плотность классов вычетов, представимых
в виде суммы двух классов из заданных множеств, положительна, то есть
число представимых классов по модулю
![]() больше,
чем
больше,
чем
![]() ,
где
,
где
![]() − положительная
константа. Устанавливается, что представление классов вычетов по
модулю
− положительная
константа. Устанавливается, что представление классов вычетов по
модулю
![]() в
виде суммы двух примитивных классов вычетов можно рассматривать как
аналог бинарной проблемы Гольдбаха для группы
в
виде суммы двух примитивных классов вычетов можно рассматривать как
аналог бинарной проблемы Гольдбаха для группы
![]() .
Получена точная формула для числа представлений натурального числа
.
Получена точная формула для числа представлений натурального числа
![]() в виде суммы двух примитивных классов по модулю
в виде суммы двух примитивных классов по модулю
![]() .
.
Problems about addition of classes of deductions on the growing module are considered. In particular, the following conditions are received at which the density of classes of deductions, representable in the form of the sum of two classes from the set sets, is positive, that is the number of representable classes on the module k is more than сk, where с – is a positive constant. It is established that representation of classes of deductions on the module k in the form of the sum of two primitive classes of deductions can be considered as analogue of a binary problem of Goldbah for group zk. The exact formula is received for number of representations of natural number n in the form of the sum of two primitive classes on the module k.
Пусть
![]() - натуральное число. Мы будем рассматривать вопросы о представлении
класса вычетов по модулю
- натуральное число. Мы будем рассматривать вопросы о представлении
класса вычетов по модулю
![]() в виде суммы нескольких классов вычетов по модулю
в виде суммы нескольких классов вычетов по модулю
![]() ,
принадлежащих некоторым заданным подмножествам группы
,
принадлежащих некоторым заданным подмножествам группы
![]() Например, так как все простые числа за исключением простых делителей
Например, так как все простые числа за исключением простых делителей
![]() находится в примитивных классах вычетов по модулю
находится в примитивных классах вычетов по модулю
![]() ,
причем имеются в каждом примитивном классе вычетов по модулю
,
причем имеются в каждом примитивном классе вычетов по модулю
![]() ,
то вопрос о представлении классов вычетов по модулю
,
то вопрос о представлении классов вычетов по модулю
![]() в виде суммы двух примитивных классов вычетов можно рассматривать как
аналог бинарной проблемы Гольдбаха для группы
в виде суммы двух примитивных классов вычетов можно рассматривать как
аналог бинарной проблемы Гольдбаха для группы
![]()
В отличие от классической
проблемы Гольдбаха этот ее аналог для группы
![]() решается полностью.
решается полностью.
Пусть
![]() - целое число, обозначим через
- целое число, обозначим через
![]() - число представлений
- число представлений
![]() в виде суммы двух примитивных вычетов по модулю
в виде суммы двух примитивных вычетов по модулю
![]() ,
т.е. число решений сравнения
,
т.е. число решений сравнения
![]() в примитивных вычетах
в примитивных вычетах
![]() и
и
![]() Имеем:
Имеем:
где
![]() - число решений сравнения
- число решений сравнения
![]() В силу мультипликативности функции
В силу мультипликативности функции
![]() по первому аргументу, отсюда следует;
по первому аргументу, отсюда следует;
Из
определения функции
![]() ,
следует, что
,
следует, что
Поэтому
Таким
образом, мы получили точную формулу для числа представлений целого
числа
![]() в виде суммы двух примитивных вычетов по модулю
в виде суммы двух примитивных вычетов по модулю
![]() .
Из нее в частности следует, что при нечетном
.
Из нее в частности следует, что при нечетном
![]() такое представление существует для любого
такое представление существует для любого
![]() ,
а при четном
,
а при четном
![]() указанное представление допускает все четные
указанное представление допускает все четные
![]() и только они.
и только они.
Более сложные задачи получаются при рассмотрении аналогов известных задач о представлении натуральных чисел в виде суммы двух слагаемых, одно из которых является простым числом, а другое принадлежит некоторой редкой последовательности. Первой из таких задач является задача о представлении натуральных чисел в виде суммы простого числа и степени некоторого заданного целого числа, рассмотренные Н.П.Романовым [1] ,который доказал, что множество представимых чисел имеет положительную асимптотическую плотность.
Мы докажем, что некоторый
аналог теоремы Романова справедлив на группе
![]() .
.
Отметим прежде всего, что тождество Романова, на котором основано доказательство его теоремы, можно обобщить на любую аддитивную группу.
Пусть
![]() - аддитивная абелева группа,
- аддитивная абелева группа,
![]() и
и
![]() - какие-либо подмножества группы
- какие-либо подмножества группы
![]() ,
,
![]() - некоторое конечное множество пар
- некоторое конечное множество пар
![]() где
где
![]() Для каждого
Для каждого
![]() обозначим через
обозначим через
![]() - число представлений элемента
- число представлений элемента
![]() в виде суммы
в виде суммы
![]() где
где
![]() Тогда
Тогда
Это и есть
аналог тождества Романова для группы
![]() .
Применим его к случаю когда
.
Применим его к случаю когда
![]() множество примитивных классов по модулю
множество примитивных классов по модулю
![]()
![]() множество вычетов по модулю
множество вычетов по модулю
![]() чисел
чисел
![]() где
где
![]() - заданное целое число взаимно простое с
- заданное целое число взаимно простое с
![]() (таким образом, в данном случае
(таким образом, в данном случае
![]() ),
),
![]()
Заметим
для дальнейшего, что наряду с тождеством Романова для аддитивной
группы
![]() справедливы также аналоги неравенств Романова-Шнирельмана и
Романова-Эрдеша. Действительно, в силу неравенств Коши
справедливы также аналоги неравенств Романова-Шнирельмана и
Романова-Эрдеша. Действительно, в силу неравенств Коши
Отсюда и из тождества Романова следует
(аналог неравенства Романова-Шнирельмана).
Далее,
(аналог неравенства Романова-Эрдеша).
Подсчитаем
величины
![]() и
и
![]() в интересующем нас случае. Так как общее число примитивных классов по
модулю
в интересующем нас случае. Так как общее число примитивных классов по
модулю
![]() равно
равно
![]() а число различных вычетов чисел
а число различных вычетов чисел
![]() по модулю
по модулю
![]() равно
равно
![]() -показателю
числа по модулю
-показателю
числа по модулю
![]() ,
то
,
то
![]()
Так как
![]() пробегает вместе с
пробегает вместе с
![]() приведенную систему вычетов по модулю
приведенную систему вычетов по модулю
![]() то для подсчета внутренней суммы можно использовать полученный ранее
результат о представлении целых чисел суммой двух примитивных вычетов
по модулю
то для подсчета внутренней суммы можно использовать полученный ранее
результат о представлении целых чисел суммой двух примитивных вычетов
по модулю
![]() Получаем:
Получаем:
Отметим,
что если
![]() и
и
![]() одновременно четны то при
одновременно четны то при
![]() и при
и при
![]() соответствующие слагаемые равны 0, а слагаемые, отвечающие остальным
значениям
соответствующие слагаемые равны 0, а слагаемые, отвечающие остальным
значениям
![]() и
и
![]() ,
отличны от нуля (так как в них разность
,
отличны от нуля (так как в них разность
![]() является четной &#﴿;.
является четной &#﴿;.
Если же
![]() и
и
![]() не являются одновременно четными, то все слагаемые положительны ввиду
четности разности
не являются одновременно четными, то все слагаемые положительны ввиду
четности разности
![]() при нечетном
при нечетном
![]() .
.
Введем обозначение
Тогда,
если
![]() и
и
![]() не являются одновременно четными, то
не являются одновременно четными, то
Случай,
когда
![]() и
и
![]() одновременно четны, рассматривается аналогично. Отсюда вытекает
следующая оценка сверху для
одновременно четны, рассматривается аналогично. Отсюда вытекает
следующая оценка сверху для
![]()
В силу
сходимости ряда Романова последняя сумма ограничена константой,
зависящей только от
![]() так что
так что
Отсюда и
из неравенства Романова-Шнирельмана для группы следует: Число классов
вычетов по модулю
![]() ,
представимых в виде суммы примитивного класса и класса, порожденного
некоторой степенью числа
,
представимых в виде суммы примитивного класса и класса, порожденного
некоторой степенью числа
![]() больше чем
больше чем
Так как
то отсюда следует
Теорема
1.
Пусть
![]() - число классов вычетов по модулю
- число классов вычетов по модулю
![]() ,
представимых в форме суммы примитивного класса и вычета некоторой
степени числа
,
представимых в форме суммы примитивного класса и вычета некоторой
степени числа
![]() по модулю
по модулю
![]() Тогда справедливо неравенство
Тогда справедливо неравенство
где
![]() - положительная константа.
- положительная константа.
Поскольку
общее число классов вычетов по модулю
![]() равно
равно
![]() ,
это означает, что множество классов вычетов по модулю
,
это означает, что множество классов вычетов по модулю
![]() ,
представимых в указанным образом имеет положительную асимптотическую
плотность при
,
представимых в указанным образом имеет положительную асимптотическую
плотность при
![]()
Литература:
Romanov N.P Uber einige Starze der additiven Zahlentheorie, Math. Ann.109 (1934).668-678.
Selberg S. A. generalization of a theorem of Romanoff, Kong. Norske vid.Selsc. For handl. 35,17 (1962),91-95.
Файнлейб А.С., Оразов М. Бинарные аддитивные задачи с показательной функцией. Литовский математический сборник.1978.№4. 187-198.
Оразов М. Аддитивные задачи с редкими последовательностями, канд. диссертация, Чарджоу,1982.