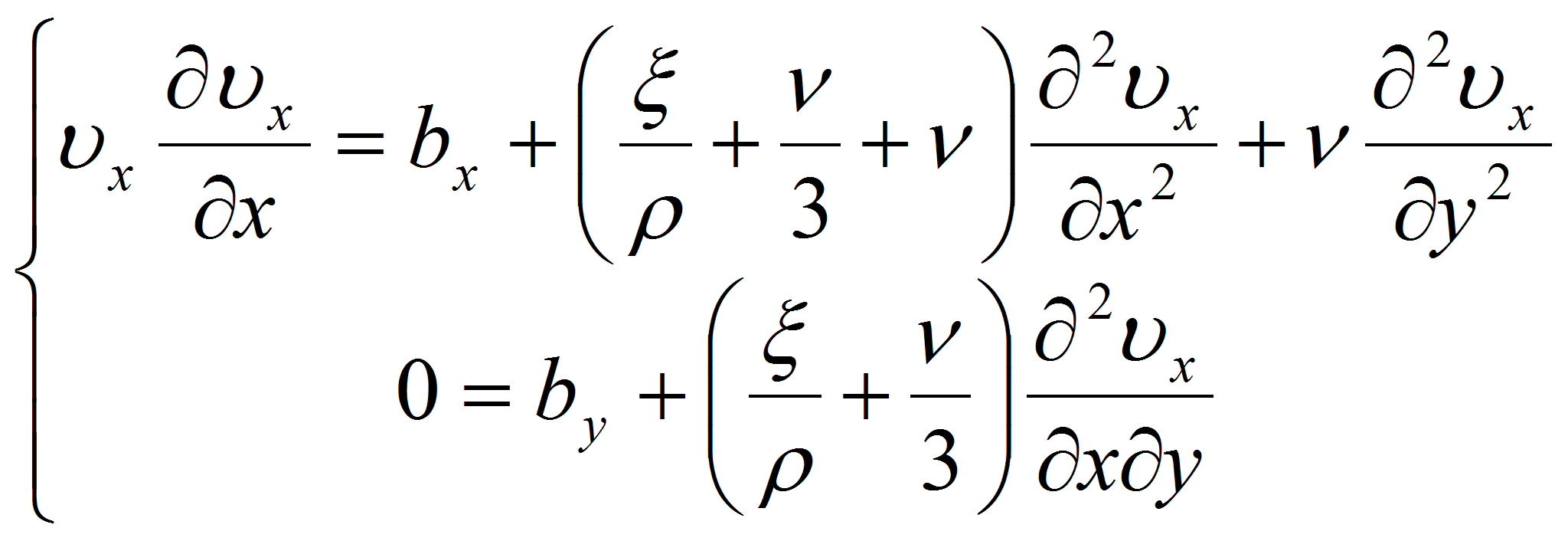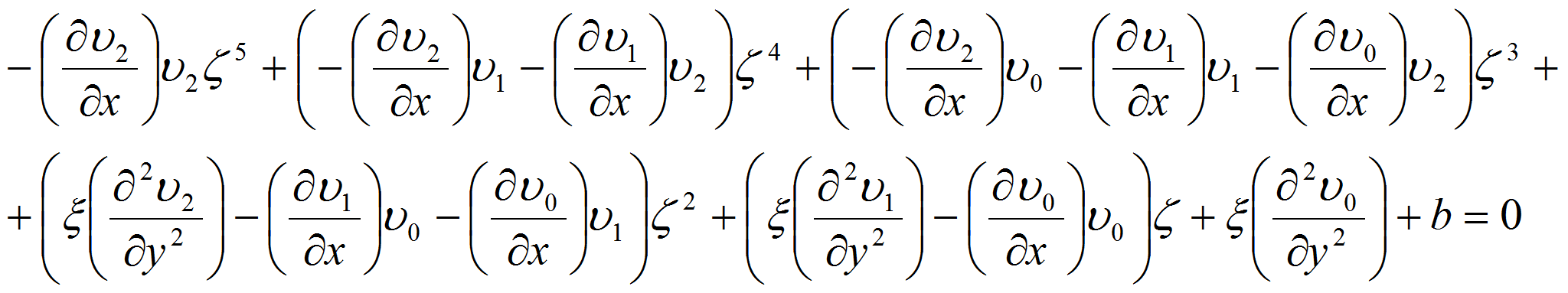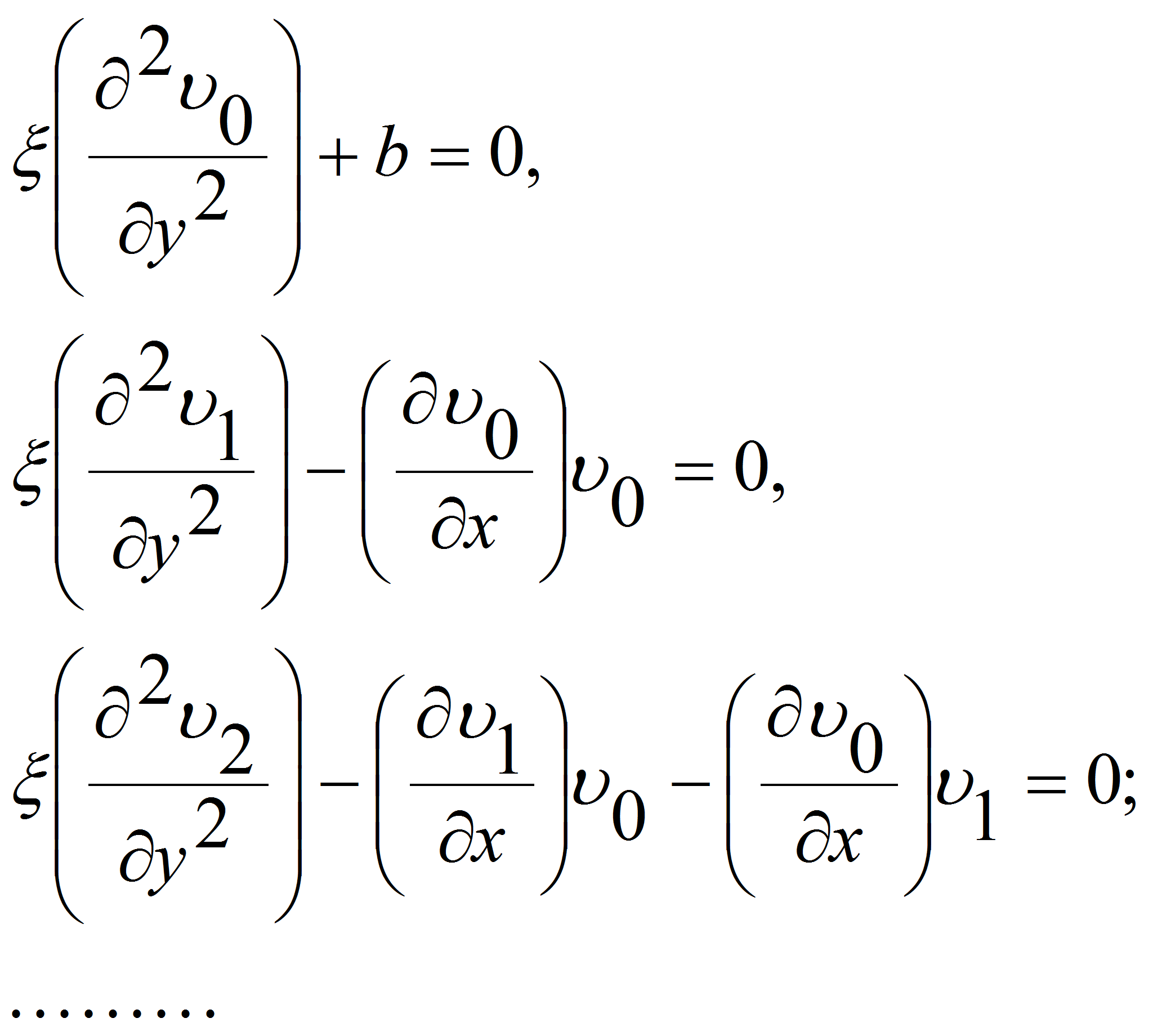Найдено точное решение одной модели движения жидкости в канале прямоугольной формы. Это решение может быть использовано для проверки работоспособности численных алгоритмов.
Постановка задачи о стационарном течении вязкой сжимаемой жидкости в канале прямоугольной формы.
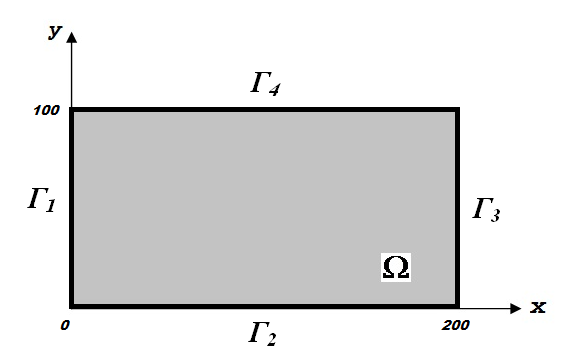
Пусть в
области
![]() с границами
с границами
![]() протекает вязкая сжимаемая жидкость. Ширина канала слева, куда
втекает жидкость, имеет размер
протекает вязкая сжимаемая жидкость. Ширина канала слева, куда
втекает жидкость, имеет размер
![]()
Рисунок 1 – Область определения задачи
Для вывода уравнений, описывающих течение, примем за основу уравнение движения в напряжениях [1]:
где
![]() -
тензор напряжений в жидкости,
-
тензор напряжений в жидкости,
Для замыкания (1) запишем определяющее соотношение, представляющее собой зависимость между девиаторами напряжений и деформаций или скоростей деформаций. Вид конечных уравнений будет определяться выбором определяющего соотношения.
Определяющее выражение для
![]() имеет следующий вид:
имеет следующий вид:
-
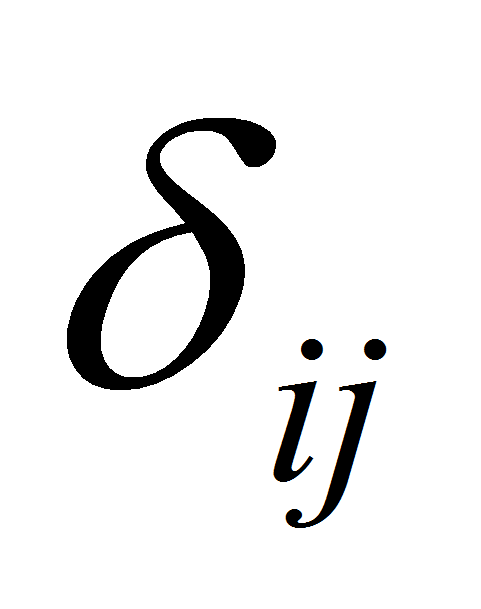 - символ Кронекера,
- символ Кронекера,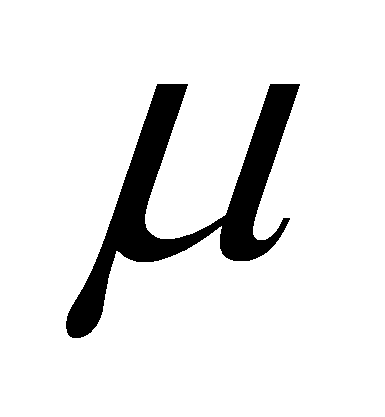 - динамический
коэффициент вязкости,
- динамический
коэффициент вязкости, - объёмный коэффициент
вязкости,
- объёмный коэффициент
вязкости,- р – постоянная, имеющая размерность давления.
Система уравнений движения (1) не содержит давление. Для вязкой сжимаемой жидкости используется дополнительное соотношение (2), в которое давление входит явно.
Давление не связано с деформациями и не совершает работу при движении жидкости. Это не позволяет использовать вариационные принципы аналитической динамики для получения разрешающих уравнений и граничных условий в давлениях. Таким образом, будем рассматривать модель жидкости со специальным определяющим уравнением, связывающим все компоненты напряжений со скоростями деформаций:
Заметим, что для реальных
жидкостей [2] давление намного больше касательных напряжений, а
дивергенция скорости мала. Поэтому в уравнении (3) коэффициент
![]() ,
определяющий давление, должен быть намного больше коэффициента
вязкости
,
определяющий давление, должен быть намного больше коэффициента
вязкости
![]() .
.
Подставив определяющее
соотношение в уравнение движения (1), и воспользовавшись определением
тензора скоростей деформации в виде
![]() ,
получим уравнения:
,
получим уравнения:
-
или
Целью гидродинамического расчёта является нахождение полей скоростей. Плотность и вязкость, входящие в уравнения, считаются известными.
С математической точки зрения, полученные уравнения (4), (5) относятся к классу нелинейных дифференциальных уравнений в частных производных второго порядка. Их нелинейность, обусловленная наличием конвективных членов ускорения, приводит к вычислительным трудностям при решении [3]. Поэтому поставим задачу в таком виде, чтобы можно было сохранить не все конвективные члены и не все члены, учитывающие вязкость.
Аналитический метод решения одно- и двумерной задачи.
Рассмотрим одномерную модель течения вязкой сжимаемой жидкости. Движение жидкости в канале (рисунок 1) установившееся [4], следовательно, все производные по времени равны нулю. Так как модель одномерная, то равны нулю и компоненты скорости по осям Y, Z. Таким образом, исходное уравнение с граничными условиями будет иметь вид:
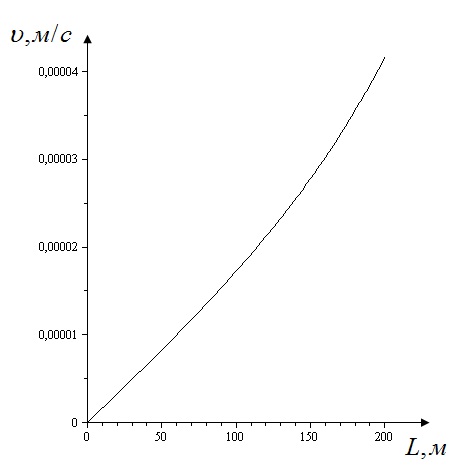
- Учитывая граничные условия, находим С1 , С2 и подставляем их в решение. Таким образом, точное решение имеет вид:
Рисунок 2 – Распределение скорости по длине канала
Рассмотрим
двумерную модель течения вязкой сжимаемой жидкости. Предположим, что
течение плоское, т.е.
![]() .
Тогда имеем:
.
Тогда имеем:
В результате требуется
решить в указанной области (рисунок 1) уравнение движения жидкости
(9) со следующими граничными условиями:
![]()
![]()
![]()
![]()
Введём параметр в задачу
[5]. Строить решение будем в виде суммы ряда по степеням малого
параметра
![]() :
:
Подставляя выражение (10) в
(9) и раскрывая скобки, получаем после группировки членов с
одинаковыми степенями
![]() :
:
Приравнивая нулю
коэффициенты при одинаковых степенях
![]() ,
получаем последовательность линейных краевых задач:
,
получаем последовательность линейных краевых задач:
Решив все уравнения (11) с
учётом граничных условий и подставив выражения для
![]() ,
,
![]() ,
,
![]() в (10), получаем искомое решение двумерной задачи. Так, при
сохранении трех слагаемых ряда (10) имеем:
в (10), получаем искомое решение двумерной задачи. Так, при
сохранении трех слагаемых ряда (10) имеем:
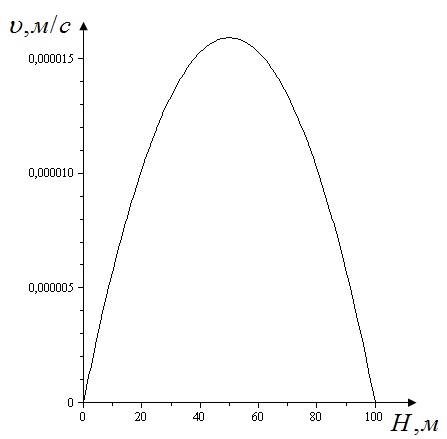
Рисунок 3 – Распределение скорости по ширине канала
В результате получено распределение скорости по ширине канала (рисунок 3). Рассмотренная модельная задача одно- и двумерного течения вязкой сжимаемой жидкости может быть использована для тестирования численной схемы интегрирования уравнений (1).
- Литература:
Мейз Дж. Теория и задачи механики сплошных сред [Текст] / Дж.Мейз. – М.: ЛКИ, 2007. – 320 с.
Лойцянский Л.Г. Механика жидкости и газа [Текст] / Л.Г. Лойцянский. – М.: Наука, 1970. – 904 с.
Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика [Текст] / К.С. Басниев, Н.М. Дмитриев, Г.Д. Розенберг. – Ижевск: Институт компьютерных исследований, 2005. – 544 с.
Биркгоф Г. Гидродинамика [Текст] / Г. Биркгоф. – М.: ИЛ, 1963. – 244 с.
Ван-Дайк М. Методы возмущений в механики жидкости [Текст] / М. Ван-Дайк. - М.: Мир, 1967. – 296 с.