Биангулярная система координат



В данной статье исследуется биангулярная система координат, а также изучается её связь с другими координатами, а также рассматриваются примечания к данной системе координат. При написании работы были использованы методы математического анализа, аналитической геометрии, векторного и тензорного анализа.

Ключевые слова: биангулярные, система координат, методы, связи, отношения, функции, углы.

This article explores the biangular coordinate system, as well as examines its relationship with other coordinates, and also discusses the notes to this coordinate system. When writing the work, the methods of mathematical analysis, analytical geometry, vector and tensor analysis were used.

Keywords: biangular, coordinate system, methods, connections, relationships, functions, angles.

Системы координат — это методы описания местоположения точек в пространстве. Двумя самыми популярными системами в двух измерениях являются декартовы (или прямоугольные) координаты и полярные координаты. Первая описывает координату, используя две точки (x и y), а последняя полагается на одну точку и один угол (r и θ). Естественным преимуществом другой системы является то, что каждое местоположение (точка P) определяется с использованием двух углов, и . Эта система представляет собой биангулярную систему координат (рис. 1) [1].

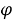
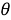
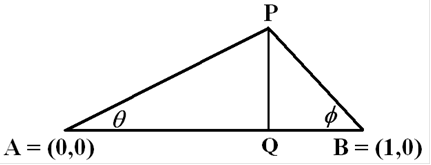
Рис. 1. Биангулярные координаты.

Рассмотрю две точки и в плоскости . Назову эти точки полюсами и ось проведенную через и — полярной осью. означает биангулярные координаты точки , образованной через пересечение двух лучей в точке , один выходит из точки под углом

(измеряется против часовой стрелки) от полярной оси , а другой луч — от точки под углом (измеряется по часовой стрелке) от полярной оси [2].

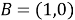
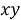
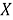
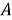
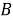
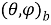
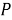
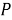
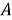
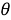
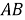
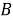
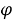
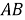
Попробуйте сами, держа руки вертикально вверх перед собой и позволяя локтям быть полюсами (рис. 2). Держа локти на месте, двигайте предплечьями в плоскости параллельно к фронтальной части тела. Ваши предплечья представляют собой лучи от полюсов, каждые из которых создают угол, один из точки и один из точки , и пересечение этих лучей является биангулярной координатой или точкой , описываемой этими углами — левая рука образует угол, , с горизонталью от точки , а правая рука образует угол,

, с горизонталью от точки .

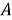
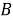
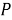
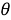
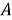
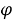
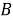
Держите свои предплечья горизонтально, т. е. и (рис. 2), а затем увеличивайте углы в одном темпе. Какая кривая описывается пересечениями ваших рук? [3]

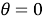
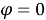
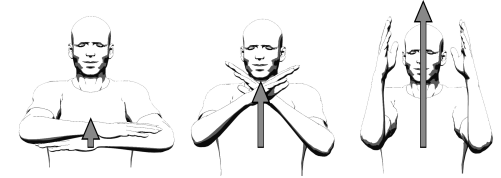
Рис. 2. Движения руками как биангулярные связи .

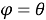
Затем начните с горизонтально расположенного левого предплечья, , а правое предплечье вертикально,

(рис. 3). Уменьшайте угол с той же скоростью, что и увеличиваете . Какая кривая описывается пересечением предплечий в этот раз? Вы «чувствуете» или «видите» ?

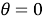
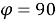
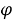
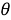
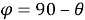
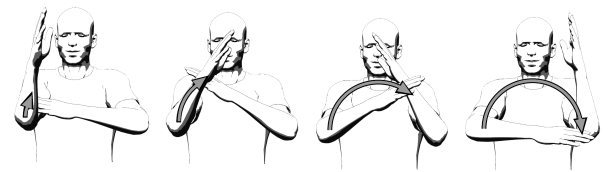
Рис. 3. Движения руками как биангулярные связи

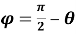
Изучение биангулярных координат имеет интересную историю, предлагает изучающим ее богатую атмосферу, в которой изучаются тригонометрия, геометрия и функции, а также позволяет задать вопросы «что если» и обнаруживать закономерности, отношения и связи, а также приводит к их пониманию.

Примечание к вычислениям в биангулярной системе. Для начала нужно преобразовать биангулярные координаты в прямоугольные координаты. Рисунок (4) демонстрирует, как найти прямоугольные координаты точки

: — длина отрезка , — длина отрезка , а — длина линейного сегмента . Точка находится на пересечении лучей выходящих из и .

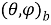
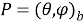
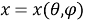
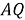
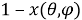
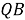
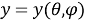
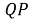
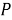
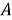
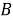
Рис. 4. Определение прямоугольных координат точки P, заданных биангулярными координатами

Если у меня есть отношения между и и скажем или , такую функцию или отношение называют биангалярным соотношением, и полученный график всех точек P определяется с помощью построения графика биангулярной связи [4].

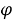
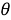
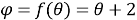
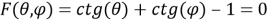
При изучении биангулярных координат и биангулярных связей в качестве вводного действия остается определение прямоугольных координат . Обычно эта проблема решается так. Опускается перпендикуляр от P до точки Q на полярной оси AB. В левом треугольнике , , и в правом треугольнике

: . Теперь, решая эти уравнения для и , а затем упрощая и используя тригонометрическое тождество для , получаем прямоугольное представление для точки :

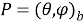
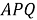
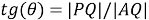
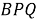
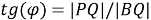
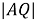
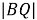
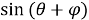
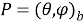
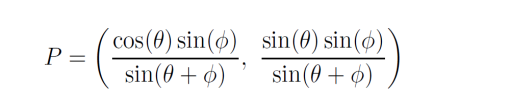
Скажем, для построения конкретной биангулярной связи или , мы используем параметрическую сюжетную процедуру для биангулярной функции или неявное построение графика для биангулярной связи, которое не является функцией.

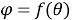
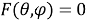
Вывод. Биангулярные координаты изящно описывают некоторые кривые, представления которых неуклюжи в других системах. Однако ценность их исследования заключается не столько в том, что эта система может выполнить, сколько в том, что она может рассказать нам о формах, функциях и системах координат в целом. Исследование биангулярных координат захватывает дух и дает радость математического открытия и изучения, поскольку эта система приятна и свежа в использовании.

Литература:

1. Baeumler H. W. Биангулярные координаты / H. W. Baeumler, M. A. Thesis // University of Buffalo, 1950.
2. Biggin T. О биангулярных координатах и расширении системы в трехмерном пространстве // Quarterly Journal of Pure and Applied Mathematics . 25(1891) 237–258.
3. Carnot L. N. M. Gґeomґetrie de Position / L. N. M. Carnot, J. B. M. Dupart // Paris, 1803.
4. Nelson D. Bipolar coordinates and plotters // PRIMUS, 4(1994) 77–83.
5. Walton W. О биангулярных координатах // Q. J. of Pure and App. Math . , 9 (1868) 47–57.