Кредитная модульная система регулирует многостороннюю деятельность университета: программу обучения, учебный план, расписание занятий, оценку знаний студентов, присуждение степеней, определение оплаты за учебу и т. д. Эта система дает возможность реально оценить деятельность преподавателя и студента, способствует определению нагрузок преподавателей и регулированию студенческой нагрузки, предоставляя возможность работать.
Ключевые слова: кредитная модульная система, самостоятельная работа, алгебра, теория чисел.
Кредитная модульная система регулирует многостороннюю деятельность университета: программу обучения, учебный план, расписание занятий, оценку знаний студентов, присуждение степеней, определение оплаты за учебу и т. д. Эта система дает возможность реально оценить деятельность преподавателя и студента, способствует определению нагрузок преподавателей и регулированию студенческой нагрузки, предоставляя возможность работать. Она обеспечивает свободу обучения, что соответствует рыночным экономическим отношениям. Внедрение единой системы учета учебной нагрузки в рамках кредит-система предполагает следующие шаги: введение модульной системы, предполагающей, что каждая дисциплина или модуль имеют фиксированную нагрузку. Нагрузка определяется исходя из:
− задач;
− результатов, которые должны быть получены;
− времени, которое необходимо затратить среднему студенту для их достижения.
− в каждом модуле или дисциплине выделяются определенные виды и формы обучения.
Преподаватель должен определить, какие формы и в каком объеме должны составлять структуру учебной нагрузки. В процессе обучения каждый студент зарабатывает кредиты, которые являются мерой трудоёмкости деятельности студента. Другими достоинствами этой системы являются: меньшее количество одновременно изучаемых дисциплин, индивидуализация педагогического процесса, практическая направленность, а также раскрытие творческих способностей студентов. В современных условиях кредитная система позволяет обучать более мобильных, компетентных и востребованных специалистов.
Кредитно-модульная система требует большого самоконтроля студента, т. к. ему самому приходится планировать свою индивидуальную образовательную программу, что зачастую представляет особую сложность для современной молодежи. Также в связи с перераспределением учебной нагрузки, произошло увеличение доли самостоятельной работы студентов, чем учащиеся явно не довольны. Преподавателями отмечается невозможность самостоятельного изучения студентами большого количества теоретического материала, даже невысокого уровня сложности. Внедрение кредитно-модульной системы обучения приводит к увеличению объема информации о ходе учебного процесса, ее обработки и хранения. В период межсессионной аттестации преподаватели заполняют ведомости, подготовленные деканатом, ведомости с результатами последней межсессионной аттестации представляются в деканат, деканат на основании ведомостей рейтинг-контроля по дисциплинам определяет интегральный рейтинг студента. Поэтому для успешного функционирования КМС необходимо обеспечить сопровождение учебного процесса соответствующей системой автоматизированного документооборота. Таким образом, кредитно-модульная система не является на данном этапе развития образования приоритетной технологией организации обучения в высшей школе. Однако, она, как и многие другие, имеет свои достоинства и недостатки, имеет реальные причины неработоспособности на практике.
Как известно, при кредитной технологии обучения сокращение объема аудиторной работы непосредственно повышает значение и статус самостоятельной работы студента. Если в традиционной системе обучения самостоятельная работа занимает одну третью часть от общей трудоемкости изучаемого курса обучения, то при кредитной системе обучения она составляет две трети части. Поэтому в условиях кредитной технологии самостоятельная работа студента становится одним из главных резервов повышения качества обучения и подготовки будущих специалистов.
Самостоятельная работа студентов делится на два вида:
− аудиторную,
− внеаудиторную.
Аудиторная самостоятельная работа студентов по дисциплине выполняется на учебных занятиях под непосредственным руководством преподавателя и по его заданию. Внеаудиторная самостоятельная работа выполняется студентами по заданию преподавателя, но без его непосредственного участия. Педагогическая ценность самостоятельной работы зависит также и от того, каким образом организована деятельность студентов. Формы организации самостоятельной деятельности студентов имеют важное воспитательное значение.
Самостоятельная работа в высшей школе является специфическим средством организации и управления самостоятельной деятельностью студентов в учебном процессе, средством самоорганизации и самодисциплины студентов в овладении необходимыми знаниями, умениями и навыками. Одним из основных факторов, которые влияет на профессионализм в будущем, является целенаправленное качественное образование. Самостоятельность — показатель успешности образования, которая необходимо в процессе, как обучения, так и в дальнейшем процессе преодоления учебных трудностей.
Само понятие «самостоятельной работы» подразумевает большой спектр работ и направления. Определенное значение зависит от того в каком значении используется термин «самостоятельный». В основном выделяют 3 значения данного слова:
− студент должен выполнять работу сам, без непосредственного участия педагога;
− от студентов требуются самостоятельные мыслительные операции, самостоятельное ориентирование в учебном материале;
− выполнение работы строго не регламентировано, студенту предоставляется свобода выбора содержания и способов выполнения задания.
Сейчас в вузах существуют две формы самостоятельной работы.
− традиционная, т. е. собственно самостоятельная работа студентов, выполняемая самостоятельно в произвольном режиме и времени, в удобные для студента часы, часто вне аудитории.
− аудиторная самостоятельная работа под контролем преподавателя, у которого в ходе выполнения задания можно получить консультацию.
Учебный процесс, основанный на самостоятельной работе студентов, можно разделить на два типа. Первое — это растущая роль самостоятельного обучения в учебном процессе. Реализация данного направления требует от учителей разработки методов и форм организации уроков, которые помогут обеспечить высокий уровень самостоятельности учащихся и повысить качество обучения. Второе — повысить активность учащихся во всех областях самостоятельной работы вне классной комнаты. В связи с этим следует признать, что самостоятельная работа студентов должна стать не только важной формой учебного процесса, но и его основой.
Решающая роль в организации самостоятельной работы принадлежит учителю, который должен работать не с «общим» учеником, а с его индивидуальными характеристиками, сильными и слабыми сторонами, способностями и наклонностями. Задача учителя — видеть и развивать в будущем лучшие качества студента как высококвалифицированного специалиста. Организация самостоятельной работы при изучении предмета должна представлять единство трех взаимосвязанных форм:
- Работа в классе под непосредственным руководством преподавателя;
- Работы выполняются вне классной комнаты;
- Творческая, в том числе исследовательская работа.
Наиболее подходящей формой оценки результатов учащихся по изучаемому предмету является система шкал. При разработке шкалы для оценки результатов самостоятельной работы студента необходимо разделить задачи для самостоятельной работы в соответствии с их уровнем сложности.
Рассмотрим, например, самостоятельную работу по модулю «Алгебраические системы» из курса алгебра и теории чисел. Эти задания предназначены для студентов с минимальными знаниями по модулю. Он состоит из 30 вариантов:
1. Задана
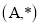
Варианты:
а) Найти нейтральный элемент в соответствии с данной операцией
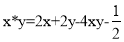
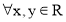
б) Найти нейтральный элемент в соответствии с операцией вида
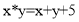
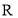
с). Найти нейтральный элемент в соответствии с приложением
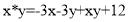
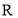
2. Дана
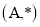
Варианты:
а) Найти симметричный элемент до -4 в соответствии с операцией * в форме
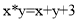
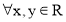
б) Найти элемент, симметричный 2, согласно операции * в форме
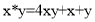
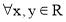
в) Найти симметричный элемент в соответствии с заданной * операцией
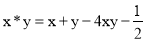
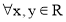
3. Заявка на набор
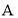
Варианты:
а)
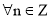
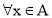
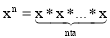
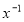
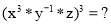
|
* |
х |
y |
z |
t |
|
х |
t |
х |
y |
z |
|
y |
х |
y |
z |
t |
|
z |
y |
z |
t |
х |
|
t |
z |
t |
х |
y |
б) Найти симметричный элемент
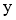
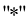
|
* |
х |
y |
z |
t |
|
х |
t |
х |
y |
z |
|
y |
х |
y |
z |
t |
|
z |
y |
z |
t |
х |
|
t |
z |
t |
х |
y |
в) Если
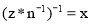
|
* |
х |
y |
z |
t |
к |
|
х |
z |
t |
к |
х |
y |
|
y |
t |
к |
х |
y |
z |
|
z |
к |
х |
y |
z |
t |
|
t |
х |
y |
z |
t |
к |
|
к |
y |
z |
t |
к |
х |
Теперь составим задания для студентов со средними знаниями по модулю. Эти задачи отличаются от вышеупомянутой задачи уровнем сложности:
1. Докажите, что следующие множества образуют аддитивную группу:
Варианты:
а);
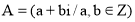
б);
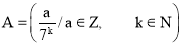
с).
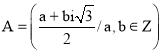
2. Докажите, что следующие множества образуют мультипликативную группу:
а);
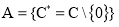
б);
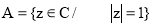
с).
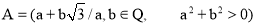
3. Докажите, что следующие множества образуют кольцо;
а)
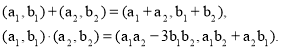
б);
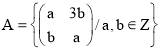
с)
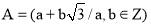
4. Докажите, что следующие наборы образуют поле:
а)
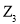
б)
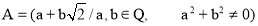
Следующие задания предназначены для студентов с большим количеством знаний, навыков и компетенций по всему модулю. Они более сложные задачи, чем указанные выше:
1. Объясните каждый из типов отражений с примерами.
2. Установить гомеоморфизм между следующими алгебрами:
а)
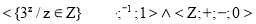
б)
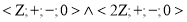
3. Установите изоморфизм между следующими алгебрами:
а)
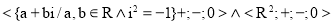
б)
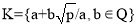
Установите изоморфизм между полями.
4. Докажите следующее.
а)
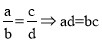
б)
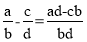
5. Поле и тело. Обоснуйте их разницу.
6. Приведите примеры коммутативного цикла.
7. Назовите нейтральный и симметричный элементы по отношению к действию композиции функций. Объясните примерами.
Хорошо известно, что студенты очень заинтересованы в том, чтобы знать, насколько хорошо они выполнили свою работу, в знании ценности их работы. Внедрение кредитной системы означает изменение философии образования, то есть переход от типа, который контролирует мастерство, к типу, который само регулируется — стимул.
Литература:
- Европейская система кредитов (ЕСПК). — Алматы — 2003. — 150 с.
- Ефимов A. B. Сборник задач по математике для втузов. 2006. — 250 с.
- Кредитная система высшего образования. — М.: Известия. — № 24 (57).
- Кубея Е. К. Особенности внедрения кредитной системы обучения в классическом университете. — Алма-ата, 2004. — 150 с.
- Буслюк Г. Е., Андреенко Р. Е., Колечёнок А. А. Модульное обучение. Минск: 2007. — 176 с.
- Кузнецова Е. И., Кравец А. Г. Моделирование кредитно-модульной структуры индивидуальной траектории обучения студента. Известия — 2009. Т. 6. — № 6.
- Курина, В. А. Внедрение кредитно-модульных систем в вузах. Вестник. Серия: психолого-педагогические науки. — 2011. — № 1. — С. 67–75.
- Гаргай, В. Б. Идея кредитно-модульного обучения: опыт надежд и поражений. Мир науки, культуры, образования. — 2010. — № 6. — С. 121.
- Хоботова, Э. Б. Возможности совершенствования кредитно-модульной технологии обучения Вестник — 2009. — № 45. — С. 7–9.







