Приступая к решению любой исследовательской задачи, мы не можем предсказать заранее результат решения. Поэтому набор методов, выбранных для достижения результата, в ходе решения может расширяться. Создание компьютерной программы, быстро обрабатывающей большой объём данных, — один из методов решения исследовательских задач, при этом необходимость использования этого метода может возникнуть на разных этапах решения. Иногда, начиная процесс исследования, мы даже не предполагаем, что в результате придём к необходимости программирования.
Часто, уже решённая, казалось бы, задача приводит к новым размышлениям и рождается новая задача для исследования. Такие «многосерийные» задачи уже несколько раз приводили к необходимости создания программы для компьютера, которая позволяет для заданного набора переменных быстро получать результаты вычислений.
Такие задачи обычно требуют от человека трудоёмких вычислений, полного перебора всех вариантов решения, а также учёта большого набора факторов, влияющих на решение. При создании алгоритма решения задача уже решается «в общем виде», что позволяет в более выгодном свете представить результаты своих изысканий, а также значительно глубже изучить исследуемые параметры и их влияние на полученные результаты.
Приведём несколько конкретных примеров, чтобы показать эффективность использования программированного решения таких задач. Причём в этих задачах программирование использовалось на разных этапах решения.
Задача для первоклассника
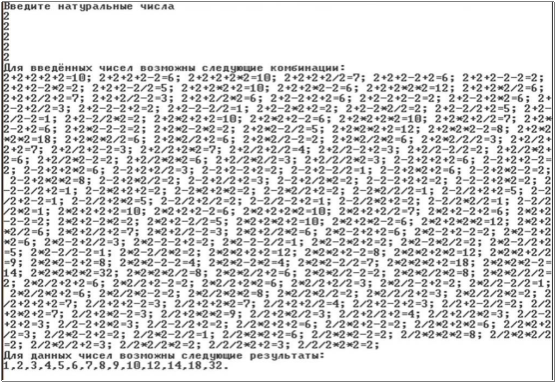
Все мы в детстве, едва научившись считать и понимать, что такое порядок действий, сталкивались с задачей про пять двоек: с помощью пяти двоек и знаков действий получить числа от 1 до 10.
Решение этой задачи не занимает много времени, но возникает вопрос — а какие вообще натуральные числа можно получить с помощью пяти двоек? Как доказать, что какое-либо число нельзя получить с помощью пяти двоек?
Необходимость использования компьютерных вычислений стала понятной уже на этапе формулировки задачи исследования: нужно создать программу, которая отберёт все натуральные числа, которые можно получить из пяти заданных однозначных чисел и знаков действий.
В результате использования программы мы получили полный набор выражений из пяти двоек, значения которых равны заданному натуральному числу.
Математическая модель кубика Рубика
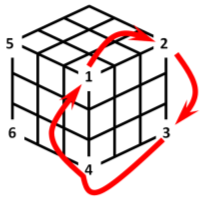
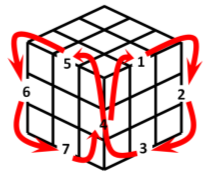
В течение четырёх лет участниками школьного научного общества изучалась всем известная головоломка — кубик Рубика. Было доказано, что собранное состояние кубика связано не со всеми возможными его состояниями. Если разобрать кубик и собрать его снова в произвольном порядке, то вероятность, что вы соберёте головоломку, равна 1/12. Доказано, что все состояния кубика можно разделить на 12 классов. Все состояния в одном классе связаны друг с другом и переводятся друг в друга вращением граней. При этом, как бы вы ни крутили грани, нельзя перейти из состояния, относящегося к одному классу, к состоянию, относящемуся к другому классу. Это можно сделать только намеренно или случайно повернув элемент головоломки в своём гнезде. При этом определить «на глаз» собирается ли головоломка из заданного состояния практически невозможно. Это требует учёта положения каждого элемента, а подвижных элементов немало — 8 угловых и 12 рёберных! Тем не менее, было доказано, что все 12 классов одинаковы по численности входящих в них состояний, но число этих состояний в одной группе безмерно велико и равно 11! 8! 3 8 2 12 =
= 43 252 003 274 489 856 000. Количество же самих классов определяется наличием трёх инвариантов, которые не изменяются при вращении граней кубика. Первый инвариант характеризирует количество неправильно установленных угловых кубиков и определяется числами m = 0; 1; 2. Второй инвариант характеризует количество неверно установленных рёберных кубиков и определяется числами n = 0; 1. Третий инвариант характеризует число транспозиций угловых и рёберных кубиков. Оно может совпадать по чётности или не совпадать, т. е. q = 0; 1. Отсюда и получается, что эти инварианты определяют 3 · 2 · 2 = 12 классов состояний кубика.
Получив все эти выводы, пришли к необходимости отнесения конкретного состояния кубика к тому или иному классу. В результате была создана математическая модель, которая с помощью 12 чисел описывает положение всех рёберных кубиков и с помощью 8 пар чисел описывает положение всех угловых кубиков.
Например, математическая модель кубика Рубика может выглядеть так: {3, -5, 4, 7, -2, -6, -1, 12, 10, -9, -8, 11}, {(3, 2), (5, 1), (4, 0), (7, 0), (2, 2), (6, 2), (1, 2), (8, 0)}.
На этом заключительном этапе исследования мы увидели, возможность использования компьютерных вычислений для быстрого определения класса, к которому относится кубик. В результате была создана программа, которая по математической модели состояния кубика определяет класс, к которому относится это состояние.
Вычисление периода последовательности состояний кубика Рубика при упорядоченном вращении его граней
Эта задача была поставлена и решена за два года. В начале своей работы было доказано, что при упорядоченном вращении граней кубика, если эти вращения начаты из собранного состояния, через определённое количество ходов кубик соберётся вновь, т. е. последовательность состояний кубика при упорядоченном вращении его граней представляет собой периодическую последовательность. Но как определить, через сколько повторений одной и той же комбинации вращения граней кубик соберётся вновь. Есть несколько вариантов решения задачи:
– можно вручную проверить, что, например, при вращении двух соседних граней в разные стороны, кубик соберётся через 63 пары вращений;
– можно рассмотреть, как ведут себя отдельные элементы кубика, и определить период вращения каждого задействованного элемента. Потом найти период самой последовательности вращений, как НОК всех периодов элементов.
Рассмотрим комбинацию поворотов, когда две соседние грани вращаются в разные стороны. Экспериментально было показано, что кубик собирается при этом за 63 пары поворотов.
|
|
|
|
Движение угловых кубиков описывается периодической последовательностью с периодом 9, т. е. через 9 повторов вращений все угловые кубики окажутся на своих местах |
Движение рёберных кубиков описывается периодической последовательностью с периодом 7, т. е. через 7 повторов вращений все рёберные кубики окажутся на своих местах |
То есть длина периода последовательности положений кубика Рубика равна НОК (9; 7) = 63, что и было получено экспериментально.
Оба этих решения трудоёмки и занимают большое количество времени. При этом не возникает общего решения, каждая новая комбинация требует новых, иногда достаточно сложных, расчётов. А для длинных комбинаций вращений найти период практически невозможно. Вот на этом-то этапе решения задачи и появилась идея решить задачу в общем виде, т. е. запрограммировать решение.
В результате была создана программа, которая рассчитывает количество повторов любой заданной последовательности вращений, которое необходимо выполнить, чтобы кубик вернулся в собранное состояние.
Подводя итог вышесказанному, можно с уверенностью утверждать, что программирование можно использовать при решении исследовательских задач. Причём оно может оказаться необходимым на любом этапе решения: как на этапе постановки задачи, так и в процессе решения, а также и для приведения в систему полученных результатов. Программирование является одним из методов достижения поставленной цели исследования.