Ключевые слова: налоги, кривая Лаффера, налогообложение.
Актуальность данной темы объясняется все большей заинтересованностью современных государств в фискальной политике и большому значению налогов в жизни национальных экономик. Для оптимального использования налогового потенциала экономики страны и получения максимальной выгоды экономистам необходимы различные инструменты и показатели для анализа макроэкономических факторов. Одним из таких показателей является кривая Лаффера. В статье показаны различные интерпретации кривой.
Концепция данной кривой Лаффера впервые была полностью сформулирована и опубликована в 1978 году в журнале Public Interest экономистом Джудом Ванниски. Кривая получила свое название в честь экономиста Артур Лаффер. [9]
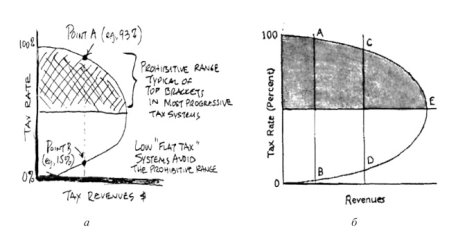
Рис. 1. a — изначальный вид кривой, предложенный Лаффером; б — модифицированная версия в статье Ванниски
Кривая Лаффера показывает взаимосвязь между налоговыми поступлениями и налоговыми ставками государства. По мере увеличения налоговых ставок налоговые поступления в бюджет будут сокращаться. Это связано с тем, что по мере увеличения налогов стимулы людей работать и инвестировать уменьшаются, следовательно, они зарабатывают меньше, меньше производят и потребляют, и налоговые поступления падают. Обратным эффектом является уменьшение налогового бремени, который приводит к увеличению сбережений, к росту инвестиций, занятости, выпуска продукций.
Объяснение наличия интервалов возрастания и убывания функции даны в работах П. Ю. Буряка и С. Л. Лондаря. Главная идея заключается в том, что при увеличении налоговой ставки происходит краткосрочное увеличение налоговых поступлений и последующее уменьшение поступлений в долгосрочном периоде из-за сокращения налоговой базы. Ситуация с уменьшением налоговой ставки диаметрально противоположенная. В долгосрочном периоде налоговые поступления уменьшаются, в долгосрочном-увеличиваются из-за увеличения налоговой базы. Наглядно это проиллюстрировано на рисунке 2. [2]
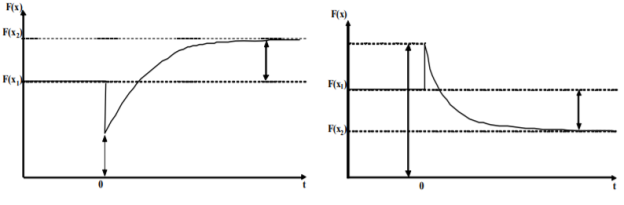
Рис. 2. Кривая Лаффера в координатах «налоговые поступления — время» а — при сокращении налоговой нагрузки; б — при повышении налоговой нагрузки
Изначально кривая изображалась в виде перевернутой колоколообразной функции, которая пересекает ось ординат в точках 0 % и 100 % (рисунок 1).
С момента публикации статьи про кривую Лафферта появилось много исследование на эту тему и множество доработок кривой. Среди отечественных экономистов этой темой занимались Ананиашвили, Е. В. Балацкого и другие. Среди западных ученых, уделивших внимание данной теме: Дж. Бьюкенен, Дж. Ванниски, П. Кругман. [5]
Большинство публикаций на эту тему можно поделить на две группы: те, кто строил кривую с помощью анализа теоретических сторон и те, определял внешний вид кривой учитывая экономико-математических моделей, задающих вид зависимости между налоговыми поступлениями и налоговой нагрузкой. Также стоит отметить отдельные виды кривой, где координатные плоскости задаются в непривычном виде: «налоговая нагрузка — время» или «налоговая нагрузка — налоговая база».
Рассмотрим вариации кривой в различных исследованиях наиболее известных авторов.
Рассмотрим крайние точки кривой Лаффера. Наличие крайних точек кривой является предположением, которое не имеет под собой объективного основания, так как если средняя ставка равна нулю, значит, что все налоги равны нулю. В этом случае мы не можем говорить о нулевых доходах государства, так как государство в этом случае не существует, ведь наличие налогообложения является необходимым условием существования государства. С другой стороны, 100 % налогообложение также не является условием нулевых доходов государства. Это опровергается марксисткой школой экономики и наличием социалистического опыта в мире. В данном случае мы не можем говорить в явно определенном на концах кривом Лаффера. Графическое изображение будет выглядеть как на рисунке 3, где T-размер налоговых поступлений, t-размер общих усредненных налоговых ставок. [1]
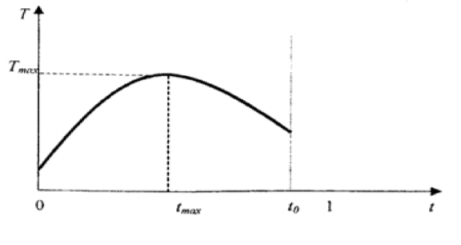
Рис. 3. Кривая Лаффера с учетом неопределенности крайних условий
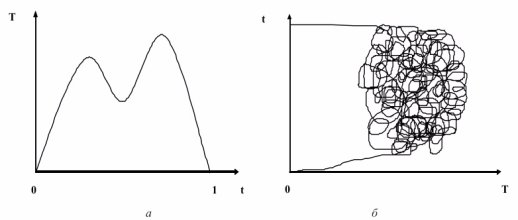
Рис. 4. Кривая Лаффера с несколькими точками максимума
Исследователи также уделяют внимание на то, что наличие одной критической точки на кривой Лаффера малообоснованно, а доказательство носит догматичный характер. [6] Вполне допустимо существование нескольких точек максимума. Это можно объяснить, к примеру, воздействием уровня налогообложения на стимулы людей к труду. Существует множество факторов, которые влияют на предпочтения граждан после повышения налогов: степень квалифицированности труда, полом, возрастом, уровнем образования и дохода. Одни люди после начнут усерднее трудиться или найдут дополнительный источник дохода (эффект дохода), другие же люди предпочтут досуг (эффект замещения). Так как эффект дохода и эффект замещения имеют разные степени эластичности и разные знаки, то при изменении налоговой ставки они будут оказывать совершенно разные последствия на рынок труда и тем самым на экономическую обстановку в стране и на уровень дохода бюджета. На рисунке 4 (а) представлен вариант кривой, предложенный британским экономистом Дэвидом Хендерсоном, на котором изображено 2 точки максимума. [8] Свою версию кривой предложил американский математик Мартин Гарднер, столкнувшись с многообразием вводных данных (рисунок 4 (б)). [7]
Также существуют работы, в которых в альтернативу множеству точек максимума ставиться отсутствие точки перегиба. Так как выше было описано, что граничные точки 0 % и 100 % не обязательно должны ровняться нулю, то можно сделать предположение, что зависимость налоговых поступлений от средней налоговой ставки монотонно возрастающая функция. Это возможно, например, при сильном увеличение уровня инфляции. Соответствующую кривую (рисунок 5) построил российский экономист Е. В. Балацкий.
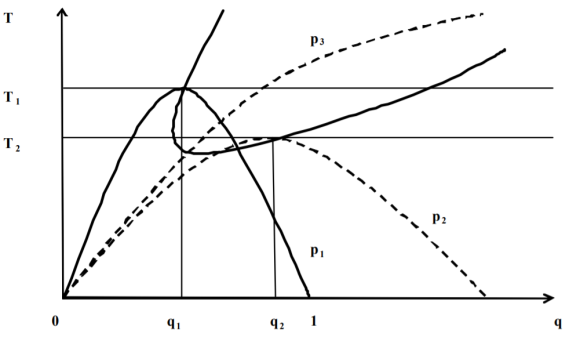
Рис. 5. Кривая Лаффера без точки перегиба
Существуют версии кривой, в которых учитывается немаловажный фактор-время. Необходимо придавать значение, в долгосрочном или краткосрочном периоде рассматривается кривая Лаффера. В работах В. П. Вишневского приводится анализ временного фактора. Повышение уровня налоговой нагрузки приведет к росту налоговых поступлений в бюджет в краткосрочном периоде, однако снижение нагрузки приведет в росту доходов в краткосрочном периоде. Эту закономерность хорошо видно на рисунке 6. [2]
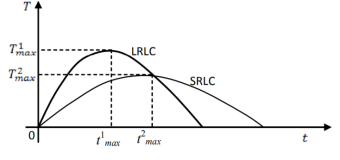
Рис. 6. Кривая Лаффера с учетом времени для долгосрочных (LRLC) и краткосрочных (SRLC) периодов
Дальнейшие усовершенствования кривой привели исследователей к рассмотрению не только налоговой ставки, но и налоговой базы. Так в 1984 г. В. П. Волобуев предложил усовершенствованный вид кривой. Данная кривая учитывает зависимость величину налоговой базы от налоговой ставки (рисунок 7). Вогнутая кривая на дополнительной координате показывает размер налоговой базы с учетом теневой экономики. Логически понятно, то с увеличением фискальной нагрузки количество предприятий и организаций будет уменьшаться. Кроме того, все больше предприятий и организаций будут применять методы уклонения от налогообложения и пользоваться инструментами теневой экономики. [4]
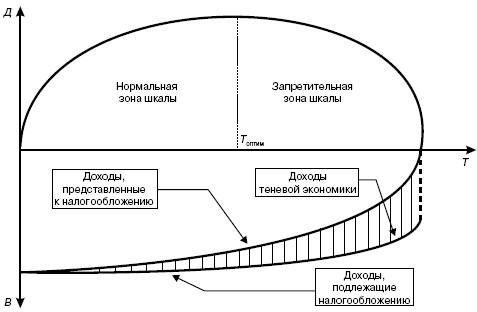
Рис. 7. Кривая Лаффера с учетом налоговой базы
На графике пунктиром обозначены доходы государства, потерянные из-за деятельности теневой экономики. Как видим эти доходы тем больше, чем больше налоговая ставка.
Проведенный анализ различных вариаций кривой Лаффера позволяет сделать вывод о том, что первоначальная модель, предложенная Лаффером подверглась коррекции и доработкам. Имеют место значительные теоретические допущения, которые предварительно необходимо учитывать при использовании кривой Лаффера как инструмент анализа.
Литература:
- Балацкий, Е. В., 1997в. Точки Лаффера и их количественная оценка. Мировая экономика и международные отношения, № 12
- Букач Б. А. Обоснование и анализ различных вариантов графической интерпретации кривой Лаффера //Вiсник СевНТУ. — 2012. — №. 130. — С. 30–38.
- Вишневский В. П., Липницкий Д. В. Оценка возможностей снижения налогового бремени в переходной экономике // Вопросы экономики. 2000. № 2. С. 107–116
- Волобуев В. П. Точки Лаффера и их количественная оценка // Мировая экономика и международные отношения. 1984. № 11. С. 119–125.
- Какаулина М. О. Графическая интерпретация кривой Лаффера с учетом налоговой «миграции» //Вестник УрФУ. Серия: Экономика и управление.—2017.—№ 3. — 2017. — №. 3. — С. 336–356.
- Макконнелл, К. Р. и С. Л. Брю, 1992. Экономикс: Принципы, проблемы и политика. Т.1. Москва, Республика.
- Gardner, M. (1981). Mathematical games. The Laffer curve and the otherlaughs in current economics. Scientific American.
- Henderson D. Limitation of the Laffer curve as a justification for tax // Cato Journal. 1981. Vol. 1, No. 1. P. 45–52.
- Wanniski, J. (1978). Taxes, Revenues, and the «Laffer Сurve». The Public Interest.







